Obsah

AP11, IN11 Zásobníkové automaty, Syntaktická analýza
Diskuze

AP11, IN11 Zásobníkové automaty, Syntaktická analýza

Zadání

(definice, převod bezkontextové gramatiky na zásobníkový automat)

(syntaktická analýza shora dolů a zdola nahoru, průběh analýzy daného slova)

Vypracování

Intuice zásobníkového automatu

Zásobníkový automat = PushDown Automaton = PDA

Na vstupní pásce je napsáno slovo (nad jistou vstupní abecedou) – lze z ní pouze číst, čtecí hlava se pohybuje pouze vpravo. Automat může na vrchol zásobníku ukládat symboly (z jisté abecedy) a ty následně číst – čte vždy jen vrchol zásobníku, přečtený symbol je odstraněn = systém LIFO (Last In First Out).

Formální definice

Definice 3.36. - PDA ¹⁾

Nedeterministický zásobníkový automat (PushDown Automaton, PDA) je sedmice $M = (Q, \Sigma, \Gamma, \delta, q_{0}, Z_{0}, F)$ , kde
• Q je konečná množina, jejíž prvky nazýváme stavy,
• $\Sigma$ je konečná množina, tzv. vstupní abeceda,
• $\Gamma$ je konečná množina, tzv. zásobníková abeceda,
• $\delta : (Q \times (\Sigma \cup{{\varepsilon}})\times \Gamma) \rightarrow P_{Fin}(Q \times \Gamma^{*})$ , tzv. (parciální) přechodová funkce (zápis $P_{Fin}(Q \times \Gamma^{*})$ značí množinu všech konečných podmnožin množiny $Q\times \Gamma^{*}$ – dvojice stav a řetězec symbolů zásobníkové abecedy),
• $q_{0} \in Q$ je počáteční stav,
• $Z_{0} \in \Gamma$ je počáteční symbol v zásobníku,
• $F \subseteq Q$ je množina koncových stavů.

$\delta(q_{0}, a, Z_{0}) = \{(q_{0}, AZ_{0})\}; Z_{0}$ … dno zásobníku, A … vrchol zásobníku, přidal se v tomto kroku
$\delta(q_{0}, c, A) = \{(q_{1}, A)\}$ … obsah zásobníku se nezměnil, pouze se přešlo do stavu q₁ $\delta(q_{1}, b, A) = \{(q_{1}, \varepsilon)\}$ … stav se nezměnil, ze zásobníku se přečetlo A – bylo odebráno
vrchol zásobníku běžného PDA se píše vlevo

Výpočet zásobníkového automatu

Definice 3.37. Konfigurace, krok výpočtu ²⁾

Nechť $M = (Q, \Sigma, \Gamma, \delta, q_{0}, Z_{0}, F)$ je PDA.
Konfigurací nazveme libovolný prvek $(p, w, \alpha) \in Q \times \Sigma^{*} \times \Gamma^{*}$ .
Na množině všech konfigurací automatu M definujeme binární relaci krok výpočtu $|\frac{\ \ \ }{\ M \ }$ takto:
$(p, aw, Z \alpha) |\frac{\ \ \ }{\ M \ }(q, w, \gamma \alpha) \Leftrightarrow^{def} \exists(q, \gamma) \in \delta (p, a, Z)$ pro $a \in \Sigma \cup \lbrace \varepsilon \rbrace$

Reflexivní a tranzitivní uzávěr relace $|\frac{\ \ \ }{\ M \ }$ značíme $|\frac{\ * \ }{\ M \ }$ .
Je-li M zřejmý z kontextu, píšeme pouze $|\frac{\ \ \ }{\ \ \ }$ resp. $|\frac{\ * \ }{\ \ \ }$ .

Akceptující výpočet PDA

Definice 3.37. (pokračování) - akceptování ³⁾

Jazyk akceptovaný PDA M koncovým stavem definujeme jako
$L(M) = \lbrace w \in \Sigma^{*} | (q_{0}, w, Z_{0}) |\frac{\ * \ }{\ \ \ } (q_{f}, \varepsilon, \alpha)$ , kde $q_{f} \in F, \alpha \in \Gamma^{*} \rbrace$

a jazyk akceptovaný PDA M prázdným zásobníkem definujeme
$L_{e}(M) = \lbrace w \in \Sigma^{*} | (q_{0}, w, Z_{0}) |\frac{\ * \ }{\ \ \ } (q, \varepsilon, \varepsilon)$ , kde $q \in Q \rbrace$ .

Takto definovaný PDA je nedeterministický – akceptuje slovo, jestliže existuje alespoň jeden výpočet, který vede z počáteční konfigurace do akceptující. V případě možnosti automat „hádá správně“.

Grafická reprezentace konfigurací

Zpravidla nekonečné
Vnitřní konfigurace (= částečná konfigurace) = aktuální stav a celý obsah zásobníku (vrchol se píše vlevo)

Příklad: PDA $A = (\{q, r\}, \{a, b, c\}, \{Z, A\}, \delta, q, Z, \{r\})$ - akceptuje koncovým stavem
PDA $A'= (\{q, r\}, \{a, b, c\}, \{Z, A\}, \delta, q, Z, \emptyset)$ - akceptuje prázdným zásobníkem

Přechodovou funkci mají oba automaty stejnou:
$\delta(q, a, Z) = \{(q, AZ)\}$ $\delta(q, a, A) = \{(q, AA)\}$ $\delta(q, c, Z) = \{(r, Z)\}$ $\delta(q, c, A) = \{(r, A)\}$ $\delta(r, b, Z) = \{(r, \epsilon)\}$ $\delta(r, b, A) = \{(r, \epsilon)\}$

Grafické znázornění obou automatů, žlutě vybarvené jsou konfigurace, ve kterých akceptuje automat A, v tlustě orámované konfiguraci akceptuje automat A'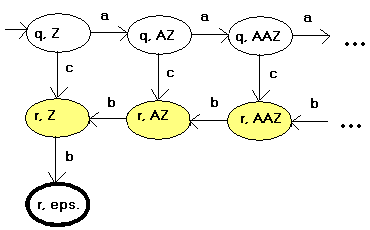

Ekvivalence dvou způsobů akceptování

Pro každý jazyk L platí:

Věta 3.39, ⁴⁾

$L = L(N)$ pro nějaký PDA N $\Leftrightarrow L = L_{e}(M)$ pro nějaký PDA M.

PDA N akceptuje koncovým stavem, PDA M prázdným zásobníkem

koncový stav => prázdná paměť

Intuice: K danému N zkonstruujeme M simulující jeho činnost.
Vejde-li N do koncového stavu, M se nedeterministicky rozhodne
• pokračovat v simulaci automatu N nebo
• přejít do nově přidaného stavu $q_{\varepsilon}$ , v němž vyprázdní zásobník.
Komplikace: Automat N by vyprázdnil zásobník, aniž by došel do koncového stavu – akceptoval by i nežádoucí vstup.
Řešení: Před zahájením simulace bude u M na dně zásovníku nový symbol, který nedovolíme odstranit jinde, než ve stavu $q_{\varepsilon}$ .

prázdná paměť => koncový stav

K danému M zkonstruujeme N simulující jeho činnost.
• N si před simulací přidá na dno zásobníku nový symbol.
• Je-li N schopen číst tento symbol (tj. zásobník automatu M je prázdný), potom N přejde do nově přidaného stavu $q_{f}$ , který je koncovým stavem.

důkaz viz skripta ⁵⁾, konstrukce viz slidy ⁶⁾

Rozšířený zásobníkový automat

Definice 3.44., Rozšířený PDA ⁷⁾

- sedmice $R = (Q, \Sigma, \Gamma, \delta, q_{0}, Z_{0}, F)$ , kde
• všechny symboly až na $\delta$ mají stejný význam jako v definici PDA,
• $\delta$ je zobrazením
z konečné podmnožiny množiny $Q \times (\Sigma \cup \lbrace \varepsilon \rbrace)\times\Gamma^{*}$ ,
do konečných podmnožin množiny $Q \times \Gamma^{*}$ .

Pojmy konfigurace a akceptovaný jazyk (koncovým stavem, prázdným zásobníkem) zůstávají beze změny. Krok výpočtu $|\frac{\ \ \ }{\ R \ }$ definujeme takto:
$(p, aw, \gamma_{1} \alpha) |\frac{\ \ \ }{\ R \ } (q, w, \gamma_{2} \alpha) \Leftrightarrow^{def} \exists(q, \gamma_{2}) \in \delta (p, a, \gamma_{1})$ pro $a \in \Sigma \cup \lbrace \varepsilon \rbrace$

Ekvivalence rozšířených PDA a PDA

Lemma 3.45. ⁸⁾

Ke každému rozšířenému PDA existuje ekvivalentní (obyčejný) PDA.

(Důkaz: skripta Formální jazyky a automaty I, str. 82)

Zásobníkové automaty a bezkontextové jazyky

Problém syntaktické analýzy pro bezkontextové gramatiky: pro danou bezkontextovou gramatiku G a slovo w rozhodnout, zda $w \in L(G)$ .

Ekvivalence bezkontextových gramatik a zásobníkových automatů

Věta 3.51 ⁹⁾

Ke každému PDA M lze sestrojit CFG G takovou, že $L_{e}(M) = L(G)$ .

Věta 3.47 ¹⁰⁾

Ke každé CFG G lze sestrojit PDA M takový, že $L(G) = L_{e}(M)$ .

Důsledek 3.52 ¹¹⁾

Třída jazyků rozpoznávaných zásobníkovými automaty je právě třída bezkontextových jazyků.

Konstrukce PDA řeší problém syntaktické analýzy. (platí pro dané G a w: $w \in L(G)?$ )
$w \in L(G) \Leftrightarrow$ v G existuje derivační strom s výsledkem w.

Nedeterministická syntaktická analýza shora dolů

Budování derivačního stromu simuluje levé derivace, tj. vždy rozvíjíme nejlevější neterminál.

Důsledek 3.47 ¹²⁾

Ke každé CFG G lze sestrojit PDA M takový, že $L(G) = L_{e}(M)$ .

Důkaz. K dané gramatice G konstruujeme PDA M, který simuluje levé derivace v G (rozvíjíme nejlevější neterminál).

V levé derivaci je v jednom kroku odvození nahrazen (nejlevější) neterminál A pravou stranou $X_{1} ...X_{n}$ nějakého A-pravidla.
V M této situaci odpovídá náhrada A na vrcholu zásobníku řetězem $X_{1} ...X_{n}$ .

$M = (\lbrace q \rbrace, \Sigma,N \cup \Sigma, \delta, q, S, \emptyset)$ , kde $\delta$ je definována:

$\delta(q, \varepsilon, A)$ obsahuje $(q, \alpha)$ právě když $A \rightarrow \alpha \in P$
$\delta(q, a, a) = \lbrace(q, \varepsilon)\rbrace$ pro všechna $a \in \Sigma$

korektnost + důkaz viz skripta ¹³⁾

Nedeterministická syntaktická analýza zdola nahoru

Lemma 3.55 ¹⁴⁾

Nechť G je libovolná CFG, pak lze zkonstruovat rozšířený PDA R takový, že L(G) = L(R).

Důkaz. Vrchol zásobníku píšeme vpravo. Konstruujeme rozšířený PDA R, který simuluje pravou derivaci v G v obráceném pořadí.
PDA R má kroky dvojího typu:

může kdykoli číst do zásobníku vstupní symbol,
(redukce) je-li na vrcholu zásobníku řetěz tvořící pravou stranu nějakého pravidla v G, může ho nahradit odpovídajícím levostranným neterminálem (a ze vstupu nic nečte).

Nechť $G = (N, \Sigma, P, S)$ .
Položme $R = (\lbrace q, r \rbrace, \Sigma, N \cup \Sigma \cup \lbrace \bot \rbrace, \delta, q, \bot, \lbrace r \rbrace )$ , kde $\bot$ je nově přidaný symbol a kde $\delta$ je definována takto:

$\delta(q, a, \varepsilon) = \lbrace(q, a)\rbrace$ pro všechna $a \in \Sigma$ …načítání vstupu na zásobník,
je-li $A \rightarrow \alpha$ , pak $\delta(q, \varepsilon, \alpha)$ obsahuje (q, A) …redukce,
$\delta(q, \varepsilon, \bot S) = \lbrace(r, \varepsilon)\rbrace$ …akceptování.

korektnost viz slajdy ¹⁵⁾

Příklad:

Zadání:
G = ({S, A, B}, {a, b}, P, S)
P =
{S → $\varepsilon$ | abSA
A → AaB | aB | a,
B → aSS | bA | $\varepsilon$ }
Derivační strom pro slovo w = abababaa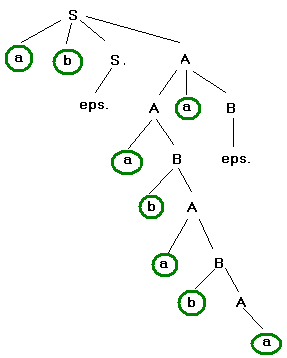
Automat, který provádí syntaktickou analýzu shora dolů: A = ({q}, {a,b}, {S, A, B, a, b}, $\delta$ , q, S, $\emptyset$ )
2 typy přechodových fcí:

levou stranu pravidel z gram. dáváme na zásobník levé strany přechodové fce PDA, pravou stranu pravidel z gram. na zásobník pravé strany

$\delta$ (q, $\varepsilon$ , S) = {(q, $\varepsilon$ ), (q, abSA)}
$\delta$ (q, $\varepsilon$ , A) = {(q, AaB), (q, aB), (q, a)}
$\delta$ (q, $\varepsilon$ , B) = { (q, aSS), (q, bA), (q, $\varepsilon$ )}

„mazací“ přechodové fce

$\delta$ (q, a, a) = {(q, $\varepsilon$ )}
$\delta$ (q, b, b) = {(q, $\varepsilon$ )}

Akceptující výpočet nad slovem abababaa:

(intuice: postupuju podle derivačního stromu, sleduju jeho rozvíjení odshora a čtu ho zleva)
vrchol zásobníku je vlevo $(q, abababaa, S) |\frac{\ \ \ }{\ \ \ } (q, abababaa, abSA) |\frac{\ \ \ }{\ \ \ } (q, bababaa, bSA) |\frac{\ \ \ }{\ \ \ }$
$(q, ababaa, SA) |\frac{\ \ \ }{\ \ \ } (q, ababaa, A) |\frac{\ \ \ }{\ \ \ } (q, ababaa, AaB) |\frac{\ \ \ }{\ \ \ }$
$(q, ababaa, aBaB) |\frac{\ \ \ }{\ \ \ } (q, babaa, BaB) |\frac{\ \ \ }{\ \ \ } (q, babaa, bAaB) |\frac{\ \ \ }{\ \ \ }$
$(q, abaa, AaB) |\frac{\ \ \ }{\ \ \ } (q, abaa, aBaB) |\frac{\ \ \ }{\ \ \ } (q, baa, BaB) |\frac{\ \ \ }{\ \ \ }$
$(q, baa, bAaB) |\frac{\ \ \ }{\ \ \ } (q, aa, AaB) |\frac{\ \ \ }{\ \ \ } (q, aa, aaB) |\frac{\ \ \ }{\ \ \ }$
$(q, a, aB) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, B) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, \varepsilon)$ … celé slovo se přečetlo a zásobník se vyprázdnil $\rightarrow$ automat slovo akceptuje

Automat pro syntaktickou analýzu zdola nahoru: $A_{2} = (\{q, r\}, \{ a,b\} , \{S, A, B, a, b, \bot\}, \delta, q, \bot, \{ r\})$ 3 typy přechodových funkcí:

terminály z gramatiky se předávají na zásobník

$\delta$ (q, a, $\varepsilon$ ) = {(q, a)}
$\delta$ (q, b, $\varepsilon$ ) = {(q, b)}

pravou stranu pravidel z gram. dáváme na zásobník levé strany přechodové fce PDA, levou stranu pravidel z gram. na zásobník pravé strany

$\delta$ (q, $\varepsilon$ , abSA) = {(q, S)}
$\delta$ (q, $\varepsilon$ , $\varepsilon$ ) = {(q, S), (q, B)} ! ! ! Nesmí být rozděleno na: $\delta$ (q, $\varepsilon$ , $\varepsilon$ ) = {(q, S)} a $\delta$ (q, $\varepsilon$ , $\varepsilon$ ) = {(q, B)}, nebyla by to pak funkce.
$\delta$ (q, $\varepsilon$ , AaB) = $\delta$ (q, $\varepsilon$ , aB) = $\delta$ (q, $\varepsilon$ , a) = {(q, A)}
$\delta$ (q, $\varepsilon$ , aSS) = $\delta$ (q, $\varepsilon$ , bA) = {(q, B)}

přechod do koncového stavu

$\delta$ (q, $\varepsilon$ , $\bot$ S) = {(r, $\varepsilon$ )}

Akceptující výpočet nad slovem abababaa:

(Intuice: čtu derivační strom zleva – jako když teče voda (= používám první skupinu pravidel), pokud by voda musela téct do kopce, použiju pravidlo z druhé skupiny)
vrchol zásobníku je vpravo $(q, abababaa, \bot) |\frac{\ \ \ }{\ \ \ } (q, bababaa, \bot a) |\frac{\ \ \ }{\ \ \ } (q, ababaa, \bot ab) |\frac{\ \ \ }{\ \ \ }$
$(q, ababaa, \bot abS) |\frac{\ \ \ }{\ \ \ } (q, babaa, \bot abSa) |\frac{\ \ \ }{\ \ \ } (q, abaa, \bot abSab) |\frac{\ \ \ }{\ \ \ }$
$(q, baa, \bot abSaba) |\frac{\ \ \ }{\ \ \ } (q, aa, \bot abSabab) |\frac{\ \ \ }{\ \ \ } (q, a, \bot abSababa) |\frac{\ \ \ }{\ \ \ }$
$(q, a, \bot abSababA) |\frac{\ \ \ }{\ \ \ } (q, a, \bot abSabaB) |\frac{\ \ \ }{\ \ \ } (q, a, \bot abSabA) |\frac{\ \ \ }{\ \ \ }$
$(q, a, \bot abSaB) |\frac{\ \ \ }{\ \ \ } (q, a, \bot abSA) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, \bot abSAa) |\frac{\ \ \ }{\ \ \ }$
$(q, \varepsilon, \bot abSAaB) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, \bot abSA) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, \bot S) |\frac{\ \ \ }{\ \ \ } (r, \varepsilon, \varepsilon)$ … automat přečetl celé slovo a přešel do koncového stavu r, slovo akceptuje.

U nedeterministické analýzy automat slovo neakceptuje, pokud žádný z možných výpočtů není akceptující.

Efektivnost syntaktické analýzy

Nederministický PDA ⇒ nedeterministický algoritmus ⇒ exponenciální deterministický algoritmus

Řešení: • deterministický algoritmus složitosti $O(n^{3})$ , kde n = |w| (algoritmus Cocke – Kasami – Younger)
• deterministické zásobníkové automaty a deterministické bezkontextové jazyky
• lineární algoritmy pro speciální třídy deterministických bezkontextových jazyků

C - Y - K algoritmus (Cocke - Younger - Kasami)

Problém: Lze v dané gramatice v CNF vygenerovat dané slovo w?
Řešení: Pro každé podslovo u slova w spočítáme množinu $T_{u}$ všech neterminálů, z kterých lze odvodit u.
* u = a
* u = ab
* u = abc
$T_{i, j} = \{ X| X \Rightarrow^{*} w_{i}w_{i+1}...w_{i+j}w_{i+j-1}\}$

Kubická složitost vzhledem k délce vstupního slova (velikost tabulky: $\frac{n^{2}}{2}$ , na vyplnění políčka je zapotřebí až n kroků.
Pracuje pouze s gramatikou v CNF (Chomského normální formě)

Algoritmus:

Algoritmus C - Y - K

Vstup: gramatika $G = (N, \Sigma, P, S)$ v CNF, slovo $w = w_{1}...w_{n}$ Poznámka: $T_{i,j} = {X | X \rightarrow^{*} w_{i}...w_{i+j-1}}$ for i:=1 to n do
$T_{i,1} := \bot$ for každé pravidlo $A \rightarrow a \in P$ do
if $a = w_{i}$ then $T_{i,1} := T_{i,1} \cup \lbrace A \rbrace$ fi
od od
for j:=2 to n do
for i:=1 to n-j+1 do
$T_{i,j}:= \bot$ for k:=1 to j-1 do
for každé pravidlo $A \rightarrow BC \in P$ do
if $B \in T_{i, k} \wedge C \in T_{i+k, j-k}$ then $T_{i, j}:= T_{i, j} \cup$ {A} fi

od od od od

Příklad

Je dána bezkontextová gramatika G = ({S,A,B,C}, {a, b, c, d}, P, S) v CNF, kde
P = { S → AA | BC | a | b,
A → BA | BB | a | c,
B → AB | CA | b,
C → BC | CC | SC | d }
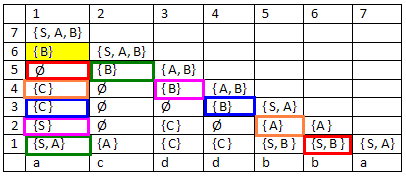
Syntaktická analýza slova $acddbba$ pomocí C-K-Y algoritmu:

Vidíme, že $S \in T_{1,7} = {S,B,A}$ , tedy $acddbba \in L(G)$ .

Intuitivní návod na vyplňování tabulky:

na nultý řádek napíšeme slovo, které chceme testovat (co sloupeček, to 1 terminál)
obsah každého políčka v 1. řádku tvoří množina neterminálů, ze kterých se vygenerují terminály v příslušném sloupečku nultého řádku
další řádky se vyplňují stylem, který je naznačený u žlutého políčka: do množiny v políčku se zapíší všechny neterminály, které generují všechny dvojice neterminálů z příslušných dvojic políček - každá používaná dvojice políček je orámovaná stejnou barvou.

Pro žluté políčko vezmeme jednu z dvojic políček - např. tu orámovanou zeleně. Vzniklé dvojice neterminálů jsou SB a AB. SB není generována žádným neterminálem, tedy do žlutého políčka nepřipisuju nic. AB je generovaná B, proto B zapíšu do žlutého políčka. Stejně postupuju i u ostatních dvojic políček.

Možnost, jak vybírat správné dvojice políček: začínám políčkem, které je nejníž v příslušném sloupečku a políčkem, který je nejblíž v úhlopříčce směrem doprava (pro žluté políčko to jsou zelené rámečky) a dál postupuju (podle krásně jednoduchého návodu Vaška Brožka:), tak že lezu nahoru po žebříku (ve sloupečku) a sestupuju po schodech (v úhlopříčce).

Předměty

IB102 Automaty a gramatiky IB005 Formální jazyky a automaty I

Literatura

Skripta Formální jazyky a automaty I
Slajdy k přednáškám IB102 na stránkách Jana Strejčka

Vypracoval

Didl - Dita Dlabolová
Stav: 100%, z mé strany hotovo a zkontrolováno.

Je potřeba ještě zapracovat poznámky od Jitky Pospíšilové.

¹⁾

skripta Automaty a formální jazyky I, str. 77

²⁾ , ³⁾ , ⁴⁾

skripta Automaty a formální jazyky I, str. 78

⁵⁾

skripta Automaty a formální jazyky I, str. 78

⁶⁾

Web IB102 - slajdy10, str. 5 a 8

⁷⁾ , ⁸⁾

skripta Formální jazyky a automaty I, str. 82

⁹⁾

skripta Formální jazyky a automaty I, str. 86

¹⁰⁾ , ¹²⁾

skripta Formální jazyky a automaty I, str. 83

¹¹⁾

skripta Formální jazyky a automaty I, str. 89

¹³⁾

str. 84 skripta Formální jazyky a automaty I, slajdy11 - str. 12

¹⁴⁾

skripta Formální jazyky a automaty I, str. 90

¹⁵⁾

slajdy11, str. 17