Obsah
AP16, IN16 Třídění
Zadání
(základní algoritmy, algoritmy řazení haldou, slučováním, rozdělováním)
Pre IN otázka pokračuje Grafovými algoritmami.
Algoritmy vnitřního třídění
Vnitřní třídění je takové třídění, kdy předem známe tříděné prvky a máme k dispozici dostatek volné paměti, abychom je uvnitř této paměti mohli setřídit. Opakem je pak třídění vnější, kdy jednotlivé prvky předem neznáme a musíme je ze vstupu postupně načítat v pořadí, v jakém přicházejí. Toto třídění se provádí typicky v situacích, kdy máme operační paměti málo a nejsme schopni v ní všechny prvky uložit. Ve vnějším třídění proto využijeme vnější paměti - pracujeme s jednotlivými soubory na disku. Teoreticky tak můžeme setřídit daleko větší množství dat, operace s vnější pamětí jsou však také podstatně pomalejší. Práce se soubory rychlé algoritmy podstatně degraduje.
Úlohu vnitřního třídění založeného na porovnávání dvou prvků lze vždy řešit algoritmem se složitostí ve třídě O(n log n) (takové výborné složitosti dosahuje Heap Sort). Některé jiné algoritmy (Quick Sort, nejrychlejší algoritmus v průměrném případě) mohou v ideálním případě dosahovat i lineární složitosti (O(n)), jiné zase často dosahují složitostí vyšších (O(n2)).
SelectSort
ShellSort
RadixSort
MaxSort
BubbleSort
ShakeSort
InsertionSort
HeapSort
QuickSort
MergeSort
Poslední dvě zmíněné se většinou implementují rekurzivně. Není to ale podmínkou.
Selection Sort (SelectSort)
Uspořádávání přímým výběrem
Přímý výběr je přímočarý a jednoduchý algoritmus, který je vhodné použít u krátkých polí. Algoritmus projde celé pole a najde nejmenší prvek, který prohodí s prvním prvkem pole. Takto získané pole má nejmenší prvek na začátku. Algoritmus pokračuje hledáním nejmenšího čísla, které umístí na pozici o jednu větší, než při předchozím průchodu.
Složitost algoritmu Select Sort je O(n2). Speciální variantou je pak Bidirectional Selection Sort (známý i jako Shaker Sort; více informací o jménech najdete u Bidirectional Bubble Sortu), který během průchodu hledá jak nejmenší, tak největší hodnotu, čímž redukuje počet průchodů na polovinu.
3 5 2 1 4 10 8 6 9 7
1 5 2 3 4 10 8 6 9 7
1 2 5 3 4 10 8 6 9 7
1 2 3 5 4 10 8 6 9 7
1 2 3 4 5 10 8 6 9 7
1 2 3 4 5 10 8 6 9 7
1 2 3 4 5 6 8 10 9 7
1 2 3 4 5 6 7 10 9 8
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
Neaktivní čísla
První ze zaměňovaných čísel
Druhé ze zaměňovaných čísel
Max Sort
Max Sort je algoritmus téměř totožný s Select Sortem, jen probíhá obráceně (od největšího k nejmenšímu).
Bubble Sort
Bublinkové třídění
Tento algoritmus je velmi pomalý v neuspořádaných polích, ale zato velmi efektivní v polích částečně uspořádaných. Postupně se systematicky porovnávají dvojice sousedních prvků a vyměňují se spolu vždy, když menší číslo následuje po větším. Po prvním průchodu FOR cyklem je zajištěno, že největší číslo je na konci pole. Druhý průchod už můžeme provádět jen ve zbytku pole. Po ukončení druhého průchodu jsou největší dvě čísla správně umístěna. Celý postup opakujeme až do uspořádání celého pole.
Průměrná i nejhorší asymptotická složitost je O(n2).
3 5 2 1 4 10 8 6 9 7
3 2 1 4 5 8 6 9 7 10
2 1 3 4 5 6 8 7 9 10
1 2 3 4 5 6 7 8 9 10
Zaměňovaná čísla
Čísla jdoucí na konec
Bidirectional Bubble Sort
Třídění přetřásáním
Tento algoritmus vychází z bublinkového třídění, které zlepšuje tak, že probublávají střídavě malá čísla na levý okraj a velká čísla na pravý okraj. Ve učebních materiálech se setkáte s názvem Shaker Sort, který ale může znamenat i speciální variantu selection sortu.
Insertion Sort
Třídění vkládáním
Třídění vkládáním je rychlejší než Select Sort, ale pomalé vzhledem ke Quick Sortu (složitost je stále O(n2)). Třídící metoda spočívá ve vkládání čísla před nejmenší větší číslo. Vkládání probíhá do neustále se zvětšující části pole (seřazené).
3 5 2 1 4 10 8 6 9 7
2 3 5 1 4 10 8 6 9 7
1 2 3 5 4 10 8 6 9 7
1 2 3 4 5 10 8 6 9 7
1 2 3 4 5 10 8 6 9 7
1 2 3 4 5 8 10 6 9 7
1 2 3 4 5 6 8 10 9 7
1 2 3 4 5 6 8 9 10 7
1 2 3 4 5 6 7 8 9 10
Neaktivní čísla
Aktivní čísla (se kterými se pracuje)
Čísla, která se přesunula
Pozn. Prvky se vybírají jen z nesetříděné části pole.
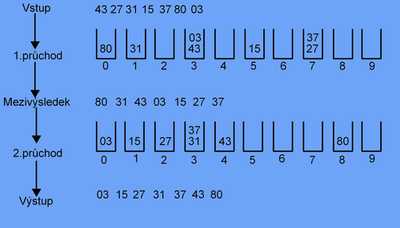
Radix Sort
Tato metoda třídí posloupnost k-místných čísel délky n a pracuje na principu přihrádkového řazení.
Pomocí datové struktury fronta se zde zavádí deset přihrádek – jedna pro každou číslici z intervalu 0 až 9. Vlastní třídění probíhá takto: v prvním průchodu vstupní posloupností čísla zařazujeme do vzniklých přihrádek podle jejich poslední číslice (jednotky), poté čísla spojíme z přihrádek do nové posloupnosti; v dalším průchodu čísla z této nové posloupnosti zařazujeme do vzniklých přihrádek podle jejich předposlední číslice (desítky), poté čísla spojíme do další nové posloupnosti; takto provádíme rozdělování a spojování po jednotlivých řádech číslic až do řádu k.
Důležitá poznámka – čísla z přihrádek vybíráme do nové posloupnosti v takovém pořadí, v jakém jsme je do přihrádek vložili – proto využíváme datovou strukturu fronta.1)
Slovensky
pripravíme k pomocných kôpok, do ktorých budeme prehadzovať hodnoty zo vstupnej postupnosti
k – počet rôznych hodnôt, ktoré môžu nadobúdať jednotlivé cifry (napr. pre čísla 10, pre znaky 26 a pod.)
v prvom prechode postupne prehadzujeme všetky hodnoty do príslušnej kôpky podľa poslednej cifry
potom všetky kôpky spojíme – zoradíme opäť do jednej postupnosti
v druhom prechode prehadzujeme hodnoty do kôpok podľa predposlednej cifry
opäť ich potom spojíme do jednej postupnosti (v pořadí v jakém byly vloženy - fronta)
toto postupne opakujeme pre všetky cifry – na záver je celá postupnosť utriedená vzostupne
takto sa dobre triedia spájané zoznamy
pri práci s poliami si tento algoritmus vyžaduje veľa pomocných polí.
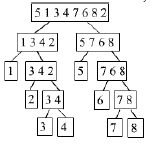
Merge Sort
Třídění slučováním
Tento algoritmus rozdělí pole na dvě přibližně stejně velké části. Poté s každou z těchto částí učiní totéž – rozdělí na dvě, dokud nedostaneme jednoprvkové úseky. Jednopoložkové úseky jsou vždy utříděné, takže teď bereme utříděné úseky a slučujeme tak, aby byly zase utříděné(2 úseky se musí znovu setřídit, ne jen spojit). Končíme, až když uspořádáme celé pole. Složitost Merge Sortu je O(n log n).
| 3 | 5 | 2 | 1 | 4 | 10 | 8 | 6 | |||||||
| 3 | – | 5 | – | 2 | – | 1 | – | 4 | – | 10 | – | 8 | – | 6 |
| 3 | 5 | – | 1 | 2 | – | 4 | 10 | – | 6 | 8 | ||||
| 1 | 2 | 3 | 5 | – | 4 | 6 | 8 | 10 | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
MergeSort ve funkcionálním zápisu
mergeSort :: [Int] -> [Int]
mergeSort [] = []
mergeSort [x] = [x]
mergeSort s = merge (mergeSort u) (mergeSort v)
where (u,v) = splitAt (n ‘div‘ 2) s
n = length s
merge s [] = s
merge [] t = t
merge (x:u) (y:v) = if x≤y then x: merge u (y:v)
else y: merge (x:u) v
Výhody a nevýhody: Velkou nevýhodou oproti algoritmům stejné rychlostní třídy (např. Heapsort) je, že Mergesort pro svou práci potřebuje navíc pole o velikosti N. Existuje sice i modifikace Mergesortu, která toto pole nepotřebuje, ale její implementace je velmi složitá a díky vysokému overheadu i pomalá. Kromě toho se Mergesort také ukazuje být pomalejší než Quicksort nebo Heapsort. Na druhou stranu je Mergesort stabilní řadící algoritmus, lépe se paralelizuje a má vyšší výkon na sekvenčních médiích s nižší přístupovou dobou. V mnoha implementacích programovacích jazyků je Mergesort implicitním řadícím algoritmem (v Perlu 5.8, v Javě nebo v GNU C Library). 2)
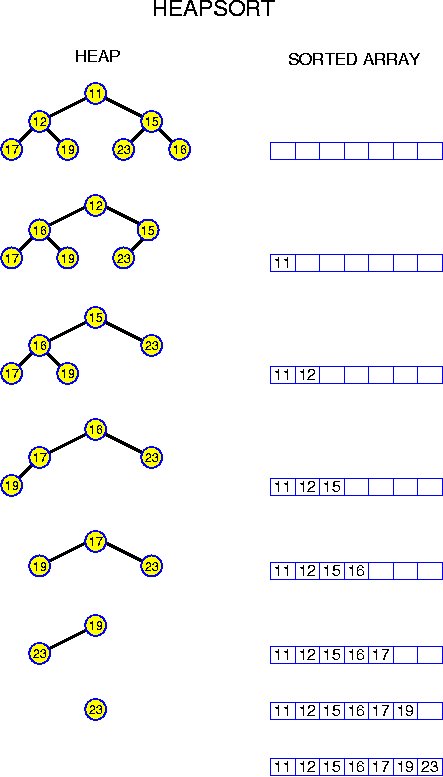
Heap Sort
Třídění pomocí „haldy“
V Heap Sortu se nejdříve vytvoří (binární) haldy. Binární halda je binární strom, pro který platí:
- Délky všech větví se liší nejvýše o 1: mají délku k, případně k − 1. Číslu k pak říkáme hloubka haldy.
- Pokud nejhlubší úroveň haldy není kompletně zaplněna, uzly na této úrovni jsou zaplňovány zleva.
- Hodnoty uzlů na každé větvi jsou vzestupně (sestupně) uspořádány.
Jsou-li hodnoty uzlů na každé větvi seřazeny vzestupně (čím dále od kořene, tím větší hodnoty), je v kořenu haldy nejmenší prvek. Hovoříme pak o minimové haldě (min-heap).
Jsou-li hodnoty uzlů na každé větvi seřazeny sestupně (čím dále od kořene, tím menší hodnoty), je v kořenu haldy největší prvek. Hovoříme pak o maximové haldě (max-heap).3)
Věta: Neprázdná binární halda na n uzlech má hloubku .4)
Z výše uvedeného vyplývá, že každé patro haldy musí být kompletně zaplněno, pouze poslední patro nemusí mít plný počet prvků. Při přidání dalšího prvku se musí pole znovu „uhaldovat“ – prvek se přidá jako syn a pokud je menší (v případě min-heapu)/větší (v případě max-heapu) než otec, potom se s ním vymění. Pokud je i pak jeho otec menší/větší než přidaný prvek, opět se prohodí atd.
Věta: Algoritmus řazení haldou má složitost Θ(n log n). 5)
Práci s haldou je možné si interaktivně vyzkoušet.
Ve funkcionální implementaci algoritmu řazení haldou, kde se pracuje s explicitní haldou (datovou strukturou binární strom), použijeme minimovou haldu. Naopak v imperativní implementaci, kde se pracuje s implicitní haldou (reprezentovanou polem), je výhodnější použít maximovou haldu.6)
Quick Sort
Řazení rozdělováním
Jedná se o rekurzivní třídění
Quick Sort je znatelně nejrychlejší ze zde zmíněných algoritmů. Princip Quick Sortu je velmi jednoduchý – pouze rozdělí čísla na menší a větší. Při opětovném zavolání se rozdělí menší zase na menší-menší a menší-větší a toto se provede i u větších (rozdělí se na větší-menší a větší-větší). Pří dalším zavolání se zase rozdělí každá část na menší a větší, až zbude v každé části pouze jedno číslo, nebo bude daná část uspořádaná.
3 5 2 1 4 10 8 6 9 7
3 4 2 1 5 10 8 6 9 7
3 4 2 1 / 5 10 8 6 9 7
3 1 2 / 4 / 5 7 6 / 8 9 10
1 / 3 2 / 4 / 5 6 / 7 8 9 10
1 / 2 / 3 / 4 / 5 6 / 7 / 8 9 10
Neaktivní čísla
Střed pole (pivot)
Prohozená čísla
1/2 část původního pole
Jiná definice
Příklad: Máme posloupnost 5 1 3 4 7 6 8 2. Z posloupnosti vybereme nějaké číslo (a právě výběr tohoto čísla působí na složitost). Následně posloupnost rozdělíme na dvě části. V první části budou všechna čísla menší než zvolené číslo, v druhé části pak čísla větší nebo rovná vybranému číslu.
QuickSort ve funkcionálním zápisu
quickSort :: [Int] -> [Int]
quickSort [] = []
quickSort (p:t) = quickSort lt ++ [p] ++ quickSort ge
where lt = [ x | x <- t, x < p ]
ge = [ x | x <- t, x ≥ p ]
Ukázka implementace některých algoritmů a jejich složitost
Bubble sort (bublinkové třídění)
procedure BubbleSort(var pole:TPole; N:word); var i,j, pom: integer; begin for j:=1 to N-1 do {probublavani provadime pro n-1 prvku} for i:=1 to N-1 do {postupne pro vsechny prvky pred poslednim} if pole[i]>pole[i+1] then {pokud je prvek mensi nez nasledujici} begin {prehod prvky => probublavani vetsiho prvku polem} pom:=pole[i+1]; {prvky snadno prohodime pomoci pomocne promenne pom} pole[i+1]:=pole[i]; pole[i]:=pom end end;
Algoritmus postupně „bere“ jednotlivé prvky pole (n − 1 prvků) a posouvá je dále doprava, dokud jsou větší než prvek před nimi.
Pro začátek se podíváme podrobněji na určení složitosti algoritmu: Složitost algoritmu je evidentně O(n2), algoritmus prochází pole o n prvcích ve dvou vnořených cyklech, každý cyklus sestává přibližně z n operací (přibližně n operací pro každých n prvků, tj. celkem n2), počet výměn prvků a přiřazovacích operací ve vnitřním cyklu se projeví jako multiplikativní konstanta, kterou lze ve výsledku zanedbat (jedná se jen o konstantní operace, které jsou samy o sobě nezávislé na velikosti vstupních dat). Lepší složitosti se dá dosáhnout drobnými vylepšeními algoritmu. Pro velká vstupní data není složitost O(n2) nejvhodnější, nejrychlejší třídící algoritmus v nejhorším případě – Heap Sort (třídění haldou) – dosahuje složitosti lineárně logaritmické. Přesto v jednoduchém případě můžeme tento algoritmus využít.
Vylepšený Bubble sort
procedure BubbleSort(var pole:TPole; N:word); var i,j, pom: integer; konec: boolean; begin for j:=1 to N-1 do begin {probublavani provadime pro n-1 prvku} konec:=true; {pred zacatkem vnitrniho cyklu nastavime konec na true} for i:=1 to N-1 do {postupne pro vsechny prvky pred poslednim} if pole[i]>pole[i+1] then {pokud je prvek mensi nez nasledujici} begin {prehod prvky => probublavani vetsiho prvku polem} pom:=pole[i+1]; pole[i+1]:=pole[i]; pole[i]:=pom; konec:=false {s prvkem se provedla vymena} end; if konec then Break {pokud nebyl ani jeden prvek v cyklu vymenen, tj. vsechny prvky byly uz na svem miste, ukoncime trideni (bylo by zbytecne setridene prvky dale prochazet} end end;
Složitost algoritmu v nejhorším případě zůstává stejná (O(n2)), pokud je však vstupní pole už relativně setříděné, často si ušetříme zbytečné automatické procházení tím, že si zaznamenáme průchod, v kterém byly už všechny prvky umístěné ve správném pořadí – konec třídění.
Třídění přímým výběrem minima
procedure PrimyVyber(var pole:TPole; N:word); var i,j, min, pom: integer; begin for i:=1 to N-1 do {na tyto pozice budeme vybirat minimum} begin min:=i; {nastaveni pozice minima} for j:=i+1 to N do {vyhledani mozneho minima v dalsich prvcich} if pole[j]<pole[min] then min:=j; if pole[min]<pole[i] then {pokud byl nalezen mensi prvek} begin {-> provedeni vymeny prvku} pom:=pole[i]; pole[i]:=pole[min]; pole[min]:=pom end end end;
Algoritmus postupně prochází pole a na dané místo hledá minimum ze zbývajících prvků. Ve for cyklu se prochází postupně (n − 1) + (n − 2) + (n − 3) + … + 1 prvků, tj. po sečtení , řádově je tedy složitost opět O(n2).
Třídění přímým vkládáním
procedure PrimeVkladani(var pole:TPole; N:word); {prvky postupne zarazujeme do leve casti pole - vytvarime setridene pole} var i,j, pom: integer; begin for i:=2 to N do {prochazime nesetridenou cast pole} begin pom:=pole[i]; {ulozime si zatrizovany prvek} for j:=i-1 downto 1 do {tento i-ty prvek zarazujeme do leve setridene casti pole} if pole[j]>pole[j+1] then begin {jestlize je prvek vlevo vetsi, prvky prehodime} pole[j+1]:=pole[j]; pole[j]:=pom end end end;
Algoritmus prvky z pravé části pole přímo zatřiďuje do levé části, kde se utváří seřazená posloupnost, postupně procházíme 1 + 2 + 3 + 4 + 5 + … + (n − 1) prvků jako v minulém případě, složitost je tedy také O(n2), jediný rozdíl tkví v tom, že tento způsob manipuluje při řazení přímo s jednotlivými prvky a ne jenom s jejich indexy.
Quick Sort (rekurzivní)
procedure QuickSort(var pole:TPole; Zac,Kon:integer); {procedura setridi v poli usek od indexu Zac do indexu Kon} var P: integer; {hodnota pro rozdeleni pole na useky - pivot} pom: integer; {pomocna promenna pro vymenu prvku} i,j: integer; {pracovni indexy pro vymezeni casti pole} begin i:=Zac; {na zacatku zabiraji mezni indexy cele pole} j:=Kon; P:=pole[(Zac+Kon) div 2]; {urcime si pivotni prvek - vezmeme prostredni prvek pole} {idealni pivot by byl median - prostredni z hodnot v poli} repeat {nalevo od pivota budeme radit mensi prvky, napravo vetsi prvky nez pivot} while pole[i]<P do inc(i); {posouv me levě index, dokud neni na prvku vetsim nez pivot} while pole[j]>P do dec(j); {posouvame pravy index, dokud neni na prvku mensim nez pivot} if i<j then {pokud se indexy neprekrizily a nejsou shodne} begin pom:=pole[i]; {vymenime nalezene prvky} pole[i]:=pole[j]; pole[j]:=pom; inc(i); dec(j); {a posuneme indexy na dalsi prvky} end else if i=j then {pokud se indexy sesly (ukazuji na pivota)} begin inc(i); {posunume je jeste dale, aby vymezovaly roztridene poloviny pole} dec(j); {a doslo k prekrizeni, coz vede k ukonceni cyklu} end until i>j; {opakujeme, dokud nejsou obeti casti pole roztrideny podle pivota} {Pole [Zac,Kon] je rozdeleno na 2 useky [Zac,j] a [i,Kon], ktere zpracujeme rekurzivne (opet touto procedurou)} if Zac<j then QuickSort(pole,Zac,j); {ma smysl tridit nejmene dva prvky} if i<Kon then QuickSort(pole,i,Kon); end;
Funkce algoritmu je dostatečně zřejmá z komentářů, takže stručně o co jde: Quick Sort vychází z rekurzivního přístupu – pokud máme třídit elementární pole o dvou prvcích, prvky jednoduše přehodíme na tu stranu, kam patří (porovnat je můžeme s pomyslnou hodnotou mezi nimi – pivotním prvkem). Pokud máme třídit pole větší, roztřídíme takto podle zvoleného pivota i dva velké úseky pole, které potom dále necháme třídit rekurzivně stejnou procedurou, až budou nakonec uspořádány všechny části pole. Tento algoritmus je typickým příkladem použití metody „rozděl a panuj“ (Divide & Impera), kdy programátor daný problém rozdělí na více jednoduchých elementárních problémů, které lze snadno vyřešit (třeba rekurzí). Pokud si vzpomenete na tento princip a vybavíte si postup, určitě pak budete schopni jednotlivé detaily algoritmu snadno doprogramovat.
Průměrná složitost Quick Sortu je O(n log n), přesněji O(n log2n), táto složitost nastává, pokud je vždy ideálně vybrán pivot jako prvek s prostřední hodnotou, nejhorší případ O(n2) nastává, pokud je pivot vždy nešikovně vybrán jako hodnota maximální nebo minimální. Výše uvedená procedura vybírá pivotní prvek jako střed pole, záleží ale na rozložení vstupních dat, každý z prvků pole je pro určitou kombinaci ideální, výběr se proto někdy provádí náhodně (pomocí generátoru náhodných čísel), což zaručuje, že při různém výběru pivotů nebude volba pro vstupní data vyloženě nevhodná a složitost se tak více přiblíží k očekávané složitosti O(n log n). V průměrném případě se v pravé a levé části pole zaměňuje vždy polovina prvků – pro jednotlivé zmenšující se úseky tedy ,
,
,
… – a vzhledem k tomu, že po záměně prvků se každé pole rozdvojuje na dvě poloviny (políčka si můžeme nakreslit do vyváženého binárního stromu), je složitost násobena dvojkovým logaritmem (zhruba zapisujeme jen logaritmus desítkový). Výsledná průměrná složitost je tedy intuitivně:
log n ( +
+
+
+ …) = n log n
Kam dál
Grafická ukázka řazení použitím algoritmů – http://www.cs.ubc.ca/~harrison/Java/sorting-demo.html applety mj animuje operace nad haldou Heap, Merge a Quick Sort -- pekne zpracovane
Literatura:
http://www.beranr.webzdarma.cz/algoritmy/trideni.html http://www.sweb.cz/HonzaRug/Delphi/alg.htm http://users.informatik.uni-halle.de
Vypracoval
Petr Kott
petr.kott@post.cz
Otázku si přečetl pan RNDr. Jan Bouda a rámcově prošel. Jeho podněty pro doplnění textu, opravy nesrovnalostí a odstranění matoucích či k otázce se nevztahujících textů byly do otázky zaneseny. Tato kontrola je jen rámcová, stále se může stát, že v otázce zůstala zapomenutá chybka či nesrovnalost, vyučující za toto nenese odpovědnost, berte tuto rámcovou kontrolu jako formu pomoci od vyučujících pro studenty.