Obsah

AP3, IN3 Uspořádání
Diskuze

AP3, IN3 Uspořádání

(relace uspořádání, uspořádané množiny a svazy, číselné obory)

Vypracovanie

Relace usporiadania

Usporiadanie a predusporiadanie

Relace $R \subseteq M \times M$ je usporiadanie práve vtedy, keď R je reflexívna, antisymetrická a tranzitívna.
Relace $R \subseteq M \times M$ je predusporiadanie (kvaziusporiadanie, polousporiadanie) práve vtedy, keď R je reflexívna a tranzitívna (a neplatí antisymetrie).

Usporiadané množiny

Usporiadaná množina

(Pred)usporiadaná množina je dvojica $(M,\sqsubseteq)$ , kde M je množina a $\sqsubseteq$ je (pred)usporiadanie na M.
Usporiadaná množina $(M,\sqsubseteq)$ sa nazýva lineárne usporiadaná (reťazec), ak $\forall a, b \in M:\ a \sqsubseteq b\ \vee \ b \sqsubseteq a$ (každé dva prvky sú zrovnateľné).

Príkladom lineárne usporiadaných množín sú N, Z, Q, R vzhľadom k usporiadaniu podľa veľkosti. Príkladom predusporiadanej množiny, ktorá nie je usporiadaná je (Z*,|), kde Z* je množina všetkých nenulových celých čísel a | je relace deliteľnosti (množina (N,|) usporiadaná je) ¹⁾.

Na usporiadaných množinách môžeme definovať ďalšie relace usporiadania:

usporiadanie po bodoch

Nech M je množina a $(A,\leq)$ usporiadaná množina. Nech $F = \{f|f:\ M \rightarrow A\}$ . Definujeme binárnu relaci $\sqsubseteq$ na F predpisom:
$f\ \sqsubseteq \ g \ \Leftrightarrow \ \forall x \in M:\ f(x) \leq g(x)$ Potom $(F,\sqsubseteq)$ je usporiadaná množina a usporiadanie $\sqsubseteq$ sa nazýva „po bodoch“.

usporiadanie po zložkách

Nech $(A,\leq)$ a $(B,\preceq)$ sú usporiadané množiny. Definujeme binárnu relaci $\sqsubseteq$ na $A \times B$ predpisom:
$(a,b)\ \sqsubseteq \ (a',b')\ \Leftrightarrow \ a \leq a'\ \wedge \ b \preceq b'$ Potom $(A \times B,\sqsubseteq)$ je usporiadaná množina a usporiadanie $\sqsubseteq$ sa nazýva „po zložkách“.

usporiadanie lexikografické

Nech $(A,\leq)$ a $(B,\preceq)$ sú usporiadané množiny. Definujeme binárnu relaci $\sqsubseteq$ na $A \times B$ predpisom:
$(a,b)\ \sqsubseteq \ (a',b')\ \Leftrightarrow \ (a \leq a'\ \wedge\ a \neq a')\ \vee \ (a = a'\ \wedge \ b \preceq b')$ Potom $(A \times B,\sqsubseteq)$ je usporiadaná množina a usporiadanie $\sqsubseteq$ sa nazýva „lexikografické“. Ak sú usporiadania $\leq$ a $\preceq$ lineárne, je aj usporiadanie $\sqsubseteq$ lineárne.

Nech $(A,\leq)$ je usporiadaná množina.
Najmenší prvok je prvok $x \in A$ taký, že $\forall y \in A:\ x \leq y$ .
Minimálny prvok je prvok $x \in A$ taký, že $\forall y \in A:\ y \leq x \Rightarrow x \leq y$ (x je minimálny práve vtedy, keď neexistuje žiadny prvok menší ako x).
Najväčší prvok je prvok $x \in A$ taký, že $\forall y \in A:\ y \leq x$ .
Maximálny prvok je prvok $x \in A$ taký, že $\forall y \in A:\ x \leq y \Rightarrow y \leq x$ (x je maximálny práve vtedy, keď neexistuje žiadny prvok väčší ako x).

Najmenší (najväčší) prvok, ak existuje, je jediný a zároveň minimálny (maximálny). Minimálnych (maximálnych) prvkov môže byť viac, potom ale neexistuje najmenší (najväčší) prvek.

Usporiadané množiny môžeme prehľadne zobraziť pomocou tzv. Hasseovských diagramov. Nech sú usporiadané množiny zadané nasledovne ²⁾: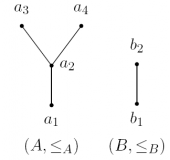
Prvok a₁ je minimálny a najmenší, prvky a₃, a₄ sú maximálne. Prvok b₁ je minimálny a najmenší, prvok b₂ maximálny a najväčší.
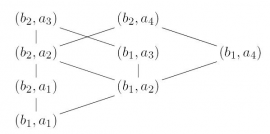
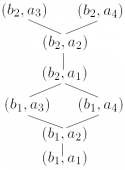
Pomocou Hasseovských diagramov môžeme znázorniť usporiadané množiny $(B \times A, \leq)$ , kde $\leq$ je usporiadanie po zložkách a $(B \times A, \preceq)$ , kde $\preceq$ je lexikografické usporiadanie:

Svazy

Svaz

Svaz je uspořádaná množina $(X,\preceq)$ , ve které existuje supremum i infimum pro libovolnou dvojici prvků. Ve svazu můžeme na supremum a infimum pohlížet jako na binární operace (protože je zaručeno, že jejich hodnoty jsou definovány pro každou dvojici). Supremum prvků x, y zde značíme $x \vee y$ , infimum jako $x \wedge y$ .
Definice svazu ze skript:³⁾.

Nech $(M,\leq)$ je usporiadaná množina.
Prvok $x \in M$ je horná závora množiny $A \subseteq M \Leftrightarrow \forall y\in A:\ y \leq x$ .
Prvok $x \in M$ je suprémum množiny $A \subseteq M$ (supA) $\Leftrightarrow$ x je najmenšia horná závora množiny A (t.j. pre ľubovoľnú hornú závoru y množiny A platí $x \leq y$ ).
Prvok $x \in M$ je dolná závora množiny $A \subseteq M \Leftrightarrow \forall y\in A:\ x \leq y$ .
Prvok $x \in M$ je infimum množiny $A \subseteq M$ (infA) $\Leftrightarrow$ x je najväčšia dolná závora množiny A (t.j. pre ľubovoľnú dolnú závoru y množiny A platí $y \leq x$ ).
Špeciálne prípady:⁴⁾.
Přehledné vysvětlení i s příklady:⁵⁾.
$sup\emptyset$ je najmenší prvok usporiadanej množiny M a $inf\emptyset$ je najväčší prvok M (ak existujú).
V usporiadanej množine $(P(M),\subseteq)$ , kde P(M) je potenčná množina množiny M a X je neprázdna podmnožina P(M) platí:
$supX = \bigcup X$ $infX = \bigcap X$

Veta 1 (Faktická správnost věty 1 je zpochybněna, viz diskusi)

Nech A je usporiadaná množina, potom nasledujúce výroky sú ekvivalentné.

ľuboboľná podmnožina množiny A má infimum
ľuboboľná podmnožina množiny A má suprémum

Dôkaz predchádzajúcej vety môžete nájsť v skriptách ⁶⁾.

Svaz a úplný svaz

Usporiadaná množina A sa nazýva svaz, ak jej ľubovoľná dvojprvková podmnožina má suprémum a infimum.
Nechť (A,∧,∨) je svaz a B je neprázdná podmnožina A. Pak B se nazývá podsvazem svazu A, platí-li, že B je uzavřená vzhledem ke svazovým operacím „∧“ a „∨“, tedy pro všechny a,b z B: a ∧ b náleží B, a ∨ b náleží B.
Usporiadaná množina A sa nazýva úplný svaz, ak jej ľubovoľná podmnožina má suprémum a infimum.

Z predchádzajúcich definícií vyplývajú nasledovné dôsledky:

Ak je $(A,\leq)$ svaz, potom tiež každá neprázdna konečná podmnožina v A má suprémum a infimum. Ak A je konečná (a neprázdna), pojmy svaz a úplný svaz splývajú.
Každý úplný svaz je tiež svaz.
Každý úplný svaz $(A,\leq)$ má najmenší a najväčší prvok, ktorým je $infA$ a $supA$ .

Príklady svazov a úplných svazov:

Každá lineárne usporiadaná množina je svaz, teda aj $(N,\leq)$ , $(Z,\leq)$ , $(Q,\leq)$ , $(R,\leq)$ sú svazy (žiaden z nich nie je úplný svaz (neexistuje supN, supZ), pokud se na uspořádání na daných množinách díváme tak, jak je obvyklé, ovšem tyto množiny lze přeuspořádat tak, aby již byly úplným svazem).
Usporiadaná množina $(N,|)$ je svaz – každá dvojprvková množina $\{a,b\}$ má suprémum (najmenší spoločný násobok a,b) a infimum (najväčší spoločný deliteľ a,b).

Uspořádaná množina $(N_{0},|)$ je úplný svaz. (Záleží tedy i na tom, jak si zadefinujeme relaci |. Například nechť $a,b \in N_{0}$ , $a | b \Leftrightarrow \exists x \in Z^{*}.\ a \cdot x = b\$ .)

Usporiadaná množina $(P(A),\subseteq)$ je úplný svaz, nájdenie supréma a infima ľubovoľnej podmnožiny je popísané vyššie.

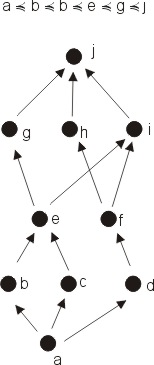
Krásně nakreslený příklad svazu + suprema a infima pro jeho podmnožiny 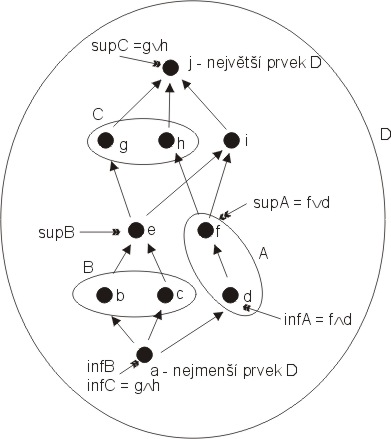zdroj⁷⁾

Číselné obory

Prirodzené čísla

Medzi prirodzené čísla N patria čísla 1, 2, 3, 4, 5,…, do N₀ patrí aj 0. Prirodzené čísla konštruujeme pomocou množín:
$0 = \emptyset$ $1 = \{\emptyset\}$ $2 = \{\emptyset, \{\emptyset\} \}$ $3 = \{ \emptyset, \{\emptyset\}, \{\emptyset, \{\emptyset\}\}\}$ … Vždy platí, že číslo n vyjadríme ako $n = \{0, 1,..., n-1\}$ .

Celé čísla

Celé čísla $Z = \{...,-3,-2,-1,0,1,2,3,...\}$ konštruujeme nasledovným spôsobom:
Definujeme na množine $N_{\small 0}\ \times \ N_{\small 0}$ relaci $\sim$ vzťahom:
$(a,b)\ \sim \ (c,d) \Leftrightarrow a + d = c + b$ Jedná sa o relaci ekvivalence, ak položíme $Z = N_{\small 0}\ \times \ N_{\small 0} / \sim$ , dostaneme rozklad množiny. Triedu ekvivalence $\sim$ určenú prvkom $(a,b)$ označíme $\overline{(a,b)}$ (reprezentuje rozdiel a-b). Definujeme operácie:

$\overline{(a,b)} + \overline{(c,d)} = \overline{(a+c,b+d)}$

$\overline{(a,b)} \cdot \overline{(c,d)} = \overline{(ac+bd,ad+bc)}$

$- \overline{(a,b)} = \overline{(b,a)}$

(tip: operácie sa ľahko pamätajú, ak si pod $\overline{(a,b)}$ predstavíte $a-b$ )
Uvedené definície nezávisia na voľbe reprezentantov ⁸⁾. Prirodzenému číslu n odpovedá celé číslo $\overline{(n,0)}$

Racionálne čísla

Na množine $Z\ \times \ Z^{*}$ ( $Z^{*}$ značí množinu nenulových celých čísel) definujeme relaci $\sim$ vzťahom:
$(a,b)\ \sim \ (c,d) \Leftrightarrow ad = cb$ Jedná sa o relaci ekvivalence, ak položíme $Q = (Z\ \times \ Z^{*}) / \sim$ , dostaneme rozklad množiny. Triedu ekvivalence $\sim$ určenú prvkom $(a,b)$ označíme $\overline{(a,b)}$ (reprezentuje zlomok $\frac{a}{b}$ ). Definujeme operácie:

$\overline{(a,b)} + \overline{(c,d)} = \overline{(ad+bc,bd)}$

$\overline{(a,b)} \cdot \overline{(c,d)} = \overline{(ac,bd)}$

(tip: operácie sa ľahko pamätajú, ak si pod $\overline{(a,b)}$ predstavíte $\frac{a}{b}$ )
Pre $a,b \neq 0$ platí $\overline{(a,b)}^{-1} = \overline{(b,a)}$ . Celému číslu a odpovedá racionálne číslo $\overline{(a,1)}$ .

Reálne čísla

Konštrukcia reálnych čísiel je trochu zložitejšia, preto tu nebudem uvázdať celý postup. Je nutné definovať usporiadanie na množinách Z a Q a následne definovať operácie pomocou rezov množiny Q. R definujeme ako množinu všetkých rezov, ktoré sú buď mezery (iracionálne čísla) alebo dedekindovské rezy 1.druhu (racionálne čísla). Viac informácií nájdete v skriptách ⁹⁾.

Komplexné čísla

Množinu komplexných čísel C chápeme ako množinu všetkých dvojíc reálnych čísel, teda $C = R \times R$ . Pre ľubovoľné $(a,b),\ (c,d)\in C$ definujeme operácie sčítania a násobenia:

$(a,b)+(c,d) = (a+c,b+d)$

$(a,b)\cdot (c,d) = (ac-bd,ad+bc)$

Ak komplexné číslo (0,1) označíme i a (t,0) t, môžeme každé komplexné číslo $z= (a,b)$ písať v tvare:
$z= a+bi$ (algebraický tvar, a - reálna časť, b -imaginárna časť)
Pre imaginárnu jednotku platí $i^2 = -1$ , to nám dovoľuje riešiť aj také rovnice (napr. $x^2 + 1= 0$ ), ktoré v obore reálnych čísel nemajú riešenie.
Z algebraického tvaru a ze vztahu $i^2 = -1$ pak můžeme zpětně rekonstruovat násobení komplexních čísel: $(a,b)\cdot(c,d) = (a+bi)\cdot(c+di) = ac-bd + adi+bci = (ac-bd, ad+bc)$

Co byste ještě měli znát?

Měli byste chápat a být schopni vysvětlit rozdíl mezi minimálním a nejmenším prvkem.
Měli byste být schopni sami uvést příklady svazu, úplného svazu nebo nelineárního uspořádání.
Ale také byste měli být schopni určovat supréma, infima pro množiny zadané komisí a měli byste umět určit, zda je daná množina svaz, úplný svaz apod.

Predmety

FI:MB005 Základy matematiky (podzim 2005), Mgr. Ondřej Klíma, Ph.D.
FI:IB000 Úvod do informatiky (podzim 2005), prof. RNDr. Antonín Kučera, Ph.D.

Použitá literatúra

skriptá Úvod do informatiky, prof. RNDr. Antonín Kučera, Ph.D. (odkaz som nenašiel)
Mgr. Jan Holeček riešené príklady 6.sada (dostupné pouze z domény muni.cz)
Učebné materiály k MB005
Uspořádání, skripta pro ÚdoI, doc. RNDr. Petr Hliněný, Ph.D.

Vypracoval

Dušan Katona, ICQ: 426 081 873, snad do 27.5
hotovo: <99%>
môžete kluďne niečo doplniť alebo opraviť

Otázku si přečetl pan RNDr. Jan Bouda a rámcově prošel. Jeho podněty pro doplnění textu, opravy nesrovnalostí a odstranění matoucích či k otázce se nevztahujících textů byly do otázky zaneseny. Tato kontrola je jen rámcová, stále se může stát, že v otázce zůstala zapomenutá chybka či nesrovnalost, vyučující za toto nenese odpovědnost, berte tuto rámcovou kontrolu jako formu pomoci od vyučujících pro studenty.

¹⁾

Základy matematiky skriptá, str. 13

²⁾

riešené príklady od Mgr. Jana Holečka, 6. sada

³⁾

www.cam.zcu.cz/~ryjacek/students/DMA/skripta/3.pdf

⁴⁾

Základy matematiky skriptá, str. 14

⁵⁾

http://user.mendelu.cz/marik/in-mat-web/in-mat-webse18.html

⁶⁾

skriptá RNDr. Pavla Horáka

⁷⁾

Algebra v obrázcích - http://algebra.matfyz.info/

⁸⁾

Základy matematiky skriptá, str. 12

⁹⁾

Základy matematiky skriptá, str.17