Obsah

AP4, IN4 Výroková logika
Diskuze

AP4, IN4 Výroková logika

Zadání

IN(syntax, sémantika, odvozovací systém výrokové logiky, důkazy ve výrokové logice, pravdivost a dokazatelnost logických formulí)

AP(syntax, sémantika, odvozovací systém výrokové logiky, důkazy ve výrokové logice, pravdivost a dokazatelnost logických formulí, rezoluce)

Vypracování

Logika

Logika se zabývá problematikou správnosti usuzování (vztah vyplývání). Na usuzování však logiku zajímají pouze vybrané aspekty. Usuzování chápeme jako určitý myšlenkový proces. Psychologické aspekty tohoto procesu však logika zcela opomíjí, stejně jako jeho obsahovou stránku. Zabývá se především analýzou formální stavby úsudků jako základních jednotek usuzování. Úsudkem rozumíme takový myšlenkový postup, kterým dospíváme od nějakých tvrzení, která nazýváme předpoklady (premisy), k jinému tvrzení, které nazýváme závěr (důsledek). Při studiu úsudků logiku zajímá pouze jejich forma, nikoliv konkrétní obsah. Proto úsudkem je z hlediska logiky schéma tvaru:

A₁, A₂, …, A_n / B,

kde výrazy A₁, A₂, …, A_n reprezentují nějaká tvrzení a výraz B tvrzení, které je závěrem. Je-li úsudek daného tvaru platný (z pravdivých premis vždy získáme pravdivý závěr), říkáme, že závěr B vyplývá z premis A₁, A₂, …, A_n (A₁, A₂, …, A_n implikuje B [2]).[1]

Logika je schopna (svými prostředky) kontrolovat správnost pouze u deduktivních úsudků. Porovnejte následující dva úsudky:

všichni lidé jsou smrtelní, Sokrates je člověk;
tudíž Sokrates je smrtelný

slunce doposud vyšlo každý den;
tudíž (asi) vyjde i zítra.[1]

První z nich je běžný příklad deduktivního úsudku, který je považován za platný. Druhý úsudek je považován za deduktivně neplatný — je to pravděpodobnostní úsudek.
Rozdíl mezi deduktivními a pravděpodobnostními úsudky je mj. v tom, že u platného deduktivního úsudku je pravdivost závěru zaručena pravdivostí premis, kdežto u pravděpodobnostního úsudku pravdivost premis nezaručuje jistou pravdivost závěru, pouze jeho pravděpodobnost (v uvedeném úsudku je tato pravděpodobnost jistě vysoká). [1]

Logika poskytuje nástroj pro budování (vědeckých) teorií (teorie grup, modální logiky). Například výpočtová logika umožňuje automatizaci důkazů a programování v jazyce Prolog (logické programování). [2]

Klasifikace logik

Nejobecnější klasifikací usuzování vůbec je rozdělení na:

Mentální (neformální) – usuzování všeobecně („selský rozum”), to co je poznatelné
Formální – to co je poznané a definované, metody odvozování.
- Rozlišujeme dvouhodnotovou a vícehodnotovou logiku podle toho, zda připouštíme k ohodnocení tvrzení právě dvě pravdivostní hodnoty, tj. „pravda“ a “nepravda“, nebo více než dvě pravdivostní hodnoty.
- Dále rozlišujeme logiku extenzionální a intensionální především podle toho, jakých spojek se užívá pro vytvoření složených tvrzení. U extenzionální pravdivost formule závisí jen na pravdivosti jejich složek („ne“, „a“, „nebo“), naopak u intensionální („možná“, „věřím“…).
- Logika, která je dvouhodnotová a extenzionální se nazývá klasická logika. Dělí se dále podle detailnosti analýzy na logiku výrokovou a predikátovou.

Klasická logika

Výroková logika

„Nebude-li pršet nezmoknem“ $(p \wedge \neg q \Rightarrow r)$ . Více viz. níže.

Predikátová logika
- 1. řádu: „Není pravda, že všichni lidé jsou spokojení.“ $\neg\forall x: (clovek(x) \Rightarrow spokojeny(x))$
- 2. řádu: „Existuje vlastnost, kterou mají všichni lidé.“ $\exists P \forall x: (clovek(x) \Rightarrow P(x))$

[1] a [2]

Metajazyk

Žádný jazyk nelze systematicky vybudovat pouze pomocí jeho vlastních výrazových prostředků. K tomuto účelu vždy potřebujeme další jazyk (vyšší expresivní úrovně), v němž pak také můžeme formulovat výpovědi o výrazech toho nového jazyka. Jazyk který budujeme, nazveme objektový jazyk a jazyk, ve kterém hovoříme o objektovém jazyce, nazveme metajazyk. Nerozlišování objektového jazyka a metajazyka vede ke vzniku tzv. sémantických paradoxů. Např. paradox lháře: „Tato věta je nepravdivá“.[1]

Výroková logika

Výroková logika je teorií logických spojek chápaných jako pravdivostní funkce. [1] Zabývá se způsoby tvoření výroků pomocí spojek a vztahy mezi pravdivostí různých výroků. [2]

Nezabývá se smyslem výroků, jelikož má extenzionální charakter. Výroková logika zkoumá uvedené jevy prostřednictvím umělého jazyka používajícího výrokových symbolů, logických spojek a závorek. Jelikož sémantika tohoto jazyka je extenzionální, lze si představit, že výroková logika uznává pouze dva výroky: jeden, který reprezentuje všechny pravdivé výroky a druhý, který reprezentuje ty nepravdivé. [1]

Syntax

Výroková logika rozlišuje na syntaktické úrovni dva typy výroků — jednoduché (elementální) a složené:

Výrok je tvrzení nebo jazykový výraz, o jehož (ne)pravdivosti lze uvažovat.[1] Jednoduchý výrok je výrok, který neobsahuje žádnou logickou spojku. Složený výrok je výrok, který obsahuje alespoň jednu logickou spojku.[2]

Příklady:

Výroky:

je pět hodin
2 + 3 = 5
pokud nenapíšeš úkoly a neuklidíš, nepůjdeme do kina

Výrazy, které nejsou výroky:

Kolik je hodin?
2 + 3
napiš úkoly a ukliď

[2]

Pravdivostní spojky (funkce)

Pravdivostní hodnota složeného výroku je jednoznačně určena pravdivostními hodnotami složek. Uvažujeme-li n-ární spojku, pak tato spojka je funkcí, která přiřazuje n-tici pravdivostních hodnot určitou pravdivostní hodnotu. Počet pravdivostních hodnot je konečný, jsou dvě (pravda, nepravda).[1]

Každou n-ární spojku (jako pravdivostní funkci) lze zadat tabulkou o 2ⁿ řádcích, tzv. pravdivostní tabulkou.[1]

Počet vzájemně různých n-árních spojek je $2^{2^n}$ [1].

Nulární výrokové spojky

Nulární pravdivostní funkce (nezávisí na žádném argumentu) jsou konstanty odpovídající pravdivostním hodnotám 0,1. [2]

Unární (jednoargumentové) výrokové spojky

p		F₁	F₂	F₃	F₄
1		1	1	0	0
0		1	0	1	0

F₁: unární verum,
F₂: unární projekce p,
F₃: negace p (ozn. ¬p);jediná netriviální unární funkce,
F₄: unární falsum.
[1],[2]

Binární výrokové spojky

Přehled nejpoužívanějších spojek:

p	q	$\vee$	$\wedge$	$\Rightarrow$	$\Leftrightarrow$	F₅	F₆	F₇
1	1	1	1	1	1	0	0	0
1	0	1	0	0	0	1	1	0
0	1	1	0	1	0	1	1	0
0	0	0	0	1	1	1	0	1

$\vee$ — disjunkce (alternativa; a nebo; OR)
$\wedge$ — konjunkce (a zároveň; AND)
$\Rightarrow$ — implikace (jestliže p, pak q; předpoklad $\Rightarrow$ důsledek)
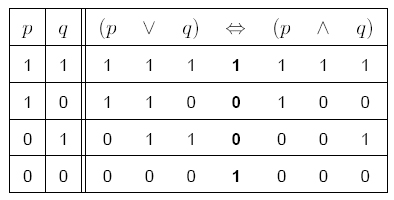
$\Leftrightarrow$ — ekvivalence (právě tehdy,když;iff - if and only if)
F₅ — Shefferova funkce (negace konjunkce;NAND;„… je neslučitelné s …“)
F₆ — nonekvivalence (spojka nebo ve vylučovacím smyslu;„buď …,anebo …“;XOR - eXclusive OR)
F₇ — Nicodova (Peirceova) funkce (negace disjunkce;NOR;„ani …, ani …“)

Spojky $\vee , \wedge$ jsou komutativní (hodnota funkce nezávisí na pořadí argumentů).
Běžně se používá infixový zápis $(p \vee q)$ .
$\Leftrightarrow$ je komutativní, $\Rightarrow$ není komutativní.

[1],[2]

Symbolický jazyk výrokové logiky

Jazyk výrokové logiky má tuto abecedu a gramatiku:

Abeceda:
1. Výrokové symboly: p, q, r, s ,případně p₁, p₂, …
2. Symboly pro spojky: $\neg , \vee , \wedge , \Rightarrow , \Leftrightarrow$
3. pomocné symboly: (, ), [, ], {, }
Gramatika sestává z pravidel:
1. každý výrokový symbol je správně utvořenou formulí výrokové logiky (ve zkratce s. u. f. VL) — tzv. atomická formule;
2. je-li výraz A s. u. f. VL, pak výraz ¬(A) je s. u. f. VL;
3. jsou-li výrazy A a B s. u. f. VL, pak také výrazy (A) $\vee$ (B), (A) $\wedge$ (B), (A) $\Rightarrow$ (B), (A) $\Leftrightarrow$ (B) jsou s. u. f. VL;
4. jen výrazy utvořené podle 1,2,3 jsou s. u. f. VL.

[1]

Symboly A a B z bodů 2 a 3 této induktivní definice jsou výrazy metajazyka. Nepatří tedy do jazyka výrokové logiky, ale označují jeho libovolné výrazy (správně utvořené formule). Závorky lze vynechat, pokud odstraněním nedojde k nejednoznačnostem.[1]

Reprezentace výroků v přirozeném jazyce

Věta:„Pokud rychle napíšeš úkoly a venku bude hezky, půjdeme na procházku nebo pojedeme na koupaliště.“

p — „rychle napíšeš úkoly“
r — „venku bude hezky“
s — „půjdeme na procházku“
t — „pojedeme na koupaliště“

Výsledná reprezentace v symbolickém jazyce je: $(p \wedge r)\Rightarrow(s \vee t)$

Převod z přirozeného jazyka do symbolického jazyka výrokové logiky nemusí být vždy jednoznačný.

[2]

Sémantika

Pravdivostní ohodnocení (interpretace) je funkce přiřazující všem atomickým formulím dané úvahy pravdivostní hodnoty (tj. každému výrokovému symbolu přiřadí 0 nebo 1). Valuace je rozšíření interpretace z atomických na všechny formule dle tabulky pro výrokové spojky.

Interpretace I splňuje formuli A (formule je pravdivá v I, resp. odpovídající valuace I'(A) = 1), pokud

A je výrokový symbol a I(A) = 1
A je $\neg B$ a I nesplňuje B, resp. I'(B) = 0
A je tvaru $B \wedge C$ a I splňuje B i C, resp. I'(B) = I'(C) = 1
A je tvaru $B \vee C$ a I splňuje B nebo C, resp. I'(B) = 1 nebo I'(C) = 1
A je tvaru $B \Rightarrow C$ a I nesplňuje B nebo splňuje C, resp. I'(B) = 0 nebo I'(C) = 1
A je tvaru $B \Leftrightarrow C$ a I splňuje B i C nebo I nesplňuje B i C, resp. I'(B) = I'(C)

[2]

Formule A se nazývá tautologie, je-li splňována každou interpretací. Např. $\neg p \vee p$
Formule A se nazývá kontradikce, jestliže není splňována žádnou interpretací. Např. $\neg p \wedge p$
Říkáme, že formule A je splnitelná, je-li splňována aspoň jednou interpretací I, kterou pak nazýváme model formule A. Množina formulí T je splnitelná, jestliže existuje ohodnocení I takové, že každá formule A ∈ T je splňována I. Tuto interpretaci pak nazýváme model množiny T. Říkáme, že formule A logicky vyplývá (na základě výrokové logiky) z množiny T a tuto skutečnost označíme $T \vdash A$ (případně T ∴ A), jestliže pro každý model I množiny T je formule A interpretací I splňována.

Tautologií je nekonečně mnoho.[2]

Ke zjištění pravdivosti formulí pro všechny možné interpretace používáme tabulkovou metodu.
[2]
Zásady:
Vyhodnocení probíhá po složkách (podformulích) dané formule (výrok. symboly, negace, …, celá formule).
Zápis pravdivostní hodnoty provedeme v řádku s příslušnou interpretací pod vyhodnocovanou spojkou (výr. symbol).[2]

Odvozovací systém výrokové logiky

Formální systém výrokové logiky

Na rozdíl od vyhodnocování (interpretace, resp. valuace) logických formulí na základě atomických formulí (výrokových symbolů) klademe na formální systém výr. logiky požadavek na dokazování výr. formulí. Tj. zjištění, zda-li pravdivost dané formule vyplývá z pravdivostí jiných formulí.

Formálním systémem výrokové logiky se rozumí jazyk výrokové logiky a deduktivní soustava, která je tvořena odvozovacími pravidly a případně axiomy. Za axiomy (výchozí tvrzení přijímaná bez důkazu) volíme vhodná schémata tautologií, odvozovací pravidlo chápeme jako operace na formulích umožňující konstrukce důkazů a stačí jediné - pravidlo modus ponens. Po tomto pravidle požadujeme korektnost, to znamená, aby z pravdivých premis byl odvozen pravdivý závěr. Formální systémy jsou postaveny výhradně na syntaktické bázi, jazyk logiky neinterpretujeme, provádíme s ním pouze syntaktické manipulace — důkazy.[2]

Formální systémy lze rozdělit na:

axiomatické (méně pravidel)
předpokladové (méně axiomů) — např. Gentzenovský systém (kalkul sekventů), jediný axiom ( $A \vdash A$ ). Důkaz sekventu je strom, v jehož kořeni je dokazovaný sekvent, v listech axiomy a každý uzel (závěr) se svými přímými následovníky (předpoklady) představuje instanci některého z pravidel systému.

Požadované vlastnosti formálních systémů:

korektnost (bezespornost): je dána výběrem axiomů a odvozovacích pravidel; systém je korektní, nelze-li v něm zároveň odvodit tvrzení i jeho negaci. Ve sporném systému lze odvodit cokoliv. Vyžadována vždy.
úplnost: připojením neodvoditelné věty k úplnému systému se tento stane sporným. Nevyžadována vždy – úplné jsou pouze velmi jednoduché teorie.
rozhodnutelnost: existence algoritmu pro ověření dokazatelnosti libovolné formule. V axiom. systémech podmíněna úplností; zpravidla splněna pouze pro určité třídy formulí.
nezávislost axiomů: nezávislý axiom nelze odvodit z ostatních axiomů;závislý axiom může být vypuštěn z dané soustavy axiomů.

[1] a [2]

Modus ponens (MP)

MP je základní a nejdůležitější odvozovací pravidlo. Jeho tvar:
$\frac{A, \quad A \Rightarrow B}B$
MP říká, že když máme formule A a A ⇒ B pak z toho vyplývá platnost B.

Důkazy ve výrokové logice

Důkaz je v daném systému konečná posloupnost správně utvořených formulí (kroků důkazu), z nichž každá je buď axiómem nebo byla odvozena aplikací některého pravidla odvození na některé předcházející správně utvořené formule. Určitá formule je dokazatelná v daném systému tehdy a jen tehdy, když v tomto systému existuje důkaz, jehož je tato formule členem. ( $\vdash$ ). Teorém je v systému S formule, která je dokazatelná v systému S.[3]

Pravdivost a dokazatelnost logických formulí

Pravdivost logické formule je dána sémantikou této formule. Kdežto,
dokazatelnost (odvoditelnost) logické formule je posuzována syntaxí. Říkáme, že formule je dokazatelná, pokud k této formuli existuje důkaz. Těchto důkazů je nekonečně mnoho.

Rezoluce

Rezoluce je formální systém výrokové logiky vhodný pro strojové dokazování (Prolog) a je založena na vyvracení — dokazuje se nesplnitelnost formulí. Rezoluce pracuje s formulemi v KNF¹⁾, notace je však jiná:

klauzule je konečná množina literálů (chápána jako jejich disjunkce). Je pravdivá, pokud alespoň jeden prvek je pravdivý. Prázdná klauzule □ je vždy nepravdivá — neobsahuje žádný pravdivý prvek. Příklad klauzule $\{p, \neg q, r\}$ dříve značeno $(p \vee \neg q \vee r)$ .
formule je (ne nutně konečná) množina klauzulí (chápána jako jejich konjunkce, tedy KNF). Je pravdivá, je-li každý její prvek pravdivý. Prázdná formule ∅ je vždy pravdivá — neobsahuje žádný nepravdivý prvek. Příklad formule $\{\{ \neg q\},\{ \neg p, q\}\}$ dříve značeno $\neg q \wedge ( \neg p \vee q)$ .
rezoluční pravidlo: nechť $C_1 \ = \ \{p\} \ \sqcup \ C'_1, \ C_2 \ = \ \{ \neg p \} \ \sqcup \ C'_2$ jsou klauzule, jejich rezolventou je $C \ = \ C'_1 \ \cup \ C'_2$ . Rezoluční pravidlo zachovává splnitelnost, tj. libovolná valuace splňující C₁ a C₂ splňuje i C.
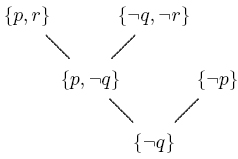
rezoluční důkaz klauzule C z formule S je konečná posloupnost klauzulí C₁,C₂,…,C_n, kde C_n = C a každé C_i je buď prvkem S, nebo rezolventou klauzulí C_j, C_k pro j,k < i. Existuje-li tento důkaz, je C rezolučně dokazatelná z S (píšeme $S \ \vdash \ _R \ C$ ). Odvození □ z S je vyvrácením S.

[2]

Přehlednější reprezentací rezolučních důkazů jsou stromy. Strom rezolučního důkazu C z S je binární strom T s vlastnostmi:

kořenem T je C
listy T jsou prvky S
libovolný vnitřní uzel C_i s bezprostředními následníky C_j, C_k je rezolventou C_j, C_k.

Příklad: strom důkazu $C \ = \ \{\neg q\}\ z\ S\ =\ \{\{p,r\},\{\neg q,\neg r\},\{\neg p\}\}$

Obecné schéma důkazu, formule A je log. důsledkem množiny formulí T:

vytvoříme konjunkci T' všech prvků z T,
formuli T' ∧ ¬A převedeme do KNF a
ukážeme KNF(T' ∧ ¬A) $\vdash \ _R$ □.

Výhody pro strojové zpracování:

systematické hledání důkazu
práce s jednoduchou datovou strukturou
jediné odvozovací pravidlo

Problém: Strategie generování rezolvent — prohledávaný prostor může být příliš veliký. Omezení prohledávaného prostoru (zjemnění rezoluce):

ukončením prohledávání neperspektivních cest
určením pořadí při procházení alternativních cest

Doposud [2].

Lineární rezoluce –- jde o posloupnost dvojic $<C_{0}, B_{0}>$ , … , $<C_{n}, B_{n}>$ takovou, že $C = C_{n+1}$ a

$C_{0}$ a všechny $B_{i}$ jsou z S anebo nějaké $C_{j}$ , kde $j<i$
každé $C_{i+1}$ , $i \leq n$ je rezolventou $C_{i}$ a $B_{i}$ (vstupní klauzule S, boční $B_{i}$ a střední $C_{i}$ )

je korektní a úplná

Lineární vstupní rezoluce (LI) množiny $S=P \cup \{ G\}$ je lineární vyvrácení S, které začíná klauzulí G, a bočními klauzulemi jsou jen klauzule z P.

je úplná jen pro Hornovy klauzule²⁾

LD rezoluce –- už máme uspořádané klauzule a při rezoluci vkládáme dovnitř. LD rezoluční vyvrácení $P \cup \{ G\}$ je postupnost $<G_{0}, C_{0}>$ , … , $<G_{n}, C_{n}>$ uspořádaných klauzulí taková, že $G_{0}=G, G_{n+1}=$ □, $C_{i} \in T$ a každé $G_{i}$ , $1\leq i\leq n$ je rezolventou uspořádaných klauzulí $G_{i-1}$ a $C_{i-1}$

[4]

Předměty

IB101 Úvod do logiky a logického programování

Použitá literatura

[1] Štěpán, Jan, Klasická logika. Olomouc, Univerzita Palackého v Olomouci 2001.
[2] Popelínský, L., Mráková, E., Úvod do logiky a logického programování, slídy, červen 2008, dostupné na: http://www.fi.muni.cz/~popel/lectures/bak_logika/
[3] Raclavský, J., Výroková logika, červen 2008, dostupne na http://www.phil.muni.cz/fil/logika/vl.php
[4] Vypracování otázek Elena Halická - http://www.fi.muni.cz/~xhalic1/statnice/vypracovaneIM.doc

Kam dál?

Volně stažitelné skripta z předmětu Výroková a predikátová logika na MFF UK od Petra Štěpánka

Vypracuje

Erik Zitterbart, ICQ: 172319825. eriksson (zavinac) mail.muni.cz
Z mé strany 99%. Rád dopracuji případné komentáře a opravy. Vypracování je poněkud delší.

Otázku si přečetl pan doc. RNDr. Lubomír Popelínský a rámcově prošel. Jeho podněty pro doplnění textu, opravy nesrovnalostí a odstranění matoucích či k otázce se nevztahujících textů byly do otázky zaneseny. Tato kontrola je jen rámcová, stále se může stát, že v otázce zůstala zapomenutá chybka či nesrovnalost, vyučující za toto nenese odpovědnost, berte tuto rámcovou kontrolu jako formu pomoci od vyučujících pro studenty.

¹⁾

Konjunktivní Normální Forma

²⁾

klauzule s nejvýše jedním pozitivním literálem