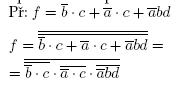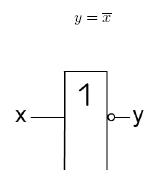Obsah
====== AP1, IN1
Výpočetní systémy I
Zadání
=
IN (číselné soustavy, vztahy mezi číselnými soustavami, zobrazení čísel v počítači, principy provádění aritmetických operací. Booleova algebra, kombinační a sekvenční logické obvody)
AP (číselné soustavy, vztahy mezi číselnými soustavami, zobrazení čísel v počítači, principy provádění aritmetických operací. Booleova, Shefferova a Piercova1) algebra, kombinační a sekvenční logické obvody.)
===== Číselné sou
stavy
je způsob reprezentace čísel. Podle způsobu určení hodnoty čísla z dané reprezentace rozlišujeme dva hlavní druhy číselných soustav: poziční číselné soustavy a nepoziční číselné soustavy. V praxi se však také používaly způsoby reprezentace používající postupy z obou těchto druhů. Dnes se obvykle používají soustavy poziční.
Nepoziční číselná soustava
je způsob reprezentace čísel, ve kterém není hodnota číslice dána jejím umístěním v dané sekvenci číslic. Tyto způsoby zápisu čísel se dnes již téměř nepoužívají a jsou považovány za zastaralé.
V nejjednodušším systému stačí sečíst hodnoty jednotlivých číslic. Pokud by například byly hodnoty symbolů následující: A = 1, B = 10, C = 100, D = 1000, pak by vyjádřením čísla 3542 mohl být například řetězec „AABBBBCCCCCDDD“.
Dalším příkladem nepoziční číselné soustavy je počítání na prstech.
==== Poziční číselné s
oustavy ====
je dnes převládající způsob písemné reprezentace čísel – dokonce, pokud se dnes mluví o číselných soustavách, jsou tím obvykle myšleny soustavy poziční. V tomto způsobu zápisu čísel je hodnota každé číslice dána její pozicí v sekvenci symbolů. Každá číslice má touto pozicí dánu svou váhu pro výpočet celkové hodnoty čísla.
Polyadické soustavy
Polyadické soustavy jsou speciálním případem pozičních soustav.
Základ – počet symbolů pro číslice používaných v dané soustavě
Řád -– váha číslice
zápis
číslo = součet mocnin základu vynásobených číslicemi
A = an · zn + an−1 · zn−1 + · · · + a1 · z1 + a0 · z0
A = 1 · 102 + 2 · 101 + 3 · 100
zhuštěný zápis
běžná je forma zhuštěného zápisu:
A = anan−1 . . . a1a0
A = 123
A = 12310
• Zobecnění pro racionální číslo (zavedeme záporné mocniny): A = an · zn +· · ·+a0 · z0 +a−1 · z−1 +a−2 · z−2 +· · ·+a−m · z−m
• Zobecnění pro záporná čísla – přidáním znaménka (pro počítače nevhodné)
• Zobecnění pro komplexní čísla – zavedením imaginární jednotky
Příklad číselné soustavy se základem 2 (tj. dvě číslice 1,0) a výpočet jeho hodnoty:
(10010)2 = 0 · 20 + 1 · 21 + 0 · 22 + 0 · 23 + 1 ·24
==== Soustavy užívané v počítačové pra
xi ====
Dvojková (Binární) - z = 2; obsahuje číslice: 0, 1
Osmičková (Oktalová) - z = 8; obsahuje číslice: 0, 1, 2, 3, 4, 5, 6, 7
Šestnáctková (Hexadecimální) - z = 16; obsahuje číslice: 0, 1, . . . 9, A, . . . , F
Vztahy mezi číselnými soustavami
Číslo
v soustavě o základu zk (kde z a k jsou přirozená čísla) lze převést do soustavy o základu z jednoduše.
Převody
| 2 ←→ 8 | 8 ←/→ 16 |
| 2 ←→ 16 | 2 ←/→ 10 |
Každou k-tici číslic nižší soustavy nahradíme číslici soustavy vyšší.
Např. 0011 1011 01002 = 3B416
Převod z 10 soustavy do 2 12,210 = ?2 Rozdělit na celou a desetinnou část čísla:
| 12 | : 2 |
| 6 | 0 |
| 3 | 0 |
| 1 | 1 |
| 0 | 1 |
| 0, | 2 · 2 |
| 0 | 4 |
| 0 | 8 |
| 1 | 6 (0,6 · 2) |
| 1 | 2 (0,2 · 2) |
| 0 | 4 |
| 0 | 8 |
| 1 | 6 |
| . . . | . . . |
12,210 = 1100,0011001100… 2
Převod z 2 soustavy do 10
1100,00110011002 = ?10
Celá část:
1 · 23 + 1 · 22 + 0 · 21 + 0 · 20 = 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 = 12
Desetinná část:
0 · 2−1 + 0 · 2−2 + 1 · 2−3 + 1 · 2−4 + 0 · 2−5 + 0 · 2−6 + 1 · 2−7 + 1 · 2−8 + … = 0 · 0,5 + 0 ·
0,25 + 1 · 0,125 + 1 · 0,0625 + … = 0,19999…
Rešení: zaokrouhlení dle poslední číslice rozvoje.
Zobrazení čísel v počítači
Zobrazení celého čísla v počítači v binárním tvaru
1) Zobrazení kladných čísel
rozsah zobrazení bez použití znaménkového bitu: < 0; 2n − 1 >
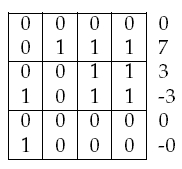
Zobrazení např. na 4 bitech (n = 4):
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 8 | |
| 1 | 0 | 0 | 1 | 9 | |
| 1 | 1 | 1 | 1 | 15 | |
rozsah zobrazení při použití znaménkového bitu: < 0; 2n-1 − 1 > 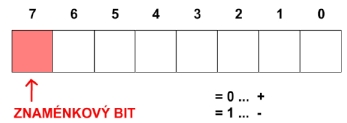
2) Zobrazení záporných čísel
a) Přímý kód se znaménkem
b) Inverzní kód
rozsah zobrazení je < −2n-1+ 1;−0 >
první bit tedy určuje zápornost
záporná čísla se invertují, tedy:  pozor! existence dvou nul → -0 a 0
pozor! existence dvou nul → -0 a 0
c) Doplňkový kód
Pro zápis kladného čísla jen převedeme číslo do dvojkové soustavy stejně, jako číslo bez znaménka.
U doplňkového kódu vyřešen problém dvou nul.
Postup pro zobrazování záporných čísel v doplňkovém kódu:
1. zobrazit kladné číslo v binární soustavě
2. prohodit 1 a 0 v zápise binárního čísla
3. přičíst 1
příklady: Př. 1: převedeme číslo (-55) do doplňkového kódu (na 16 bitů):
(55) = (0000 0000 0011 0111)
prohodíme jedničky a nuly a přičteme 1:
(-55)10 = 1111 1111 1100 1000 +1 = (1111 1111 1100 1001)DK
Př. 2: převedeme číslo (-1023) do doplňkového kódu (na 16 bitů):
(-1023)10 = 1111 1100 0000 0000 +1 = (1111 1100 0000 0001)DK
d) Kód s posunutou nulou
V kódu s posunutou nulou využíváme bázi posunutí (standardně 27 - 1). K této bázi přičteme požadované číslo a výsledek zobrazíme.
příklad:
číslo (55) zobrazte na 8 bitů:
27 - 1 +55 = 128 - 1 + 55 = 182 = (10110110)
analogicky záporné číslo (-55) na 8 bitů:
27 - 1 -55 = 128 - 1 - 55 = 72 = (1001000)
Zobrazení reálného čísla v jednoduché přesnosti
Zobrazení reálných nebo příliš velkých celých čísel se provádí v pohyblivé řádové čárce. Čísla jsou zobrazena ve tvaru:
č = M · zE, kde
M … mantisa čísla, zobrazená v soustavě o základu z
E … exponent z … základ pro výpočet exponentové části
Jedním z používaných formátů pro zobrazení čísel v pohyblivé řádové čárce je formát podle standardu IEEE 754 (Institute of Electrical and Electronic Engineers) používaný v moderních počítačích.
Struktura čísla:
| znaménkový bit (1 b) | exponent (8 b) | mantisa (23 b) |
Znaménkový bit
- kladné číslo má znaménkový bit nulový, u záporného čísla je tento bit jedničkový
Exponent
- je uložen na 8 bitech v kódu s posunutou nulou, báze posunutí je 27 - 1 = 127
- příklad: exponent 410 je uložen jako 4 + 127 = 131 = 1000 00112
Mantisa
- je znázorněna 24 bity v přímém kódu
- první bit (na nulté desetinné pozici) se neukládá, bere se implicitně jako 1 (mantisa se tedy ukládá počínaje druhým bitem)
- myšlená desetinná tečka je umístěna za nejvyšším bitem mantisy
- příklad: mantisa 1,562510 je desetinné číslo 1 + 0,5 + 0,0625 = 20 + 2-1 + 2-4 = 1,10012 a uloží se jako 100 1000 0000 0000 0000 0000
Příklad Zobrazte číslo (-258,125)10 ve formátu IEEE (na 4 bytech):
(258)10 = (100000010)2 0,125 · 2 = 0,25 0 0,25 · 2 = 0,5 0 0,5 · 2 = 1,0 1 (0,125)10 = (0,001)2
(258,125)10 = (100000010,001)2
Nyní je nutné provést normalizaci – pomocí násobku čísla s mocninami dvojky číslo převést do intervalu [1, 2):
nenormalizované = normalizované · 2n, kde n je hledaná mocnina.
norm. tvar: 1,00000010001 · 28 exponent: 27 - 1 + 8 = 27 + 7 = 10000000 + 111 = (10000111)
Jelikož se předpokládá normální tvar, jednotka na místě před desetinou čárkou se nezapisuje:
(-258,125)10 = (1100 0011 1000 0001 0001 0000 0000 0000)IEEE
Další příklad je možné nalézt na COMP 2300 -- IEEE 754 Example. Podrobnější popis se nachází na anglické Wikipedii. K dispozici je také testovací aplet a převodník.
Příklady zobrazení čísel:
Př. 1:
Převeďte číslo 11010011 z přímého kódu se znaménkem do desítkové soustavy.
11010011 → (64 + 16 + 2 + 1) = -83
Př. 2:
Převeďte číslo 10111001 z doplňkového kódu do desítkové soustavy.
10111001 → 01000111 = 64 + 4 + 2 + 1 = -71
Př. 3:
Převeďte číslo 01000111 z kódu s posunutou nulou do desítkové soustavy.
01000111 = 64 + 4 + 2 + 1 → -127 + 71 = -56
Př. 4:
Převeďte číslo 0100 0011 1000 0001 0001 0000 0000 0000 z formátu IEEE (na 4 bytech) do desítkové soustavy.
0 100 0011 1000 0001 0001 0000 0000 0000
Exponent:
1000 0111 → -127 + 135 = 8, tedy základ je 28 = 256
Mantisa:
1,0000 0010 0010 0000 0000 0000 (připojení implicitního bitu)
1,000000100012 = 20 + 2-7 + 2-11 = 1 + 0,0078125 + 0,00048828125 = 1,0083007812510 (jedničkové bity jsou na nultém, sedmém a jedenáctém desetinném místě)
Výsledek:
1,00830078125 · 256 = +258,125
Principy provádění aritmetických operací
Součet doplňkového kódu:
všechny bity se sčítají stejně
vznikne-li přenos ze znaménkového bitu, tak se ignoruje
přetečení nastane, pokud se přenos do znaménkového bitu nerovná přenosu ze znaménkového bitu
Př. přetečení:
0 110
0 101
01 1011
Součet v inverzním kódu:
problém dvou nul
nutnost provádět tzv. kruhový přenos = přičtení přenosu z nejvyššího řádu 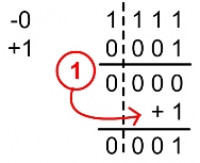
Násobení a dělení s binárními čísly se provádějí v počítačích obvykle podle stejného algoritmu jako v dekadické soustavě. Například:
5 · 3 = 15
0 1 0 1 = 5 0 0 1 1 = 3
0 1 0 1 0 1 0 1 0 0 0 0
1 1 1 1
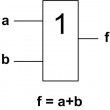
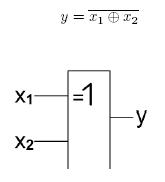
Hradlo XOR Hradlo XOR je jedním ze základních kombinačních logických obvodů, jehož výstup je exkluzívní logický součet vstupů („buď A nebo B“). Výstup je log.1 tehdy a jen tehdy pokud se hodnoty vstupů liší.
Booleova algebra
Booleova algebra je šestice (A,∧,∨,-,1,0), kde A je nazýván literál (proměnná), ∧ konjunkce, ∨ disjunkce, - negace a 1 a 0 jsou hodnoty, které literál může nabývat.
Základní pravidla:
- komutativita
- distributivita
- neutralita (
x∧1=x;y∨ 0 =y) - komplementarita (
x∨ -x= 1;y∧ -y= 0) - nedegenerovanost (1 se nerovná 0)
další pravidla:
- asociativita: (
x∨y) ∨z=x∨ (y∨z), (x∧y) ∧z=x∧ (y∧z) - absorpce:
x∨ (x∧y) =x,x∧ (x∨y) =x - agresivita nuly:
x∧ 0 = 0 - agresivita jedničky:
x∨ 1 = 1 - idempotence:
x∨x=x,x∧x=x - absorpce negace:
x∨ (−x∧y) =x∨y,x∧ (−x∨y) =x∧y - dvojitá negace: −(−
x) =x - De Morganovy zákony: −
x∧ −y= −(x∨y), −x∨ −y= −(x∧y) 0a1jsou vzájemně komplementární: −0 = 1, −1 = 0
Hornova klauzule – disjunkce, která obsahuje nejvýše jeden pozitivní literál
implikace (⇒) je dána přepisem a ⇒ b ⇔ -a ∨ b
ekvivalence je konjunkce oboustranných implikací
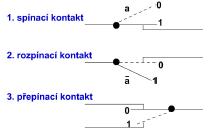
Způsob zobrazení:
- Pravdivostní tabulka
- Graficky v rovině = Vennovy diagramy (klasicky průnik množin)
- Matematický aparát (asi nejběžnější způsob, pomocí symbolů)
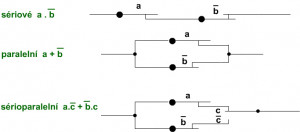
Využití Booleovy algebry:
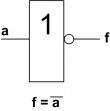
Obvodové znázornění Booleovy alebry:
Minimalizace počtu operací B-algebry:
1. Matematickými úpravami
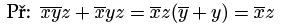 Upraví se podle výše zmíněných pravidel.
Upraví se podle výše zmíněných pravidel.
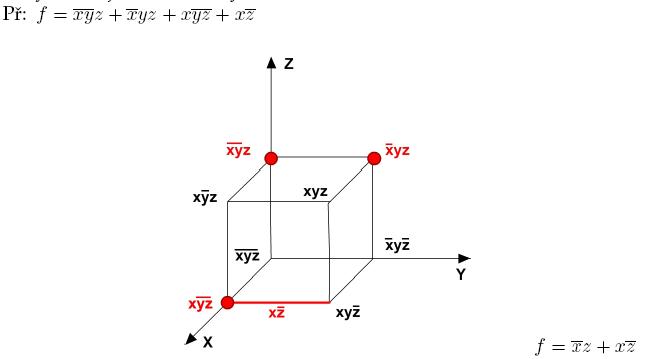
Postup
Označíme si tedy jednotlivé rohy krychle a vyznačíme naši funkci, kterou chceme minimalizovat.
Dva vybrané body si propojíme a určíme jejich společnou vlastnost. (tj. v našem případě, pokud propojíme oba horní rohy, tak ty mají společné to, že x je negováno a z není). To pak zapíšeme a spojíme s dalšími odvozeními pomocí log. spojky + (OR)
3. Karnaughova mapa (gray-kód), Svobodova mapa (binární kód)
Příklady zakreslení funkcí do karnaughovy mapy (postupně 2 řád, 3 řád a 4 řád) 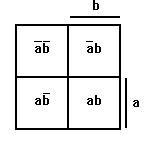
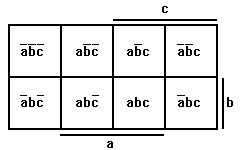
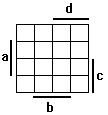 Pro vyšší řády nejsou souvislé prostory proměnných.
Pro vyšší řády nejsou souvislé prostory proměnných.
Příklad minimalizace funkce pomocí karnaughovy mapy: 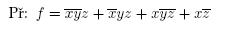
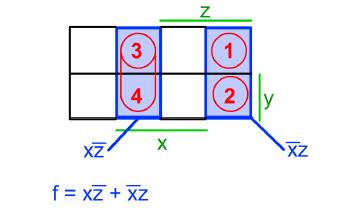
Postup
4. Další minimalizační algoritmy (Quine-McCluskey, TANT…) – vhodné pro větší počet vstupních proměnných, strojové zpracování.
Shefferova algebra
Je vybudována na jedné logické funkci = negace logického součinu NAND
Pravidla: 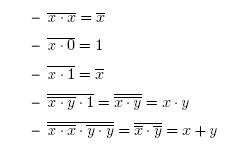
Pomocí operace NAND lze realizovat všechny Booleovské výrazy
Platí zákon komutativnosti 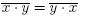 NEPLATÍ asociativnost:
NEPLATÍ asociativnost: 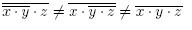
Peirceova algebra
Vystavěna na operaci NOR (negace logického součtu) - obdobně jako S-algebra.
Převod minimalizované formy B-algebry na S-algebru:
Opakovanou aplikací de Morganových pravidel 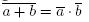
Kombinační a sekvenční logické obvody
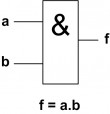
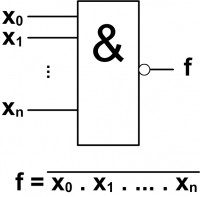
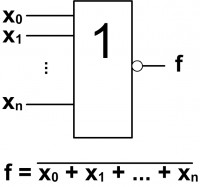
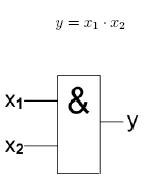
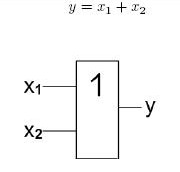
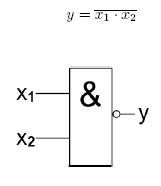
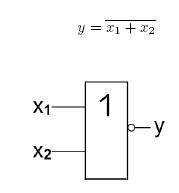
Kombinační logické obvody - základní logické členy:
Sekvenční logické obvody:
Sekvenční obvod je typ elektronického obvodu. Je složen ze dvou částí – kombinační a paměťové. Abychom mohli určit hodnotu výstupní proměnné, je potřeba u sekvenčních obvodů sledovat kromě vstupních proměnných ještě jeho vnitřní proměnné – vnitřní stav. Jsou to proměnné, které jsou uchovány v paměťových členech. Existence vnitřních proměnných způsobuje, že stejné hodnoty vstupních proměnných přivedené na vstup obvodu nevyvolávají vždy stejnou odezvu na výstupu obvodu.
Sekvenční obvody dělíme na synchronní a asynchronní.
U asynchronních sekvenčních obvodů se změna vstupní proměnné promítne ihned do stavu sekvenčního obvodu. U synchronních sekvenčních obvodů je zaveden řídicí synchronizační signál (hodinový signál, hodiny). Změna vstupní proměnné se promítne do stavu sekvenčního obvodu až při příchodu hodinového signálu.
Paměťová část sekvenčního obvodu je tvořena kombinačním obvodem, ve kterém byla zavedena zpětná vazba. Tomuto zapojení říkáme bistabilní klopný obvod. Jeho úkolem je převzít informaci přivedenou na vstupu obvodu a uchovat tuto hodnotu, i když vstupní informace již zmizí. Typická paměťová část je klopný obvod RS.
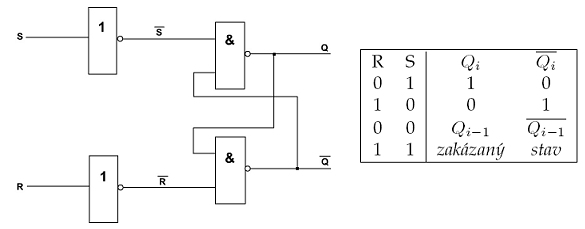
Klopný obvod RS
je jedním z nejjednodušších klopných obvodů. Obvykle se zapojuje ze dvou dvouvstupých hradel NAND. Výstup prvního NANDu vede do jednoho ze vstupů druhého NANDu, výstup druhého NANDu vede do jednoho ze vstupů prvního NANDu.
Vstup R označuje Reset. Přivedení hodnoty logická 1 na tento vstup vynuluje hodnotu Q. Vstup S označuje Set, přivedení hodnoty logická 1 na tento vstup nastaví hodnotu Q na logickou 1. Pokud je na R a zároveň na S logická 1, jde o zakázaný stav.
Pojem zakázaný stav pochází z doby, kdy byl tento obvod realizován dvěma invertory, u kterých nebyl eliminován zpětný přenos přes jednotlivé tranzistory. Současné buzení obou vstupů vedlo k tomu, že se výstupní veličiny dostávaly do zakázaného pásma a tranzistory přecházely ze saturace do aktivní zóny svých charakteristik. Při používání obvyklých dnešních logických členů lze R=S=1 používat jako kterýkoliv jiný stav. Pokud je na R a zároveň na S logická 0, obvod si „pamatuje“ minulý stav výstupů.
Problém nastává při přechodu z R = 0, S = 0 na R = 1 a S = 1. V tomto případě není jasné, do kterého stavu se klopný obvod překlopí (závisí na nesymetrii reálného obvodu).
Stav R = 1, S = 1 lze nazývat nestabilním nebo zakázaným.
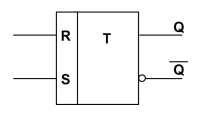
Značka:
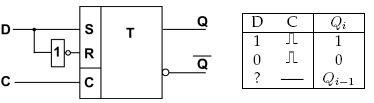
RS může být konstruován pro řízení nulami i jedničkami. Pravdivostní tabulka a schéma zapojení obvyklejšího RS řízeného jedničkami vypadá následovně.
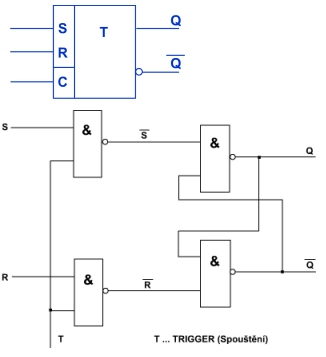
Klopný obvod RS se synchronizací je používán jako základ dalších obvodů. Změna stavu je do obvodu propagována pouze je-li hodinovým kmitočtem na vývod T přiveden patřičný impuls. Obvody mohou být řízeny hladinami (0,1) a hranami (sestupná vzestupná) hodinového kmitočtu.
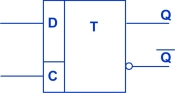
Klopný obvod D
Vznikne doplněním obvodu RS s časovou synchronizací o invertor mezi vstupy. Tím dojde k eliminaci možných stavů na dva. D je vždy řízen synchronizací, obvod se při přivedení hodinového kmitočtu přepne do stavu podle logické úrovně přivedené na vývod D. Vlastně realizuje jednobitovou paměť. Každý hodinový pulz způsobí zapamatování hodnoty vstupu.
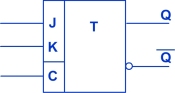
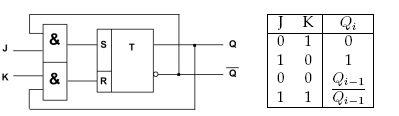
Klopný obvod JK
Vývody mají obdobnou funkci jako u RS, J nastavuje hodnotu logická 1, K nastavuje hodnotu logická 0.
Navíc se eliminuje zakázaný stav, při současné hodnotě 1 na obou vstupech neguje svůj aktuální stav.
Vyrábí se pouze synchronní varianta.
Typické sekvenční obvody
Obvody v číslicové technice a v elektronice vůbec jsou stavěny z malých stavebních kamenů. Tranzistory (nebo jiné součástky) tvoří hradla logických obvodů, ty tvoří klopné obvody, a ty mohou tvořit další složitější obvody, a ty zase další, které později tvoří rozsáhlé zapojení, jako jsou procesory.
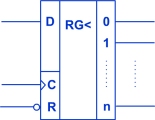
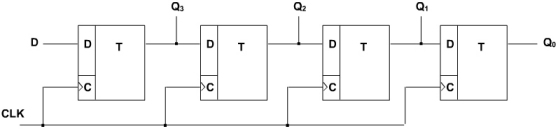
Posuvný registr
Posuvný neboli sériový registr posouvá informaci přivedenou na vstup D postupně po výstupech 0 až n. Jedním taktem signálu CLK se informace posune o jeden klopný obvod.
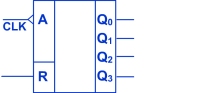
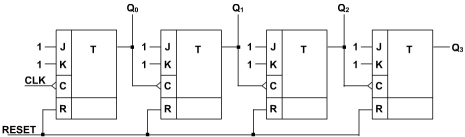
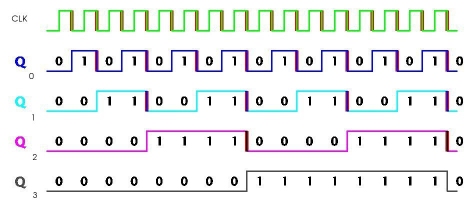
Čítač
Čítač je zařízení, které počítá nebo odpočítává, kolikrát proběhla určitá událost nebo proces. Je synchronizován hodinovým kmitočtem.
Kam dál
Pro lepší pochopení a více příkladu, doporučuji prostudovat na http://www.fi.muni.cz/usr/brandejs/PB151/brandejs_vypocetni_systemy_print.pdf strana 27-37
Použitá literatura
http://www.fi.muni.cz/usr/brandejs/PB151/brandejs_vypocetni_systemy_print.pdf www.kiv.zcu.cz/~netrvalo/vyuka/ppa1-06/cviceni/materialy/PrikladyZobrazeniCisel.pdf
Vypracoval
Petr Kott
petr.kott@post.cz
Otázku si přečetl pan RNDr. Vlastislav Dohnal a rámcově prošel. Jeho podněty pro doplnění textu, opravy nesrovnalostí a odstranění matoucích či k otázce se nevztahujících textů byly do otázky zaneseny. Tato kontrola je jen rámcová, stále se může stát, že v otázce zůstala zapomenutá chybka či nesrovnalost, vyučující za toto nenese odpovědnost, berte tuto rámcovou kontrolu jako formu pomoci od vyučujících pro studenty.