Obsah
N-AP 17
Zadání
Masivně paralelní systémy, paralelní algoritmy, „jemný‟ paralelismus.
Masivně paralelní systémy (MPP)
- alternativa k SMP (symmetric multiprocessing)
- zpravidla pracuje pomocí výměny zpráv
- vhodné např. pro paralelní prohledávání většího množství databází
MPP je systém složený z několika relativně samostatných subsystémů. Jednotlivé procesorové uzly jsou vybaveny vlastní operační pamětí i vlastními vstupně-výstupními kanály a zařízeními. To klade mnohem nižší nároky na datovou propustnost jednotlivých kanálů pro komunikaci mezi jednotlivými procesorovými uzly. U MMP je pak možné zvyšovat počet procesorů až do řádů stovek nebo tisíců a využívají se pro extrémně náročné aplikace. Nevýhodou tohoto systému je vysoká náročnost při vytváření aplikací, které by důkladně využívaly možnosti architektury MMP.
Paralelní algoritmy
- jde o optimalizaci sekvenčního algoritmu
- je třeba zjistit efektivitu paralelizace - tedy rozdíl mezi sekvenčním a paralelním prováděním daného problému
Některé úlohy je prakticky nemožné paralelizovat - např. obsluha I/O, výpočet kryptografické hašovací funkce, nebo výpočet Fibonacciho posloupnosti ( F(n) = F(n-1) + F(n-2) - jednotlivé kroky výpočtu jsou závislé na dvou předchozích hodnotách).
Metodiky návrhu paralelních algoritmů
- task/channel model
- bulk synchronous parallel model
Task/channel model
- výpočet jako množina úloh (tasks) komunikujících pomocí kom. kanálů (channels)
- task - program, lokální paměť, I/O porty
- channel - fronta zpráv spojující výstupní port jednoho tasku se vstupním portem nějakého jiného tasku
- přijímání zpráv je synchronní, blokující
- odesílání zpráv je asynchronní, neblokující
- odlišuje přístup do lokální paměti a komunikaci mezi tasky
- doba běhu paralelního algoritmu je definována jako čas, po který byl aktivní alespoň jeden task.
Fáze návrhu
- partitioning - (rovněž dekompozice), rozdělení úlohy na malé kousky, co nejjemněji
- communication - jak spolu musí jednotlivé podúlohy komunikovat
- agglomeration - slučování podúloh do větších za účelem redukce komunikace (počtu kanálů)
- mapping - jednotlivé tasky přidělujeme procesorům/výpočetním jednotkám
Techniky dekompozice
- rekurzivní dekompozice - vhodné při „rozděl a panuj“, např. quicksort
- datová dekompozice - při velkém množství dat, přidělení částí dat k taskům. Podle:
- vstupních dat
- výstupních dat
- podle vstupních i výstupních dat
- podle mezivýsledků
- dekompozice při prohledávání - při prohledávání stavového stromu (umělá inteligence)
- spekulativní dekompozice - výpočet jednotlivých větví dopředu,pak použití výsledku větve, která byla provedena
- hybridní dekompozice - kombinace
Charakteristika prvotních tasků
- způsob generování prvotních tasků - staticky/dynamicky
- velikost prvotních tasků - čas potřebný pro realizaci, uniformní/neuniformní
- znalost velikosti prvotních tasků
- velikost dat spojených s taskem - poměr vstupních, výstupních dat a náročnost výpočtu
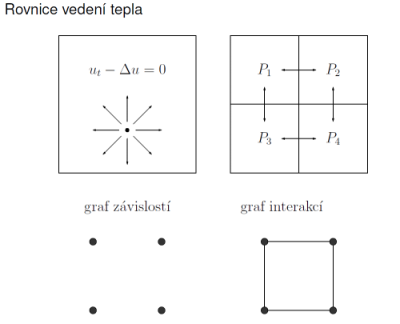
Graf závislosti tasků
- orientovaný acyklický graf
- uzly odpovídají jednotlivým prvotním taskům
- uzly mohou být ohodnoceny podle množství výpočtů, jež je nutné provést k úplnému vyřešení tasku
- task může být řešen, až když jsou vyřešeny všechny podproblémy, ze kterých do něj vede hrana
- graf nemusí být souvislý
- dokonce může být úplně bez hran
Graf interakcí tasků
- vrcholy jsou tasky
- mezi dvěma vrcholy vede hrana, právě když spolu tyto dva tasky musí komunikovat
- graf závislostí je často podgrafem grafu interakcí
Analýza paralelních algoritmů
- použití dvou procesorů místo jednoho prakticky nikdy nevede k ukončení výpočtu v polovičním čase
- paralelizace s sebou vždy nese režii navíc:
- interakce a komunikace mezi jednotlivými procesy
- prostoje procesorů
- nerovnoměrné rozdělení práce
- čekání na ostatní procesy
- některé výpočty navíc oproti sekvenčnímu algoritmu
Amdhalův zákon
Buď část výpočtů, které musí být prováděny čistě sekvenčně. Maximální urychlení
dosažitelné při použití p procesorů je:
- Amdahlův zákon je založen na předpokladu, že se snažíme vyřešit problém dané velikosti, jak nejrychleji to jde
- výpočet nemůžeme nikdy urychlit více než 1/f krát.
Gustavsonův-Barsiho zákon
- vychází z paralelního výpočtu a vyvozuje, kolikrát déle by trval tento výpočet bez paralelizace
- u většiny paralelizovatelných úloh s rostoucí velikostí úlohy roste velikost čistě sekvenční části řádově pomaleji, než celková velikost
- pro p - počet použitých procesorů, s - část z celkového času výpočtu potřebná ke zpracování čistě sériové části, platí:
Příklad: Výpočet běžící na 64 procesorech trvá 220 sekund.
Měření ukazuje, že 5% z celého času výpočtu zabere čistě
sekvenční část algoritmu. Jakého urychlení bylo dosaženo?
„Jemný‟ paralelismus
Používají se u systémů se sdílenou pamětí. Vlákna běží v rámci jedné úlohy, tj. sdílí její kontext. Jednotlivé úlohy sú na seba previazané, a výsledok jedného podproblému závisí od výsledkov iných podproblémov. (problémy vhodné pre superpočítače, počítačový klaster alebo velmi tesne viazané PC klastre s rýchlou sieťou).
Rozdíl mezi jemným a hrubým paralelismem spočívá v poměru doby komunikace mezi uzly a vlastního výpočtu - jemný paralelismus znamená, že ke komunikaci dochází relativně často.
Instrukční paralelismus
- superskalární procesory (pipelining)
- VLIW
Datový paralelismus
- vektorové počítače (CRAY)
- SIMD (Single instruction multiple data)
- grafické karty