2. Kryptografické algoritmy

Principy základních symetrických blokových algoritmů (Feistelovy šifry, DES, AES) a asymetrických algoritmů (RSA, Diffie-Hellman, DSA/ElGamal). Principy konstrukce hašovacích funkcí. Kryptosystémy založené na principu eliptických křivek.

Vypracování

Kerckhoffsův princip

Bezpečnost kryptosystému by měla záviset pouze na utajení klíče, nikoli algoritmu. Algoritmus byl měl být všem znám a všemi ověřitelný, že je bezpečný.

Principy základních symetrických blokových algoritmů (Feistelovy šifry, DES, AES)

Symetrické blokové algoritmy používají tajný klíč sdílený mezi komunikujícími stranami, pracují s bloky dat stanovené délky, na kterou se data musejí zarovnat pomocí paddingu.

Blokové šifry typicky pracují na principu „confusion and diffusion“.

Confusion – statistické závislosti mezi plaintextem a ciphertextem musejí být co nejvíce komplexní, to zajišťují tzv. S-boxy.
Diffusion – každý znak změněný v plaintextu změní celý ciphertext využitím permutací, tzv. P-boxů.

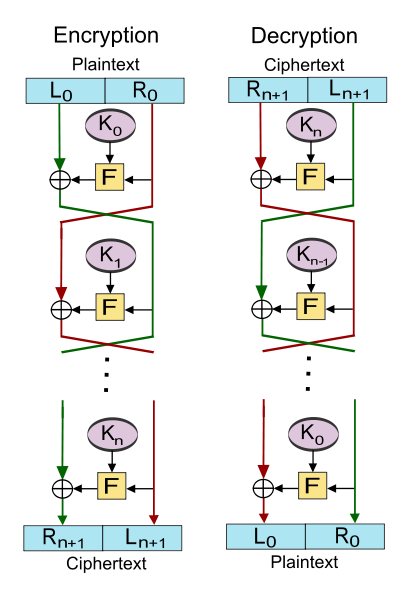
Feistelovy šifry

Šifry, které jsou navrženy jako Feistelova síť.

Tento přístup umožňuje problém návrhu dobré šifry rozdělit na dva podproblémy:

Algoritmus, který určí klíč pro každé kolo.
Funkce $F$ aplikovaná v každém kole.

Výhodou je, že šifrování i dešifrování je prakticky stejné. Funkce $F$ nemusí být invertibilní, stačí pouze otočit pořadí subklíčů.

V každém kole se pracuje pouze s polovinou vstupu. Feistelovy šifry tedy předpokládají vstup sudé délky, který je rozdělen na poloviny – $(L_0, R_0)$ .

$L_{i+1} = R_i$
$R_{i+1} = L_i \oplus F(R_i, K_i)$

Následkem toho mají Feistelovy šifry většinou více kol než jiné algoritmy. Ale v jednotlivých kolech jsou opakovány poměrně jednoduché operace. Pro každé kolo je odvozen čerstvý subklíč z klíče.

Zástupci jsou např. Lucifer, DES, Blowfish, Twofish, CAST-128 a další.

Feistelovy šifry je možné zobecnit tak, že šifra pracuje s nestejně velkými částmi vstupu místo polovin. Také je možné vytvořit nehomogenní Feistelovu síť, kde funkce $F$ není ve všech kolech stejná.

Zdroje

http://en.wikipedia.org/wiki/Feistel_cipher http://cs.wikipedia.org/wiki/Feistelova_%C5%A1ifra.

DES

Data Encryption Standard

Horst Feistel z IBM navrhnul šifru Lucifer, která se po drobných změnách provedených NSA stala FIPS standardem pod názvem DES v roce 1977.

DES má definovanou délku bloku 64 bitů. Délka klíče je 64 bitů (56 bitů bez parity), původní Lucifer pracoval se 128bitovým klíčem.

Feistelova šifra s 16 koly.

Obsahuje iniciální a finální permutace, které po zveřejnění nepřidávají žádnou bezpečnost.

Algoritmus generování subklíčů

Klíč je rozdělen na poloviny (28 bitů dlouhé). V každém kole je zvoleno prvních 24 bitů z každé poloviny a použito jako subklíč (délka 48 bitů). Obě poloviny jsou mezi koly rotovány o jeden nebo dva bity doleva v závislosti na kole.

Funkce F pro každé kolo

Pracuje vždy s polovinou vstupu (32 bitů). Vstup funkce $F$ je rozšířen na 48 bitů. Provede se XOR se subklíčem pro dané kolo. Výsledek projde přes S-boxy, kde se každých 6 bitů nahradí 4 bity podle tabulky (nelineární substituce). Nakonec v každém kole jsou data přeskládána podle dané permutace, P-box.

Pro dnešní použití je klíčový prostor $2^{56}$ příliš malý, také velikost bloku není dostatečná.

Nejpraktičtější známý útok je útok hrubou silou. DES šifra je odolná vůči diferenciální kryptoanalýze. Pro prolomení všech 16 kol je potřeba $2^{49}$ zvolených plaintextů. Při použití lineární kryptoanalýzy je potřeba $2^{43}$ známých plaintextů.

Změny provedené NSA se týkaly použitých S-boxů, jejichž kriteria návrhu nebyly zveřejněny. Tyto změny vedly ke spekulacím, že NSA přidala backdoor. Po zveřejnění vyšlo najevo, že takto upravené S-boxy zvýšily bezpečnost DES.

Triple DES

3DES je varianta DES, která používá klíče větší délky.

Délka bloku je původních 64 bitů. Délka klíče může být 56, 112 a 168 bitů.

$ciphertext = E_{K_3}(D_{K_2}(E_{K_1}(plaintext)))$ $plaintext = D_{K_1}(E_{K_2}(D_{K_3}(ciphertext)))$

Pro 56b klíč $K_1 = K_2 = K_3$ a 3DES je stejný jako DES. Pouze z důvodu zpětné kompatibility.
Pro 112b klíč $K_1 = K_3$ .

112b klíč odpovídá asi 80b bezpečnosti kvůli útokům se známým plaintextem, případně se zvoleným plaintextem.
168b klíč odpovídá 112b bezpečnosti kvůli meet-in-the-middle útoku.

Zdroje

http://en.wikipedia.org/wiki/Data_Encryption_Standard http://en.wikipedia.org/wiki/Triple_DES

AES

Advanced Encryption Standard

NIST vypsal soutěž o novou symetrickou blokovou šifru, která by nahradila DES. Podmínky byly délka bloku 128 bitů, podporované délky klíče 128, 192 a 256 bitů a nová šifra měla být zároveň výkonnější než DES. Z 15 přihlášených vzešlo 5 finalistů: Rijndael, Serpent, Twofish, RC6 a MARS. V roce 2001 byla vítězem vyhlášena šifra Rijndael.

Původní Rijndael mohl pracovat s libovolnou délkou bloku, která byla násobek 32. V AES je délka bloku fixována na 128 bitů.

AES není Feistelova šifra, ale je to tzv. substitution permutation network, tedy také využívá S-boxy a P-boxy. Počet kol závisí na použité délce klíče.

Délka klíče	Počet kol	Označení
128 bitů	9+1	AES-128
192 bitů	11+1	AES-192
256 bitů	13+1	AES-256

V každém kole se provede:

nelineární substituce bytů,
posunutí řádků matice,
promíchání sloupců matice (neprovádí se v posledním kole),
XOR se subklíčem pro dané kolo.

Na rozdíl od DES pro šifrování a dešifrování AES jsou potřeba různé obvody.

Známé útoky

Side-channel útoky na některé implementace, např. OpenSSL.

Nejlepší známé útoky na vlastní šifru jsou pro 7 kol AES-128, 8 kol AES-192 a 9 kol AES-256.

Zdroje

http://en.wikipedia.org/wiki/Advanced_Encryption_Standard

Principy asymetrických algoritmů (RSA, Diffie-Hellman, DSA/ElGamal)

Při použití asymetrických algoritmů má každá strana vlastní klíčový pár skládající se z veřejného a soukromého klíče. Pro zajištění stejné úrovně bezpečnosti jsou potřeba výrazně delší klíče než u symetrických algoritmů.

Výhodou těchto algoritmů je, že odpadá nutnost ustavit sdílený klíč mezi komunikujícími stranami. Na druhou stranu je nějakým způsobem nutné věrohodně propojit veřejný klíč a identitu jeho majitele. PGP využívá tzv. „web of trust“, certifikáty vydané ověřenými certifikačními autoritami, atd.

RSA

Autoři Ron Rivest, Adi Shamir a Leonard Adleman, 1977.

Podobný systém byl vyvinut britskou tajnou službou v roce 1973.

Použití tohoto algoritmu je možné rozdělit do několika fází

Generování klíčového páru
Šifrování
Dešifrování

Generování klíčového páru

výběr 2 prvočísel $p$ a $q$ podobné bitové délky
$n = p \cdot q$ , délka $n$ v bitech je délka klíče
$\varphi (n) = (p-1)(q-1)$ , $\varphi (n)$ je Eulerova funkce
vyber číslo $e : 1 < e < \varphi (n)$ a $\gcd(e,\varphi (n)) = 1$ , dvojce $(n,e)$ je veřejný klíč
$d = e^{-1} \mod \varphi (n)$ , dvojce $(n,d)$ je soukromý klíč

Šifrování

$c \equiv m^e \mod n$ a $0 \le m < n$

Před šifrováním zprávy je zpráva doplněna paddingem, který zajistí, že plaintext nepatří mezi tzv. „insecure plaintexts“. Používal se padding definovaný v PKCS#1, ale bylo ukázáno, že pro některé zprávy tento padding neposkytuje dostatečnou úroveň bezpečnosti. Do PKCS#1 byla přidána definice nového schématu OAEP.

Dešifrování

$m \equiv c^d \mod n$

Kromě šifrování je možné RSA algoritmus použít i pro digitální podpis.

$sig = h(m)^d \mod n$ vytvoří digitální podpis, $h(m)$ značí hash zprávy $m$ .
$hash = sig^e \mod n$ , pokud $hash = h(m)$ , podpis je úspěšně ověřen.

Stejný klíč by neměl být použit pro šifrování a podepisování zpráv zároveň. Výpočty lze urychlit využitím čínské věty o zbytku (CRT).

Bezpečnost

RSA je považován za bezpečný algoritmus, protože není známý způsob, jak efektivně faktorizovat velká čísla. Není známý žádný polynomiální algoritmus.

Shorův algoritmus umožňuje faktorizovat čísla v polynomiálním čase na kvantovém počítači, tedy existence kvantového počítače by znamenala rozbití RSA.

Bezpečnost RSA závisí na volbě prvočísel $p$ a $q$ a do jisté míry i volba $e$ . Malé hodnoty $e$ a špatně implementovaný nebo žádný padding zvyšují riziko útoku. Často $e = 65537$ , to je považováno za kompromis mezi předcházením těchto útoků a efektivitou šifrovacích operací (pro velká $e$ jsou výpočty složitější). Také je důležitá volba soukromého klíče $d$ . Pokud je $d$ dostatečně malé, pak je možné jej efektivně spočítat z $n$ a $e$ .

Timing attack

Při znalosti specifikace HW a době trvání operací je možné odvodit hodnotu soukromého klíče $d$ .

Jako obrana před tímto útokem se místo $c^d \mod n$ počítá $r^e \cdot c^d \mod n$ . $r^e$ je potom možné odstranit. Pro každý ciphertext je použita nová náhodná hodnota $r$ . Této metodě se říká „cryptographic blinding“.

Zdroje

http://en.wikipedia.org/wiki/RSA_(algorithm)

Diffie-Hellman

Algoritmus pro ustavení sdíleného klíče mezi dvěma stranami na nezabezpečeném kanálu bez žádné předchozí sdílené znalosti.

Autoři Whitfield Diffie a Martin Hellman, 1976. Podobný algoritmus byl opět o něco dříve vyvinut britskou tajnou službou.

Alice zvolí $p, g, a$ .
Alice pošle $p, g$ Bobovi.
Bob zvolí $b$ .
Alice spočítá $A = g^a \mod p$ a pošle $A$ Bobovi.
Bob spočítá $B = g^b \mod p$ a pošle $B$ Alici.
Alice spočítá $K = B^a \mod p$ .
Bob spočítá $K = A^b \mod p$ .
Obě strany nyní sdílejí $K = (g^a)^b \mod p = (g^b)^a \mod p$ .

Běžně používaná hodnota $g$ je 2, 3 nebo 5. Čísla $a$ a $b$ a prvočíslo $p$ musejí být velká.

Diffie-Hellman využívá problém diskrétního logaritmu.

Algoritmus ve své původní podobě nezahrnuje autentizaci stran, je tedy možný man-in-the-middle útok.

Toto schéma je možné rozšířit i pro libovolný počet stran. Tyto strany pak sdílejí jeden tajný klíč $g^{x_1 \cdots x_n} \mod p$ , kde $x_1, \ldots, x_n$ jsou tajné exponenty všech zůčastněných stran.

Zdroje

http://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange

DSA

Digital Signature Algorithm, FIPS standard pro digitální podpisy z roku 1991.

Generování klíče

Zvol kryptografickou hashovací funkci $H$ , například SHA-1 nebo SHA-2.
Zvol délku klíče $L$ a $N$ , například 2048 nebo 3072. Doporučené hodnoty pro $(L, N)$ jsou (1024, 160), (2048, 224), (2048, 256) a (3072, 256). $N$ musí být menší nebo rovno délce výstupu hashovací funkce.
Zvol $N$ -bitové prvočíslo $q$ .
Zvol $L$ -bitové prvočíslo $p$ (modulus) takové, že $p - 1$ je násobek $q$ .
Zvol číslo $g$ , jehož stupeň modulo $p$ je $q$ , tedy $g^q \equiv 1 \mod p$ , například $g = h^{\frac{p - 1}{q}}$ mod $p$ pro volitené $h$ ( $1 < h < p - 1$ ). Je nutno zvolit jiné $h$ pokud je výsledek $1$ .
Zvol náhodné $x$ , $0 < x < q$ .
$y = g^x \mod p$

Veřejný klíč je $(p, q, g, y)$ . Soukromý klíč je $x$ .

Podepisování

Zvol (pro zprávu) náhodné $k$ , $0 < k < q$ .
$r = (g^k \mod p) \mod q$
Pokud je $r = 0$ , zvol jiné $k$ a začni znovu.
$s = (k^{-1} \cdot (H(m) + x \cdot r)) \mod q$
Pokud je $s = 0$ , zvol jiné $k$ a začni znovu.
Podpis je $(r, s)$ .

OVěření podpisu

Odmítni podpis pokud není splněno $0 < r < q$ nebo $0 < s < q$ .
$w = s^{-1} \mod q$
$u_1 = H(m) \cdot w \mod q$
$u_2 = r \cdot w \mod q$
$v = ((g^{u_1} \cdot y^{u_2}) \mod p) \mod q$
Podpis je platný pokud $v = r$ .

Hodnota $k$ je pro DSA kritická. Použití stejného $k$ opakovaně, předvídatelného $k$ nebo prozrazení několika bitů $k$ může vést k rozbití DSA.

Zdroje

http://en.wikipedia.org/wiki/Digital_Signature_Algorithm

ElGamal

Autor je Taher ElGamal, 1984.

Generování klíčů

Popis multiplikativní cyklické grupy $G$ řádu $q$ s generátorem $g$ .
Zvol náhodné $x$ , $1 \le x \le q-1$ .
$h = g^x$
$(h, G, q, g)$ je veřejný klíč.
$x$ je soukromý klíč.

Šifrování

Zvol náhodné $y$ , $0 \le y \le q-1$ .
$s = h^y$
$c_1 = g^y$
$c_2 = m' \cdot s$ , $m'$ je prvek $G$ , který odpovídá zprávě $m$ .
$(c_1, c_2) = (g^y, m' \cdot h^y) = (g^y, m' \cdot (g^x)^y)$ je ciphertext.

Dešifrování

$s = c_1^x$
$m' = c_2 \cdot s^{-1}$ , protože platí $c_2 \cdot s^{-1} = m' \cdot h^y \cdot (g^{x \cdot y})^{-1} = m' \cdot g^{x \cdot y} \cdot g^{-x \cdot y} = m'$ .

ElGamal je většinou využíván v hybridních kryptosystémech, symetrický klíč je zašifrován použitím ElGamal a zpráva samotná je šifrovaná symetrickou šifrou.

Bezpečnost ElGamal je založena na problému diskrétního logaritmu.

Existuje i ElGamal algoritmus pro digitální podpisy, který je podobný DSA.

Zdroje

http://en.wikipedia.org/wiki/ElGamal_encryption

Principy konstrukce hašovacích funkcí

Požadované vlastnosti hashovací funkce:

výstup pevné délky pro libovolný vstup,
malá změna na vstupu vede k velké změně na výstupu („avalanche effect“),
ideálně jednosměrná funkce – z hashe je prakticky nemožné zrekonstruovat původní data,
pro stejný vstup vrátí vždy stejný výstup,
uniformní rozdělení výstupů – každý možný výstup je generován s přibližně stejnou pravděpodobností,
slabá bezkoliznost – pro dané $x$ najít $y$ tak, že $h(x) = h(y)$ ,
silná bezkoliznost – výpočetně je velmi náročné najít $x$ a $y$ takové, že $h(x) = h(y)$ .

Hashovací funkce mohou být vytvořeny ze symetrických blokových šifer například pomocí konstrukcí Miyaguchi-Preneel nebo Matyas-Meyer-Oseas.

Kryptosystémy založené na principu eliptických křivek

Asymetrická kryptografie, která využívá eliptické křivky nad konečnými tělesy.

Eliptické křivky jsou takové, které splňují $y^2=x^3 + ax + b$ a,b racionální nebo integer.
Počítá se modulo n
Pracujeme jen s křivkami, které nemají vícečetné kořeny. (4a^3 + 27b^2 = 0)
2 možné tvary grafů
Lze jednoduše sčítat body na křivce (asi i násobit)
Křivky mají konečně mnoho bodů, které lze generovat z daných bodů pomocí sčítání

Problém diskrétního algoritmu na eliptických křivkách:

hledat k takové, že A.k = B. A,B jsou body na křivce
Není znám takový efektivní algoritmus
Je třeba hledat eliptickou křivku nad velkými poli.

Převod diskrétního alg. klasického na EC diskr. alg.

Plaintext → bod na eliptické křivce
Změnit krypto protokol z modulární multiplikace na sčítání bodů na křivce, exponenciální fce změň na násobení bodů
Spočítej bod, přiřaď cyphertext.

Založeno na problému hledání diskrétního logaritmu náhodné eliptické křivky s ohledem na zvolený bod.

Např. ECDH (Elliptic curve Diffie–Hellman), ECDSA (Elliptic Curve DSA) a další.

Pro zajištění 128bitové bezpečnosti je potřeba křivka nad $F_q$ , kde $q \approx 2^{256}$ . Pro srovnání RSA potřebuje 3072bitové klíče pro dosažení stejné úrovně bezpečnosti.

Materiály

Kapitola o kryptografických standardech, Labak I
PA018 - Cryptography, its application, key management, standards
Něco je ve vypracované 4. otázce oboru PSK

Vypracoval

Ondra Mokoš
Předělané eliptické křivky: Marcel Poul