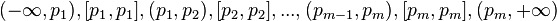Obsah
Zadání
Datové struktury pro prostorové vyhledávání. Vyhledávání podle rozsahů, multidimenzionální binární stromy, stromy úseček.
(Staré znenie:)
Datové struktury pro prostorové vyhledávání. Vyhledávání podle rozsahů, multidimenzionální binární stromy,metoda přímého přístupu, stromy úseček. Sjednocení a průniky obdélníků.
Pozn.: některé matematické základy poskytují poznámky z předmětu Geometrické algoritmy (viz Použité zdroje).
Datové struktury pro prostorové vyhledávání
Příklady elementárních úloh
- Lokalizace bodu v 2-3D prostoru - hledání objektu, kterému patří daný bod
- Hledání nejbližších n bodů od daného středu - globální varianta: hledání nejbližší dvojice bodů
- Zpracování objektů podle vzdálenosti od středu
- Hledání průsečíku na množině úseček (křivek)
- Hledání nejbližšího průsečíku s 3D scénou
- Intervalové dotazy v 2-3D prostoru
- Windowing problém - ořezávání úseček podle předem zadaného polygonálního okna
- Množinové operace nad mapovými objekty - oblasti, linie, bodové objekty
- Testy kolizí a minimálních vzdáleností mezi objekty
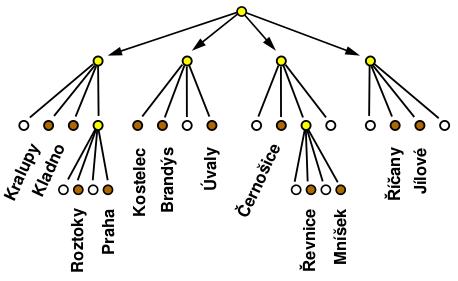
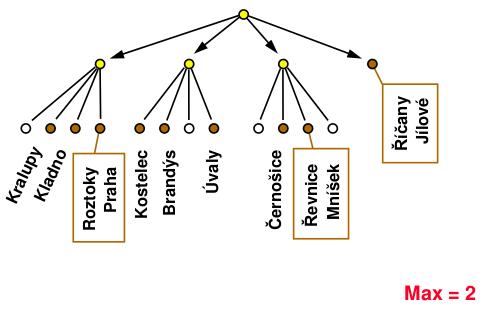
Ortogonální vyhledávání – motivace
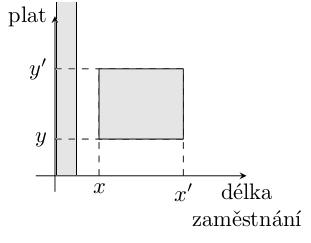
Máme databázi pracovníků firmy, která obsahuje následující údaje pro každého zaměstnance: délku zaměstnání, plat, nemocnost, počet prohřešků. Dva z těchto údajů si můžeme představit jako souřadnice bodů ve dvourozměrném prostoru:
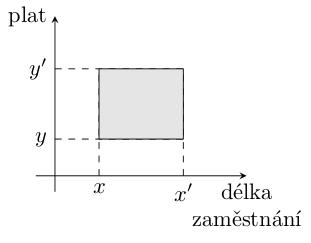 Každý bod představuje jednoho pracovníka. Vyhledávání je dáno obdélníkem [x, x'] * [y, y'].
Každý bod představuje jednoho pracovníka. Vyhledávání je dáno obdélníkem [x, x'] * [y, y'].
Binary Space Partition trees
BSP stromy jsou binární stromy sloužící k prostorovému třídění scény obecně v n rozměrném prostoru . Celá scéna je rekurzivně dělena nadrovinou . Listy BSP stromu odpovídají konvexnímu rozkladu scény. Prostor určený jedním listem obsahuje maximálně jeden objekt (případě zlomek objektu).
 Tvoří se rekurzivně dokud množina objektů obsahuje více než jeden objekt.
Tvoří se rekurzivně dokud množina objektů obsahuje více než jeden objekt.
Dělicí nadroviny mohou být libovolné nebo pouze ortogonální (= snazší zpracování, ale může mít menší schopnost rozdělit scénu = je potřeba více dělení).
Využití
Malířův algoritmus
Malířův algoritmus rekurzivně prochází stromem. Pokud je uzel listem, vykreslí ho, jinak rekurzivně vykresluje větve – nejprve vzdálenější.
Detekce kolizí
Pokud máme BSP strom scény a chceme detekovat kolizi nového tělesa, stačí zjistit, které listy BSP stromu nový objekt protíná a zde otestovat kolizi (s jedním tělesem).
Quad strom
Speciální případ BSP stromu.
Dělí prostorovou scénu pouze v ortogonálních směrech. Rozšířením quad stromu z dvourozměrného do třírozměrného prostoru jsou tzv. oct strom. Informace o objektech uloženy v listech.
Využití
Quad strom s kbelíkem („bucket“)
V jednom listu (uzlu) se ukládají údaje o několika objektech pro zmenšení spotřeby paměti i času přístupu – menší režie na údržbu ukazatelů.
kD (k-dimenzionální) strom
Speciální případ BSP stromu. Více dimenzionální vyvážený binární vyhledávací strom provádějící dělení střídavě podle x-ové a y-ové souřadnice (ve 2D).
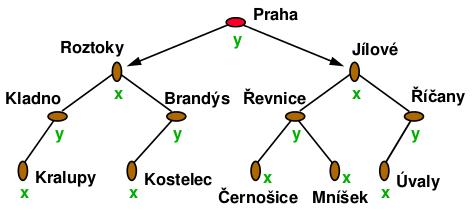 Region odpovídající uzlu v (region(v)) je obdélník, který může být neomezený v jednom nebo více směrech.
Region odpovídající uzlu v (region(v)) je obdélník, který může být neomezený v jednom nebo více směrech.
- Region kořenu kD-stromu je celá rovina
- Bod je uložen v podstromu uzlu v právě tehdy, jestliže leží v regionu region(v).
- Podstrom uzlu v prohledáváme pouze tehdy, jestliže region(v) má neprázdný průnik s dotazovaným obdélníkovým rozsahem.
- Jestliže je region(v) zcela obsažen v dotazovaném rozsahu, můžeme nahlásit všechny body celého podstromu v.
Prohledávání probíhá rekurzivně po větvích – pokud je zkoumaný uzel listem a odpovídá regionu, je nahlášen, jinak se zkoumají větve – pokud je větev celá v rozsahu, je nahlášena, pokud rozsah protíná, je rekurzivně zkoumána.
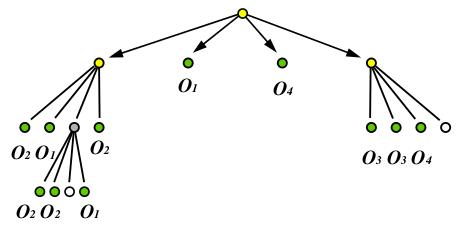
Rozsahový strom (range tree)
Range tree je složen z jednoho binárního vyváženého stromu T, jehož listy jsou body množiny P v rovině seřazené podle x-ové souřadnice. (Předpokládáme, že každé dva body mají různé souřadnice x a y). Uzly stromu jsou ohodnoceny nejvyšším číslem své levé větve. Rozsahový strom pro d-dimenzionální body množiny P je rekurzivně definovaný víceúrovňový binární vyhledávací strom. Každá jeho úroveň je binární vyhledávací strom na jedné z d dimenzí. První úrovní je binární vyhledávací strom na první z d souřadnic. Každý vrchol v tohoto stromu obsahuje asociovanou strukturu, která je d-1 dimenzionálním stromem na posledních d-1 souřadnicích bodu uloženého v podstromu v.
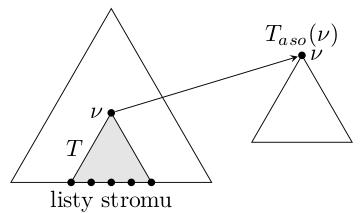 Strom se stejnými listy jako podstrom v T, ale uspořádanými podle souřadnice y.
Strom se stejnými listy jako podstrom v T, ale uspořádanými podle souřadnice y.
Např. pro 3 dimenze:
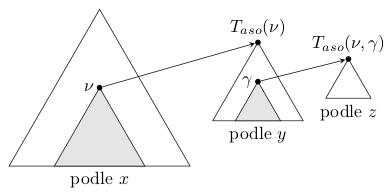 Vyhledávání rozsahů (regionů) probíhá nejprve podle první souřadnice, při nalezení správného rozsahu (který obsahuje list v), pokračuje postupně podle dalších souřadnic, jejichž stromy jsou uloženy asociovaně k uzlu v.
Vyhledávání rozsahů (regionů) probíhá nejprve podle první souřadnice, při nalezení správného rozsahu (který obsahuje list v), pokračuje postupně podle dalších souřadnic, jejichž stromy jsou uloženy asociovaně k uzlu v.
Hledání v datech s indexy
Toto je uvedeno navíc – otázka se na toto neptá, ale tak pro doplnění a rozšíření metody přímého přístupu. Protože jinak tam není moc o čem mluvit…
Tyto metody hledání mohou být aplikovány pouze na soubory dat, ke kterým byly vytvořeny indexové tabulky (viz odstavec o metodách uložení s indexy). Protože indexové tabulky jsou vytvářeny na základě hodnot klíčů, je možno hledat záznam pouze podle kriteria, kterým je hodnota klíče.
Při této metodě se hledání ve vlastním souboru dat převádí na hledání dané hodnoty klíče v indexové tabulce. Po nalezení záznamu indexové tabulky je z pole adresy získána adresa datového záznamu v souboru dat, a tento záznam se pak přímo získá jediným čtením.
Pro hodnocení metod hledání v datech s indexy platí vše, co bylo uvedeno dříve, ovšem aplikováno na soubor indexů. Organizace uložení v souboru indexů tedy určuje efektivitu používání souborů s indexy. Protože z dosud hodnocených metod hledání je nejméně efektivní sekvenční metoda, téměř nikdy se nepoužívá ani sekvenční organizace uložení, ani sekvenční hledání.
Velmi často se pro indexová tabulky používá uložení s odkazy. Záznam pak má 6 polí: čtyři pole s odkazy (na předchůdce, následovníka, a na levého a pravého souseda), jedno pole pro hodnotu klíče a jedno pro hodnotu adresy záznamu. Indexová tabulka pak má tvar stromu (z teorie grafů). Každý záznam je pak jedním uzlem v tomto grafu, hrany grafu jsou obrazem odkazů. Výhodou je možnost ukládat v každém uzlu ne kompletní hodnoty klíče, ale jen část hodnoty klíče náležející dané úrovni uzlu v grafu.
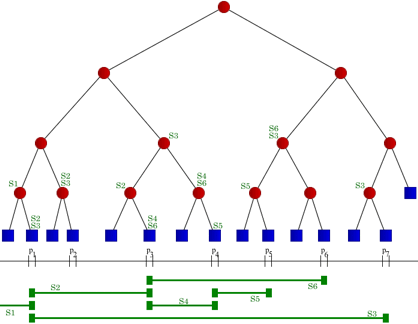
Stromy úseček (Segment trees)
Stromová datová struktura pro uložení intervalů (úseček). Dovoluje dotazování, která úsečka odpovídá specifikovanému bodu. Principiálně statická struktura – obsah nemůže být měněn, pokud byl jednou strom sestaven.
Strom úseček je binární vyhledávací strom sestaveny nad množinou koncových bodů úseček. Koncové body dělí výchozí interval (-∞; ∞) na disjunktní elementární intervaly. Každý list stromu odpovídá jinému elementárnímu intervalu. Vnitřní vrcholy odpovídají sjednocení intervalů svých větví. Vrcholy obsahují pole přiřazených intervalů bez těch, které jsou již přiřazeny v jejich rodičích.
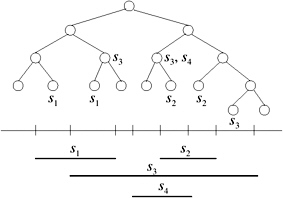 Segmentový strom můžeme dále „vylepšit“, aby mohl obsahovat i body (úsečky nulové délky – intervaly [p; p]) a rozlišovat uzavřené a otevřené intervaly tak, že do množiny intervalů přidáme intervaly [p; p] pro každý bod p množiny koncových bodů:
Segmentový strom můžeme dále „vylepšit“, aby mohl obsahovat i body (úsečky nulové délky – intervaly [p; p]) a rozlišovat uzavřené a otevřené intervaly tak, že do množiny intervalů přidáme intervaly [p; p] pro každý bod p množiny koncových bodů:
Koncept segmentových stromů lze zobecnit i do vyšších dimenzí, na rozdíl např. od intervalových stromů. Intervalové stromy ale mají menší paměťovou náročnost, takže může být vhodné budovat hybridní strom, který je ve vyšších úrovních segmentový a v nižších intervalový.
Sjednocení a průniky obdélníků
Opět není jisté, čeho se týká. Zřejmě jde o sjednocení a průniky obdélníků (= regionů) při vyhledávání ve více-dimenzionálních datech, tedy něco jako vyhledávání v databázi s SQL dotazem WHERE … AND … resp. WHERE … OR … . Ovšem ani k tomu nikde žádné relevantní informace nejsou.
Regiony dotazu v prostorovém vyhledávání jsou obdélníky výsledků. Např. v tomto dotazu:
 jsou výsledkem všichni zaměstnanci, jejichž délka zaměstnání je v rozmezí x – x' a mají plat v rozmezí y – y'. Pokud bychom chtěli vyhledávat s logickou podmínkou or (nebo), obdržíme dva obdélníky, jejichž sjednocením je výsledek dotazu. Např. dotaz na zaměstnance, jejichž délka zaměstnání je v rozmezí x – x' a mají plat v rozmezí y – y' nebo jejichž délka zaměstnání je nejvíce x / 2, dostaneme následující odpověď:
jsou výsledkem všichni zaměstnanci, jejichž délka zaměstnání je v rozmezí x – x' a mají plat v rozmezí y – y'. Pokud bychom chtěli vyhledávat s logickou podmínkou or (nebo), obdržíme dva obdélníky, jejichž sjednocením je výsledek dotazu. Např. dotaz na zaměstnance, jejichž délka zaměstnání je v rozmezí x – x' a mají plat v rozmezí y – y' nebo jejichž délka zaměstnání je nejvíce x / 2, dostaneme následující odpověď:
 Pokud bychom chtěli vyhledávat s logickou podmínkou and (a zároveň), obdržíme dva obdélníky, jejichž průnikem je výsledek dotazu. (Smysluplný příklad ve 2D mě nenapadá, jelikož všechny dotazy na obdélníky s podmínkou and lze snadno přepsat na jeden dotaz. Např.: obdélník [x₁, x₁'] * [y₁, y₁'] and [x₂, x₂'] * [y₂, y₂'] lze přepsat jako [x, x'] * [y, y'], kde x = max(x₁, x₂), x' = min(x₁', x₂'), y = max(y₁, y₂), y' = min(y₁', y₂'))
Pokud bychom chtěli vyhledávat s logickou podmínkou and (a zároveň), obdržíme dva obdélníky, jejichž průnikem je výsledek dotazu. (Smysluplný příklad ve 2D mě nenapadá, jelikož všechny dotazy na obdélníky s podmínkou and lze snadno přepsat na jeden dotaz. Např.: obdélník [x₁, x₁'] * [y₁, y₁'] and [x₂, x₂'] * [y₂, y₂'] lze přepsat jako [x, x'] * [y, y'], kde x = max(x₁, x₂), x' = min(x₁', x₂'), y = max(y₁, y₂), y' = min(y₁', y₂'))
Obě operace lze v uvedených datových strukturách realizovat pomocí nalezení regionů obou poddotazů a jejich sjednocením, resp. průnikem. Vyhledání by mohlo být také optimalizováno, aby neprocházelo dvakrát společné uzly stromů.
Použité zdroje
Josef Pelikán, Jiří Sochor : PB009 - Základy počítačové grafiky, slajdy. 2012. Fakulta informatiky, Masarykova Univerzita. Brno.
http://geologie.vsb.cz/geoinformatika/kap03.htm
http://en.wikipedia.org/wiki/Segment_tree
http://flylib.com/books/en/2.587.1.48/1/
Ril: Geometrické algoritmy (PřF:M7130). 2011. https://is.muni.cz/auth/of/1431/M7130/podzim2011/geometricke_algoritmy.pdf.