Obsah

Zadanie
Vypracovanie

Zadanie

Parametrické plochy. Plochy dané okrajem, Bezierovy plochy, B-spline plochy, NURBS. Plátování, hladké navázání. Implicitní povrchy.

Vypracovanie

Vyjadrenie plochy môže byť podobne ako u krivky len s doplnením ďalšej dimenzie – explicitné, implicitné a parametrické.

Explicitne zadaná plocha je vyjadrená funkciou $z = f(x,y)$ .

Implicitne zadaná plocha je vyjadrená rovnicou $F(x,y,z) = 0$ (podrobnejšie v časti o implicitných plochách).

Parametrickým vyjaderním plochy $Q(u,v)$ je bodová rovnica dvoch parametrov $u$ a $v$ nadobúdajúcich hodnoty z intervalu $<0,1>$ , ktorá je zadaná ako $Q(u,v) = [x(u,v), y(u,v), z(u,v)]$ .

Dotykový vektor (tečný vektor) $\vec{q_{u}}(u,v)$ v smere parametru $u$ k ploche $Q(u,v)$ a dotykový vektor $\vec{q_{v}}(u,v)$ v smere parametru $v$ sú určené vzťahmi
$\vec{q_{u}}(u,v) = \frac{\partial Q(u,v)}{\partial u}) = \left(\frac{\partial x(u,v)}{\partial u}, \frac{\partial y(u,v)}{\partial u}, \frac{\partial z(u,v)}{\partial u}\right)$ ,
$\vec{q_{v}}(u,v) = \frac{\partial Q(u,v)}{\partial v}) = \left(\frac{\partial x(u,v)}{\partial v}, \frac{\partial y(u,v)}{\partial v}, \frac{\partial z(u,v)}{\partial v}\right)$ .

Rovnica dotykovej roviny (tečné roviny) je určené ako $T(r,s) = Q(u,v) + r.\vec{q_{u}} + s.\vec{q_{v}}; r,s \in R$ .
Skruty (skrutové vektory) charakterizujú „vyklenutie“ plochy v miestach napojenia. Sú definované pomocou zmiešaných parciálnych derivácií ako $\vec{q_{uv}}(u,v) = \frac{\partial^{2}Q(u,v)}{\partial u \partial v}$ .
Normálu (kolmicu) k ploche v bode $Q$ určíme ako normalizovaný vektorový súčin dotykových vektorov, teda $\vec{n} = \frac{\vec{q_{u}} \times \vec{q_{v}}}{|\vec{q_{u}} \times \vec{q_{v}}|}$ .

Hlavná krivka plochy v smere parametru $u$ je každá krivka určená rovnicou $Q(u,k)$ pevného parametru $k$ a premenného parametru $u$ . Analogicky to platí aj pre hlavnú krivku v smere parametru $v$ . Rohy plochy sú body $Q(0,0)$ , $Q(1,0)$ , $Q(0,1)$ a $Q(1,1)$ . Strany plochy $Q(u,v)$ sú hlavné krivky v oboch smeroch, kde pevný parameter má hodnotu $0$ alebo $1$ . Všetky strany dohromady tvoria okraj plochy.

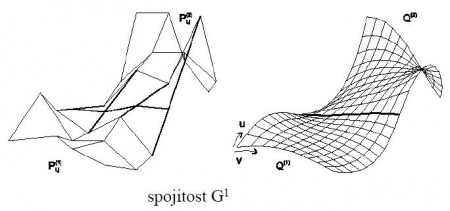
Analógiou naväzovania segmentov a ich skladania do krivky aj plochy sa skladajú z častí, ktoré voláme pláty. Naväzovanie plôch sa nazýva plátovanie. AJ pri plochách rozoznávame parametrickú spojitosť $C$ a gemometrickú spojitosť $G$ . Napríklad dva pláty sú $C^{1}$ spojité, ak majú spoločnú stranu a priečne parciálne derivácie vo všetkých bodoch spoločnej strany sú zhodné.

Plochy sa zadávajú riadiacimi bodmi a bázovými funkciami. Väčšinou sa používajú plochy aproximačné. Interpolácia vo viac ako dvoch dimenziách je náročná a vyžaduje rozsiahle výpočty. Interpolačná plocha $P_{ij}$ má $(m + 1) \times (n + 1)$ bodov. Interpoláciou vektorovým polynómom je možné plochu zapísať ako $\vec{P}(u,v) = \sum_{i=0}^{m} \sum_{j=0}^{n} b_{ij}.u^{i}.v^{j}$ .

Na aproximačné vyjadrenie plôch sa používajú tzv. 12-vektorový Hermitovský plát alebo 16-vektorový (obsahuje navyše 4 skrutové vektory v každom rohu plátu).

Plochy zadané okrajom

Plochy môžu byť zadané aj pomocou všetkých kriviek určujúcich okraj, napr. 4 v prípade štvoruholníkového plátu.

Bilineárna Coonsova plocha je jednoznačne určená štyrmi krivkami $P(u,0)$ , $P(u,1)$ , $P(0,v)$ a $P(1,v)$ , ktoré musia tvoriť uzavretý okraj budúceho plátu.
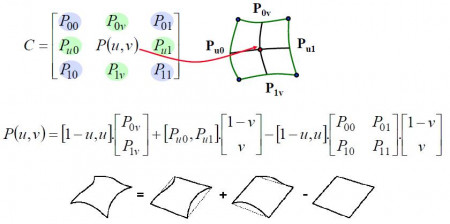
Rovnica, ktorá určuje bilineárnu Coonsovu plochu sa dá zjednodušene zapísať v tvare $[1-u,-1,u].\mathbf{C}.[1-v,-1,v]^{T} = 0$ , kde bod uprostred matice $\mathbf{C}$ je hľadaným riešením tejto implicitnej rovnice. Na výpočet bilineárnej plochy však slúži explicitné vyjadrenie tejto rovnice, ktoré môžeme vidieť na obrázku spolu s grafickým znázornením výpočtu. Zásadným problémom plochy je, že zo zadaného okraja nie je možné jednoducho vyjadriť priečne dotykové vektory a teda nie je ľahké vytvoriť hladké spojenie dvoch takýchto plátov.

Bikubická plocha je rovnako určená štyrmi krivkami, ale popísaná vzťahom $[F_{1}(u),-1,F_{2}(u)].\mathbf{C}.[F_{1}(v),-1,F_{2}(v)]^{T} = 0$ , kde dané funkcie predstavujú Hermitovské polynómy $F_{1}(t) = 2t^{3} - 3t^{2} + 1$ a $F_{2}(t) = -2t^{3} + 3t^{2}$ . Pre rovnaké dôvody ako v predchádzajúcom prípade, ani tieto plochy sa nepoužívajú na plátovanie so spojitou prvou deriváciou.

Až všeobecná bikubická plocha (po česky obecná) umožňuje hladké naväzovanie plátov, keďže je pri nej potrebné zadávať aj dotykové vektory podľa okraja. Okrem 4 spomínaných kriviek ju preto určujú aj priečne vektory pozdĺž okrajov $\vec{p_{v}}(u,0)$ , $\vec{p_{v}}(u,1)$ , $\vec{p_{u}}(0,v)$ a $\vec{p_{u}}(1,v)$ . Ďalej je tiež určená skrutmi v jednotlivých rohoch, teda vektormi $\vec{t}(0,0)$ , $\vec{t}(0,1)$ , $\vec{t}(1,0)$ a $\vec{t}(1,1)$ .
Vzťah pre všeobecnú bikubickú plochu je rozšírený o ďalšie dva Hermitovské polýnómy tretieho stupňa $F_{3}(t) = t^{3} - 2t^{2} + t$ , $F_{4}(t) = t^{3} - t^{2}$ a implicitná rovnica plochy má tvar $[F_{3}(u),F_{1}(u),-1,F_{2}(u),F_{4}(u)].\mathbf{C}.[F_{3}(v),F_{1}(v),-1,F_{2}(v),F_{4}(v)]^{T} = 0$ .

Bézierove plochy

Bézierove plochy používajú niektoré modelovacie systémy k reprezentácii povrchu telies, pretože sú ľahko diferencovateľné, jednoducho sa modelujú a tiež je pomerne ľahko môžné vypočítať priesečník s lúčom. Tieto plochy sú vlastne špeciálnym prípadom zložitejšej reprezentácie povrchov pomocou NURBS.

Na obrázku vidíme definíciu Bézierovej plochy, kde bázové funkcie $B_{i}^{m}$ a $B_{j}^{n}$ predstavujú Bernsteinove polynómy $m$ -tého (resp. $n$ -tého) stupňa.

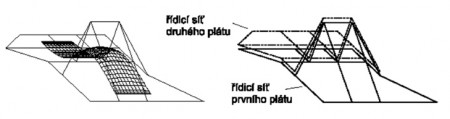
Bézierova plocha pri zmene jedného riadiaceho bodu zmení celý svoj tvar. Táto vlastnosť je nevýhodná, a preto sa plochy plátujú. Pre napojenie plátov so spojitosťou nultého stupňa musíme zabezpečiť stotožnenie riadiacich bodov, ktoré určujú príslušnú stranu. Na obrázku vidíme príklad napojenia s geometrickou spojitosťou prvého stupňa ( $G^{1}$ ), ktorá vzniká vtedy, ak sú priečne dotykové vektory lineárne závislé.

Metódou na zobrazovanie Bézierových plôch je polygonizácia založená na princípe rekurzívneho delenia (patch splitting), pričom sa využíva algoritmus deCasteljau.

B-spline plochy

Pre modelovanie sú B-spline plochy oveľa výhodnejšie, pretože sa naväzujú omnoho jednoduchšie než Hermitovské alebo Bézierove pláty. B-spline plochy $n$ -tého stupňa totiž zaručujú $C^{n-1}$ spojitosť vo všetkých svojich bodoch. ďalšou výhodou je, že zmenou jedného riadiaceho bodu zmeníme vždy iba časť danej plochy.

Medzi vlastnosti B-spline plochy patrí:

celá plocha leží v konvexnej obálke svojich riadiacich bodov,
pri zmene riadiaceho bodu sa zmenia iba pláty, ktoré sú ním určené
plocha síce všeobecne neprechádza krajnými bodmi plochy, je to ale možné dosiahnuť násobnými riadiacimi bodmi
sú invariantné k lineárnym transformáciam (otočenie, posun, zmena mierky, skosenie)

NURBS plochy

Neuniformné racionálne B-spline plochy sú zovšeobecnením B-spline plôch a predstavujú dnes štandard v priemyslovom modelovaní. Umožňujú definovať širokú škálu plôch, napr. voľne tvarovateľné plochy na báze racionálnych polynómov (free form surfaces) alebo plochy založené na priamkách a kuželosečkách. Aj ich vznik datujeme do polovice 20. storočia pre potreby presnej matematickej reprezentácie tvaru karosérie áut, trupu lodí či lietadiel.

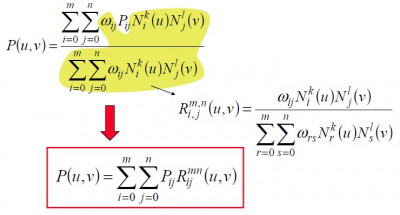
Z definície, $N_{i}^{k}(u)$ a $N_{j}^{l}(v)$ sú normalizované B-spline bázové funkcie ( $k$ , $l$ sú stupne polynómu) a $\omega_{i,j}$ sú váhy jednotlivých bodov (homogénne súradnice) riadiace siete $\mathbf{P}$ . Váhy podobe ako v prípade kriviek určujú vplyv riadiaceho bodu na plochu, pričom so zvyšujúcou sa hodnotou váhy sa plocha k bodu primkýna. Podobne ako Bézierove plochy, aj NURBS sú invariantné k lineárnym transformáciam a vďaka racionalite sú naviac invariantné aj k perspektívnej projekcii.

O plochách NURBS hovoríme aj v prípade modelovacej techniky zvanej šablónovanie (sweeping), kde patria napríklad:

translačné šablónovanie - obrys je ľubovoľný a trajektória, po ktorej je obrys ťahaný je úsečka, dostávame tzv. priamkové plochy popísané vzťahom $Q(u,v) = (1-u).P(0,v) + u.P(1,v)$ , typy translačného šablónovania sú – po úsečke s nemeniacou sa profilovou krivkou (extruded surface), po úsečke medzi danými profilmi (ruled surface) a poťahovanie (skinning),
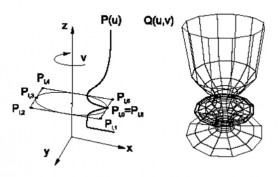
rotačné šablónovanie - obrys je ľubovoľný a trajektória, po ktorej je obrys ťahaný je kružnica alebo jej časť – toto teleso je možné získať aj rotáciou okolo osi, výsledkom je rotačná plocha (viď obrázok),
všeobecné šablónovanie - obrys i trajektória je ľubovoľná, získavame zovšeobecnenú valcovú plochu.

Implicitné povrchy

Implicitné vyjadrenie plochy tvorí alternatívu k povrchu definovanom pomocou polygónov alebo parametrických plátov. Výhodou je napríklad kompaktnejšia reprezentácia či jednoduchšie sledovanie lúča (paprsku). Výpočet sledovania lúča je ale časovo náročný, rovnako je náročné aj zobrazovanie plochy v reálnom čase. Väčšina zobrazovacích metód v konečom dôsledku aj tak prevádza implicitné plochy na parametrické vyjadrenie alebo rovinné plošky, tzv. polygonizácia implicitných plôch.

Funkcia $f(x,y,z)$ priraďuje každému bodu v priestore nejakú skalárnu hodnotu a definuje teda skalárne pole. Nami hľadaný objekt je izoplocha, teda množina bodov s rovnakou funkčnou hodnotou. Ak $f = 0$ , bod leží na povrchu plochy. Ak $f < 0$ alebo $f > 0$ , možeme hovoriť, že bod leží vo vnútri (alebo vonku) objektu ohraničeného plochou, no ktorá hodnota označuje čo, už závisí na konkrétnom kontexte.

Normály povrchu sú obvykle určené gradientom príslušnej funkcie, teda $\nabla f(x,y,z) = \left(\frac{df}{dx}, \frac{df}{dy}, \frac{df}{dz}\right)$ .

Medzi implicitné povrchy zaraďujeme blobby objekty (kvapky) od J. Blinna, metaballs či soft objects od Wyvilla.

Príkladom implicitnej plochy (množiny bodov $P$ v trojrozmernom priestore) je guľová plocha zadaná implicitnou rovnicou $Q(P) = x^{2} + y^{2} + z^{2} = r^{2}$ .

Implicitné plochy môžu byť reprezentované aj takzvanými dištančnými povrchmi (viď zoznam na obrázku).

Delené povrchy (nie je súčasťou novej otázky)

Modely sú reprezentované pomocou mnohouholníkov, avšak len málokedy majú objekty reálneho sveta ostré hrany. Pri modelovaní pomocou polygónov nastávajú problémy s úrovňou detailov. Aj keď model aproximujeme dostatočným množstvom polygónov, pri zväčšení sa problém hrán znovu objaví. Riešením je delenie povrchov.

Polygonálna sieť je množina vrcholov a prepojení medzi nimi, čím definuje topológiu povrchu a vymedzuje jednotlivé plošky. Delenie je rekurzívny proces, pri ktorom je polygónová sieť zjemňovaná pridávaním vrcholov a plošiek. Pri zvyšovaní počtu vrcholov síce dochádza k výraznému spomaleniu a takéto modely sú pamäťovo náročné, ale aj napriek tomu je zjemňovanie siete významné pri tvorbe animácií a statických modelov. Generované povrchy, kedy zvyšujeme úroveň detailov sa nazývajú delené povrchy (subdivision surfaces).

Povrchy môžeme deliť nad poškami alebo deliť nad vrcholmi. Dôležitým faktorom pri delení povrchov je topológia polygónovej siete. Môže sa jednať napríklad o trojuholníkovú sieť, štvorcovú sieť alebo sieť s ľubovoľnou topológiou. Obidve nasledujúce prezentované deliace schémy však dokážu deliť povrchy s ľubovoľnou topológiou, čo je ich veľká výhoda.

Doo-Sabin

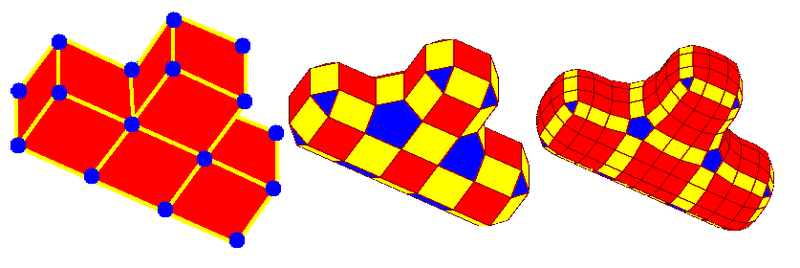
Doo-Sabin je aproximačná deliaca schéma používajúca delenie nad vrcholmi.

Ploškový bod je vypočítaný ako priemer všetkých vrcholov plošky podľa vzťahu $V_{F} = \frac{1}{N} \sum_{i=1}^{N} V_{i}$ . Pre každý vrchol potom vypočítame nový vrchol prislúchajúci k pôvodnému ako priemer ploškového bodu, pôvodného vrcholu a stredu hrán, ktoré z neho vychádzajú, teda $V' = \frac{V + V_{F} + M_{E1} + M_{E2}}{4}$ . Takto vznikajú 3 typy nových plošiek – plošková (červená), hranová (žltá) a vrcholová (modrá).

Povrchy generované delením Doo-Sabin spĺňajú podmienku $C^{1}$ spojitosti (okrem hranice, kde je sieť otvorená).

Catmull-Clark

(Tu môžete spomenúť, docent Sochor to má rád , oskarový krátkometrážny animovaný film od štúdia Pixar „Geriho hra (1997)“, ktorý režíroval český rodák Jan Pinkava a pri jeho tvorbe bola naplno využitá práve deliaca schéma Catmull-Clark (viac informácií v článku http://graphics.pixar.com/library/Geri/paper.pdf).)

Catmull-Clark je aproximačná deliaca schéma používajúca delenie nad ploškami.

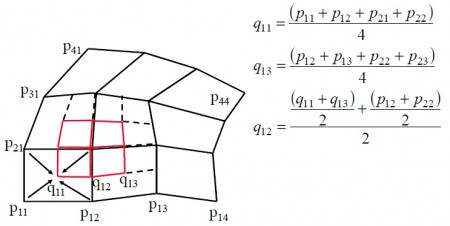
Podobne ako pri delení Doo-Sabin, aj tu si spočítame poškový bod $V_{F}$ , avšak zatiaľ čo v predchádzajúcom prípade plnil len funkciu medzivýsledku pri výpočte nových bodov, teraz sa stáva súčasťou výslednej zjemnenej siete. Ďalej určíme hranový bod $V_{E}$ ako priemer vrcholov hrany a ploškových bodov podľa vzťahu $V_{E} = \frac{E_{1} + E_{2} + V_{F1} + V_{F2}}{4}$ . Posledný typ bodu, ktorý musíme spočítať je vrcholový bod $V_{V}$ zjednodušene vyjadrený vzťahom $V_{V} = \frac{Q + 2R + S.(n-3)}{n}$ , kde $Q$ je priemer nových stenových bodov na stenách priľahlých k vrcholu, $R$ je priemer nových hranových bodov a $S$ je pôvodný vrchol.

Povrchy generované delením Catmull-Clark spĺňajú podmienku $C^{1}$ spojitosti (mimo výnimočné vrcholy dokonca až spojitosť $C^{2}$ ).