Obsah
Zadání
Modelování v počítačové grafice. Druhy modelů, vytváření a modifikace, zobrazení. Lokální a globální úpravy modelů, deformační metody FFD. (PA010, PB009, PA157, PA158)
Druhy modelů
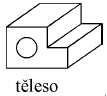
Těleso je množina bodů v 3D splňující určitá kritéria (např. sousednost).
Trojúhelníková síť
Trojúhelníková síť (triangle mesh) je množina trojúhelníků sdílející své hrany.
- jednoduchá, vždy konvexní, každý vrchol leží v rovině
- pro vyplňování existují velmi rychlé algoritmy
- zobrazování je podporováno grafickým procesorem
- výpočty lze snadno optimalizovat (např. sledování paprsků)
- Datová struktura: geometrická část (obsahuje souřadnice vrcholů) + topologická část (které vrcholy tvoří trojúhelník, které trojúhelníky spolu sousedí)
Není vhodná na modelování tvaru těles a ploch (namísto např. NURBS), ale užitečná při deformaci.
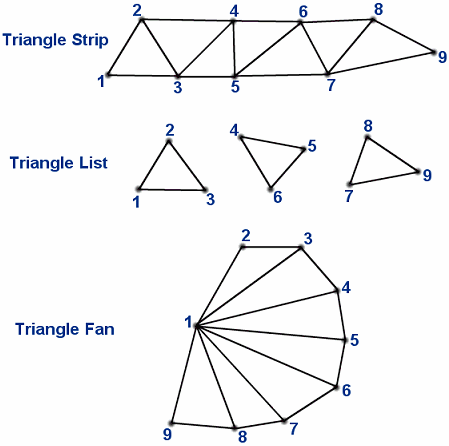
Optimalizace sítě – trojúhelníky pokrývají plochu pravidelně vs. jemněji v místech s větší křivostí. Při zpracování dat v grafickém procesoru je vhodnější popsat síť trojúhelníků pomocí lineární struktury, která zajistí, že každý trojúhelník je zpracován právě jednou: pruh trojúhelníků (triangle strip), vejíř trojúhelníků (triangle fan).
Nevýhody: nesnadné mapování textur, může vzniknout geometrický alias (např. při změně měřítka - crack, u T-vrcholů).
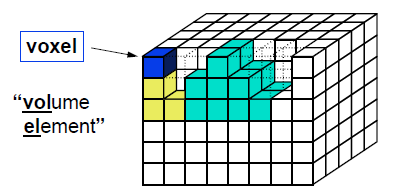
Voxelový model
- pole k x l x m voxelů („volume element“)
- jednobitová varianta (0 – nic, 1 – těleso) vs. vícebitová varianta (0 – nic, n>0 – těleso č. n)
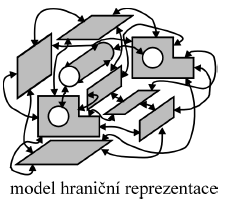
Hraniční reprezentace těles
- popis množiny hraničních bodů
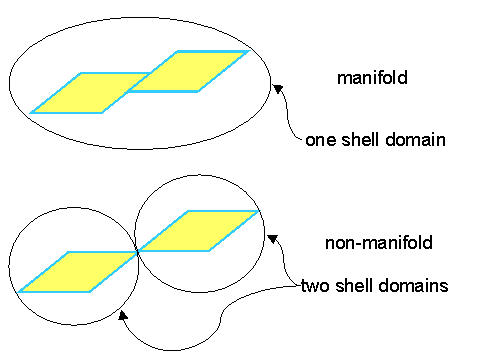
Manifold je těleso, které odpovídá nějakému skutečnému tělesu (tj. jehož hrany incidují právě s 2 plochami, jehož hrany neprotínají jiné plochy, osamocený vrchol nespojuje 2 části tělesa).
Eulerova rovnost
Hraniční reprezentace jednoduchého mnohostěnu splňuje rovnici (opačně nemusí platit, tj. objekt splňující rovnici nemusí být jednoduchým mnohostěnem):
F + V = E + 2
F (faces) – počet ploch
V (vertices) – počet vrcholů
E (edges) – počet hran
Musí platit, že každá hrana propojuje 2 vrcholy, stěny a hrany se neprotínají.
Pro manifoldy s otvory platí zobecněná Eulerova rovnost:
F + V = E + 2 (C – H) + R
R (ring) – počet vnitřních smyček hran
C (component) – počet samostatných komponent tělesa
H (hole) – počet otvorů
Platnost Eulerova rovnosti souvisí s vlastnostmi planárních grafů.
Hranová reprezentace
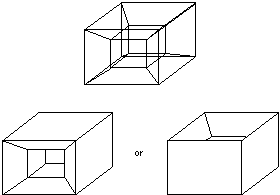
- drátový, „wire-frame“ model
- Implementace: seznam vrcholů + seznam hran (obsahuje ukazatele do seznamu vrcholů)
Nelze jednoznačně interpretovat (viz. obr.), ale vhodné k vytvoření náhledu, pro prozkoumání vnitřku tělesa.
Plošková reprezentace
Implementace: seznam vrcholů + seznam hran + seznam ploch (pořadí vrcholů v poli: counter clockwise)
Vhodná pro vykreslování zohledňující viditelnost.
Strukturovaná plošková reprezentace
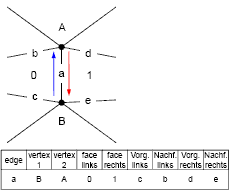
- Baumgart: Okřídlená hrana (winged edge)
- vhodné pro manifoldy
- je snadné odvodit mnoho topologických informací
- Pro nonmanifoldy: půlhrana
Bodová reprezentace
Je množina povrchových bodů (většinou získány digitálním snímáním reálných objektů). Data v jednom bodě: souřadnice, normála, barva, …
- lze je uspořádat hierarchicky a zobrazovat jenom do určité úrovně
- vysoké paměťové nároky
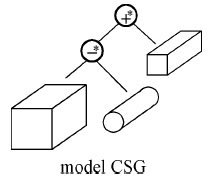
Konstruktivní geometrie těles, CSG (Constructive Solid Geometry)
Založena na reprezentaci tělesa stromovou strukturou (CSG strom), který uchovává historii dílčích konstrukčních kroků. Vnitřní uzly obsahují množinové operace, listy CSG primitivy nebo prostorové transformace. CSG primitivy: kvádr, koule, válec, kužel, jehlan, … poloprostor, plocha NURBS, …
Vhodné pro tvarování tělesa, nevhodné pro zobrazení (lze ale snadno přetransformovat např. do hraniční reprezentace).
Prořezaný CSG strom: odstraní se nevyužité větve stromu (pokud se v dané části prostoru nevyskytuje to dané těleso).
CSG tree pruning – zásadní zjednodušení CSG stromu.
Modelování pomocí deformací
Deformace je dodatečné tvarování, může být lokální nebo globální.
Barrovy deformace
- globální
- neuniformní změna měřítek: X = F_x(x), Y = F_y(y), Z = F_z(z), kde [x,y,z] je nedeformovaný, [X,Y,Z] je deformovaný bod
Základní deformace:
Změna měřítek (Scale)
Zeslabování, zašpičatění (tapering)
ve směru osy z:
X = r_x . x
Y = r_y . y
Z = z
r_x, r_y jsou lineární nebo nelineární zeslabovací funkce
Zkroucení (twisting)
Ohýbání (bending)
- složená transformace
- ohýbací zóna - aplikuje se kruhová deformace
- vnější zóny tělesa - dochází k posuvu a natočení
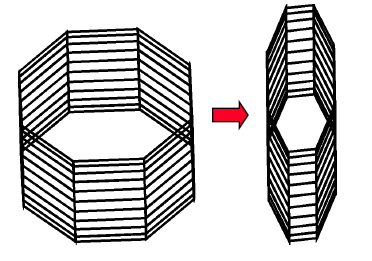
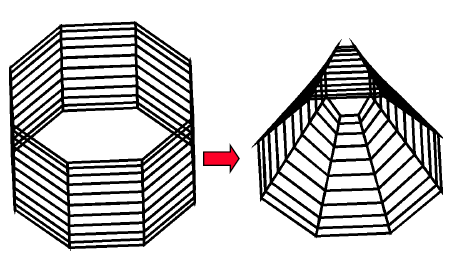
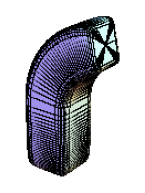
Volné tvarování těles (FFD, Free-Form Deformation)
Lze aplikovat na hraniční i na CSG modely, plochy, části ploch v prostoru. Idea je následující: obejkt z elastického materiálu vložíme do formy ve tvaru hranolu a prázdný prostor zalijeme materiálem. Pak aplikujeme sadu transformací na hranol, s tím současně deformujeme i samotný objekt.
Postup:
Máme souřadnicový systém O, X, Y, Z, zavedeme pomocný souřadnicový systém X_0, bázi tvoří vektory S, T, U, které vymezují rovnoběžnostěn (nemusí být kolmý). Rovnoběžnostěn obsahuje objekt nebo jeho část. Bod X = [x, y, z] má v lokálném souřadnicovém systému X_0 souřadnice [s, t, u] a platí: X_0 + s . S + t . T + u . U
s = {T x U(X-X_0)}/{T x U . S}
t = {S x U(X-X_0)}/{S x U . T}
u = {S x T(X-X_0)}/{S x T . U}
V prostoru rovnoběžnostěnu vytvoříme pravidelnou mřížku řídících bodů P_ijk.
Prostor zdeformujeme přemístěním řídících bodů.
Pro určení změněné pozice bodu objektu se nejprve určí lokální souřadnice bodu, pak poloha bodu ve světových souřadnicích, výslednou polohu ovlivní jednotlivé řídící body s určitou váhou (např. lineární interpolací) – měla by zaručit požadovanou hladkost (spojitost) objektu, např. pomocí Bernsteinových polynomů.
- deformovaný parametrický povrch zůstane parametrickým povrchem, deformované parametrické křivky zůstanou parametrickými křivky.
- FFD je možné aplikovat postupně
- hlavním aspektem je udržet předepsanou spojitost navazujících deformovaných a nedeformovaných oblastí
- některé operace CAD systémů nelze použít, např. zaoblování ostrých hran, svařování, …
- nevýhoda: rozhraní mezi deformovanou a nedeformovanou oblastí leží v rovině
Zdroj
Žára, Beneš, Sochor, Felkel. Moderní počítačová grafika. Computer Press, Brno, 2004. ISBN: 80-251-0454-0