Obsah
Zadání
Lokální a globální světelné modely, vlastnosti materiálu, Cook-Torrance, BRDF. Textury povrchové a objemové. Globální výpočet osvětlení, deterministické a stochastické metody, sledování světelných cest.
Materiály
V počítačové grafice jsou pro zobrazování klíčové vlastnosti ovlivňující vzhled objektů označovány pojmem Materiál. Důležitou vlastností je směr odrazu příchozího světla. Ten můžeme popsat dvěma kvalitami: difuzní a spekulární typ odrazu světla. Obvykle mají materiály nějakou kombinaci obou typů. 
V počítačové grafice (OpenGL)
Obvykle mají materiály tyto vlastnosti:
- Odrazivost pro rozptýlené světlo (Ambient) - nelze určit směr dopadu, světlo je rovnoměrně odraženo do všech směrů.
- Odrazivost pro difůzní světlo (Diffuse) - dopadá z jednoho směru, odrazí se rovnoměrně do všech směrů.
- Odrazivost pro odlesky (Specular) - dopadá z jednoho směru a odráží se také v jednom směru.
- Vyzářené světlo (Emissive) - některé předměty září, avšak v OpenGL nejsou uvažovány jako světelné zdroje. Pouze se mění jejich barva.
Všechny tyto charakteristiky materiálu jsou vynásobeny s odpovídajícími světelnými složkami a výsledky jsou sečteny.
Příklady
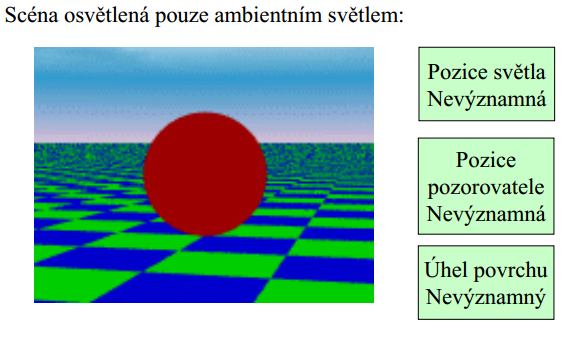
pouze ambientní světlo  ambientní a difusní světla
ambientní a difusní světla  pouze odlesky
pouze odlesky  ambientní světlo a odlesky
ambientní světlo a odlesky  difusní světlo a odlesky
difusní světlo a odlesky  všechny složky
všechny složky 
Lokální a globální světelné modely
Základní myšlenky:
Světlo putuje od světelných zdrojů ke kameře. Navrhujeme algoritmus, který napodobuje tyto světelné cesty, pokud jsou dány:
- geometrie
- materiály
- světelné zdroje
- kamera
Jednoduché modely
Empiricky založené modely.
Ambientní světlo
Objekty, které nejsou přímo osvětlené, jsou většinou také viditelné – např. podlaha místnosti, spodní povrch desky stolu. To je způsobeno nepřímým osvětlením od zdrojů světla, které se odráží od okolních povrchů. Tento jev aproximujeme trikem Ambientní světlo (všesměrové konstantní osvětlení). Nemá žádné prostorové a směrové charakteristiky; osvětluje všechny povrchy stejně. Množství odraženého světla závisí na vlastnostech povrchu.
-barva povrchu (RGB)
- koeficient ambientního světla (0..1)
Difúzní světlo
Ideální difúzní odražeč je na mikroskopické úrovni velmi drsný povrch (např. školní křída). Vzhledem k mikroskopickým variacím je příchozí světlo se stejnou pravděpodobností odraženo do libovolného směru v obklopující hemisféře.
Lambertův zákon
Ideální difúzní povrchy odrážejí světlo podle Lambertova zákona:
Energie odražená malou částí povrchu od světelného zdroje v daném směru je přímo úměrná kosinu úhlu mezi tímto směrem a normálou povrchu. 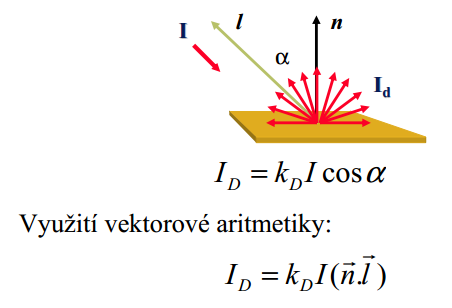
Odražená intenzita tedy závisí pouze na orientaci povrchu vzhledem ke světelnému zdroji (cosinus úhlu): 

Ambientní a difúzní světlo
Pouhý součet:
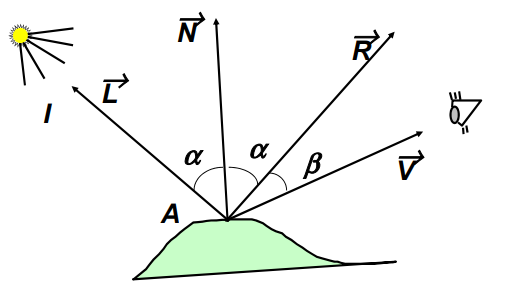
Phong – nedokonalý zrcadlový odraz
Pro modelování většiny povrchů - semi-drsné. Částečně difusní a částečně spekulární (nastavení koeficientem). Při změně místa pozorování se jeví lesklé povrchy odlišně (odlesky, zrcadlení). Světlo se odráží v „laloku“. zrcadlo = dokonale spekulární
K difuzi přidává reflexi. Ideální reflexe, odraz je symetrický podle normály.
Celkové osvětlení - Ambientní, difuzní a spekulární
Pozn.: Je potřeba upravit funkci útlumu světla vzhledem ke vzdálenosti, protože fyzikálně by mělo klesat s druhou mocninou, ale to generuje příliš velké rozsahy.
BRDF (Cook-Torrance model)
Realita není ideální – Phongův model počítá pouze s izotropními povrchy: 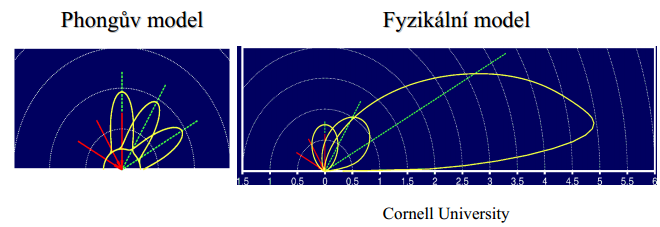

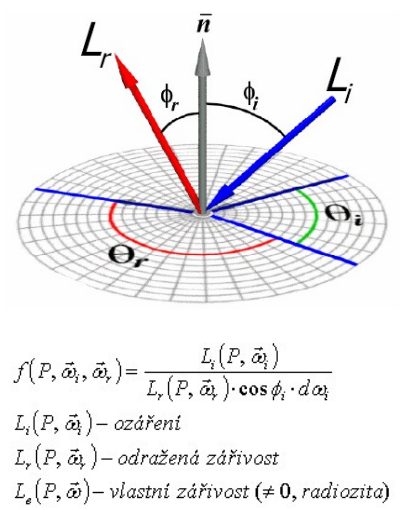
Proto vznikl Cook-Torrance lalokový model – proměnlivé odrazy pro různá místa pohledu – funkce definovaná pro každý prostorový úhel pohledu - Obousměrná odrazová distribuční funkce (Bidirectional Reflectance Distribution Function).
V každém bodu povrchu funkce vypočítá odraženou barvu pro libovolný prostorový úhel pohledu a libovolný prostorový úhel světla.
Fyzikálně založený model, realistické zobrazení (Ray-tracing). Specializace na jednotlivé efekty nebo materiály (voda, oheň, mramor, kov, látka atd.). Výpočetně náročnější. Možnost modelování světelných zdrojů. Možnost modelování anizotropních vlastností.
Globální osvětlení
Objekty se navzájem ovlivňují. Obvykle řešíme:
- více paprsků (všechny)
- odlesk (zrcadlová složka)
- barva (difúzní složka)
- polostíny (viditelnost)
Záře je podél paprsku konstantní – neubývá ani nepřibývá.
Modely vychází z řešení BRDF - obecně 4 (!) parametrická funkce: 
BRDF je anizotropní – pokud těleso otočíme, může odrážet jiné množství světla (např. směrově leštěný kov). To ale obvykle zanedbáme, takže potom má BRDF pouze 3 parametry.
Vlastnosti BRDF:
- funkce BRDF je normalizovaná - množství odražené energie bude menší než (nebo rovno) množství dopadající energie
- BRDF je lineární vzhledem k záření - energie přicházející z různých směrů přispívá nezávisle aditivně k výsledné odražené energii
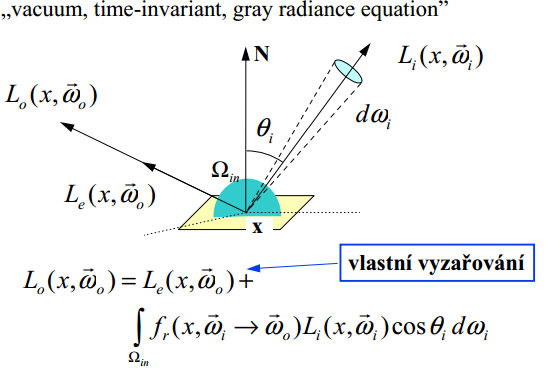
Zobrazovací rovnice
Možnosti definice zobrazovací rovnice globálního osvětlení.
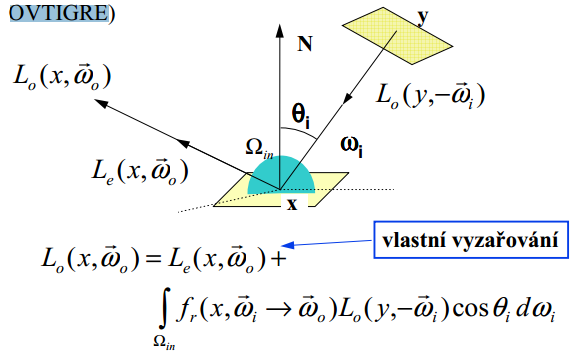
VTIGRE
OVTIGRE
Klasifikace metod řešení zobrazovací rovnice
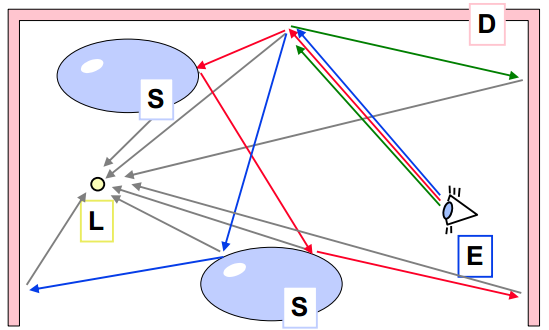
Podle cest světla, které mohou postihnout: 
- zdroj světla L („light”)
- difusní odraz D („diffuse”)
- lesklý odraz S („specular”) - odraz podle Lambertova zákona (všesměrový)
- idealizovaný zrcadlový odraz SM - směrový odraz, odlesk - směrová část BRDF
- oko pozorovatele E („eye”)
Např. Klasická zobrazovací metoda: stínování s odlesky a vrženými stíny (např. Phongův model) – jen přímé osvětlení, často se ignoruje výpočet vržených stínů ⇒ .
Metody konečných prvků
Pohledově nezávislé. Neobsahují šum (oproti MC).
Dělení scény je paměťově náročné. Získání konfiguračních faktorů je výpočetně náročné. Během iterací se může hromadit chyba.
Radiozitní metoda
C. Goral, ‘84
Zanedbává směrovost odrazu. Řešení - rovnovážný stav (konvergence) metodou konečných prvků. Nezobrazuje lesklé odrazy světla.
Předpokládáme ideálně difúzní povrchy – BRDF není závislá na vstupním a výstupním úhlu – výstupní zář Lo(x, ω) nezávisí na směru ω.
Nerozlišuje primární a sekundární zářiče. Vícenásobné difúzní odrazy. Závisí na kvalitě sítě ploch a elementů. Pohledově nezávislé řešení.
světelné cesty:
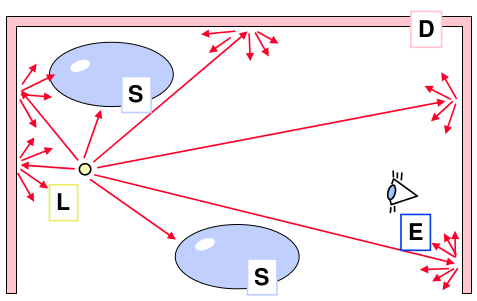
Stochastické metody
Dávají přesné výsledky. Není potřeba dělení scény. Lze řešit komplexní scény (BRDF i modely).
Obsahují šum. Pomalá konvergence. Řešení pro jeden konkrétní pohled.
Zpětné sledování paprsku
eye ray-tracing, forward ray-tracing, visibility tracing, T. Whitted, ‘80
BRDF udává váhu sekundárního paprsku lesklé plochy: zrcadlový paprsek má obvykle největší váhu, a proto ho sleduji dále.
Difúzní plochy: vše má stejný příspěvek ⇒ nepokryté cesty nahradíme ambientní složkou. První lesklý odraz se počítá přesně, ostatní se nahrazují ideálním zrcadlovým odrazem.
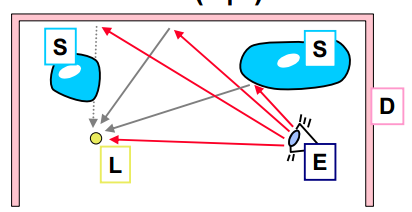
Počítá pouze s nejvýznamnějšími příspěvky odráženými difúzně (stínovací paprsky) a zrcadlově (odražený a lomený paprsek). Nepostihuje nepřímé osvětlení, měkké stíny,…
Vzorkování při sledování paprsku:
- Jediný vzorek, bod - Vystřelení paprsku středem pixelu. Náchylné k aliasu.
- Super-vzorkování pro anti-aliasing – Vystřelení několika paprsků pixelem a zprůměrování. Lze použít pravidelnou mřížku, náhodné, roztřesené nebo Poissonovské rozložení paprsků
- Adaptivní super-vzorkování – Vystřelení paprsků pixelem, ověření variance hodnot. Pokud jsou dostatečně podobné, pak konči. Jinak vystřelí další paprsky. Kompromis mezi nežádoucími artefakty aliasu a méně nežádoucími (snesitelnějšími) artefakty šumu.
Distribuované sledování paprsku
distributed ray-tracing, R. Cook, ‘86
Odhad lokálního integrálu metodou Monte Carlo - vzorkování prostorového úhlu. Počítá měkké odrazy, stíny, hloubku ostrosti,… Sekundární paprsky jsou distribuovány s ohledem na BRDF. Všechny lesklé odrazy se odhadují korektně.
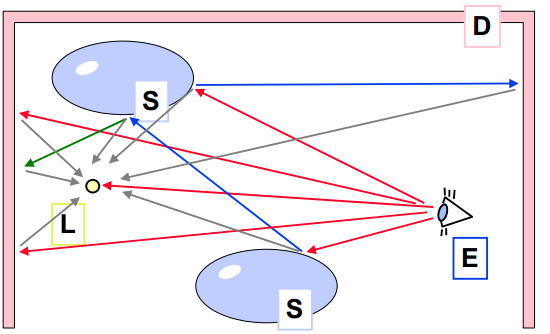
Sledované cesty:
Sledování světelných cest
(Monte Carlo) Path Tracing - MCPT, J. Kajiya, ‘86
Odhad globálního integrálu metodou Monte Carlo - výpočet náhodné cesty („náhodné procházky”). Jednosměrné i obousměrné varianty. Postihuje nepřímé osvětlení vyšších řádů.
Ideálně zobrazená scéna = všechny světelné cesty vycházející ze zdroje a dopadající do oka.
- směrem ze světelného zdroje
- přicházející do oka
- kombinace předchozích postupů
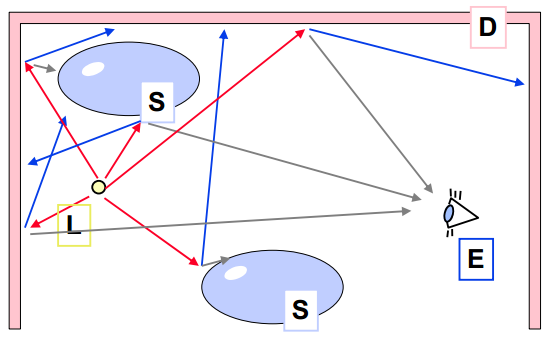
Sledování cest od pozorovatele
„sbírání energie“
Sledujeme paprsek z oka do prostředí a sbíráme světelné příspěvky. Jeden sekundární paprsek je distribuován náhodně podle BRDF včetně difusních ploch. Tzv. náhodná procházka, konec řídí ruská ruleta. Procházku několikrát opakujeme, např. dokud je velký rozptyl návratových hodnot.
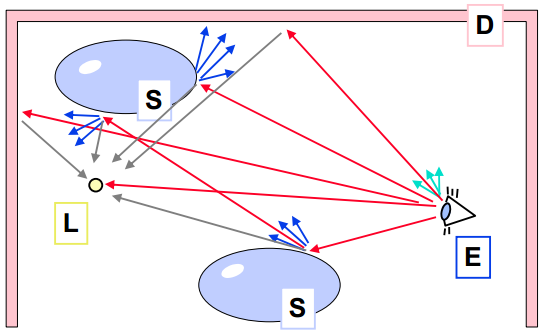
Sledované cesty:
Výsledná hodnota primárního paprsku je dána půlkulovým integrálem (viz. odrazová rovnice).
Dáno: odrazové vlastnosti ploch, polohy světelných zdrojů.
Odhad integrálu rozdělíme na dvě části:
- část odpovídající světelným zdrojům – stínovací paprsky - přímé osvětlení
- zbytek půlkulového integrálu – sekundární paprsky generované podle BRDF - nepřímé osvětlení
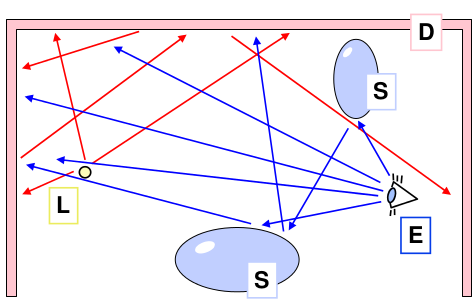
Sledování světla
Dutre&Willems ‘95
MC sledování světla je duální ke sledování cest. Sledování začíná ve zdroji (světlo vystřelí energii). Na zasažené ploše se generuje paprsek směřující k pozorovateli (test viditelnosti osvětleného místa). Odražený paprsek se generuje náhodně podle
BRDF (světlo se šíří dále…). Patří mezi tzv. metody vystřelování energie.
Obousměrné sledování cest
Veach&Guibas ’95, Lafortune&Willems ‘93
Kombinuje sledování cest a sledování světla. Po několika náhodných krocích ze zdroje a od pozorovatele se provede deterministický krok, který spojí konce (nebo i vnitřní body) obou cest, pokud jsou vzájemně viditelné. Lepší konvergence než u předcházejících metod. 
Vícekrokové metody
Kombinace radiozitních metod (difusní odrazy) a sledování paprsku (lesklé odrazy). Většinou se tyto dva přístupy střídají (algoritmus se dělí na jednotlivé „průchody“ nebo kroky).
- Radiozitní přístup řeší nepřímé difúzní osvětlení
.
- Sledování paprsku počítá lesklé odrazy
. Navíc se používá pro konečné zobrazení.
Příklad: Jednoduchá dvoukroková metoda
- klasická radiozitní metoda:
- výpočet osvětlení na všech ploškách scény. Tento krok není závislý na pozici pozorovatele.
- zobrazení sledováním paprsku:
- nepočítají se stínovací paprsky ⇒ velká rychlost. Místo světelného modelu se používá předem spočítaná radiozita. Tento krok závisí na úhlu pohledu.
Textury
Textura je popis detailní struktury povrchu a materiálu objektu, nezávislý na jeho geometrii. Jeden vzorek textury nazýváme texel.
Obvykle mění difúzní barvu objektu (ne zrcadlové efekty).
V některých aplikacích i další vlastnosti:
- spekulární barva Phongova odrazu
- směry normál (bump-mapping), nahrazení složité (mikro)geometrie
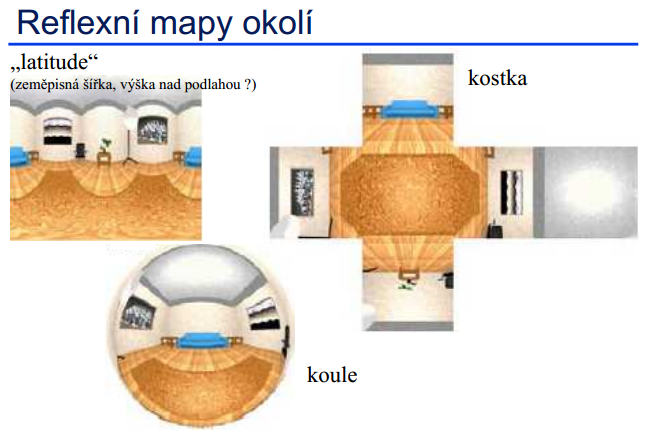
- příchozí světlo (mapy okolí, neboli reflexní mapy)
- průhlednost
- optické vlastnosti povrchu (difuze, odrazivost)
- Zrcadlení okolí
- Osvětlení
- atd.
Obecně mohou být textury libovolných dimenzí. Běžně:
- 2D – popisují pouze povrch objektu, problémy navazování
- 3D – spojitě popisují prostorové rozložení vlastností v celém objemu objektu (dřevo, mramor)
- 4D – jsou to 3D textury s časovou změnou, umožňují dynamické změny (oheň, mlha)
Možnosti reprezentace
- Předem připravené pole dat (tabulka, bitmapa) - především 2D textury. Skutečná (přírodní) data, obrázky, etikety. Pro větší kvalitu (spojitost) zavádíme různé typy interpolace.
- Textury definované algoritmem (předpisem) - jednoduché geometrické tvary (fraktály, stochastické funkce (šum, turbulence)).
- Smíšené metody (předem spočítaná tabulka) - náročné modelovací metody (reakční difúze,…)
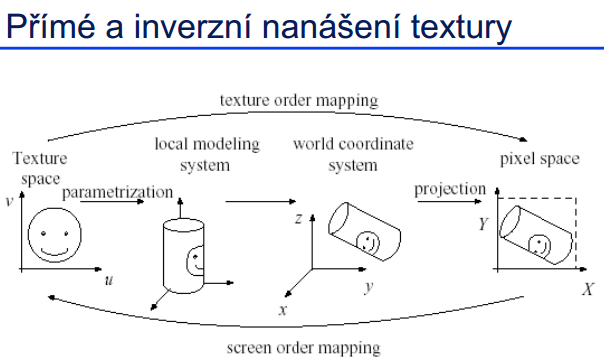
Texturování
Texturování je proces nanášení textur na geometricky definovaný povrch objektu. Texturování pomáhá odlišovat a rozpoznávat jednotlivé objekty a zvyšuje úroveň realističnosti jejich zobrazení.
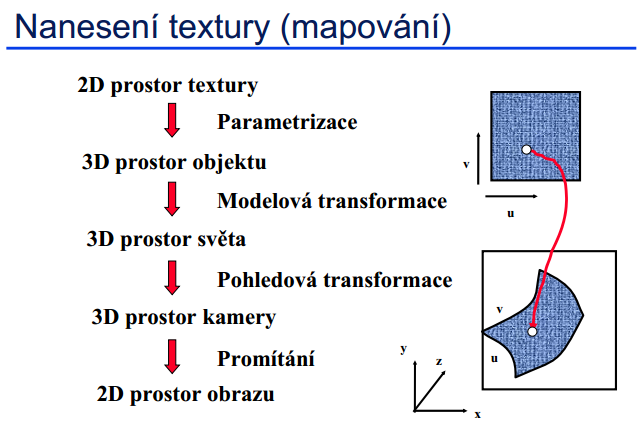
Postup nanášení textury
Vybraná textura se musí zvětšit/zmenšit na velikost polygonu filtrováním. Je přitom vhodné interpolací zabránit vzniku aliasu, a to jak v časové, tak i prostorové oblasti.
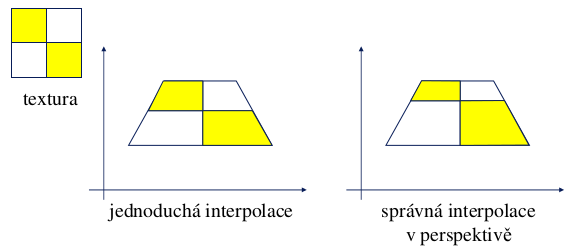
Interpolace textury
Metody:
- bez interpolace (zaokrouhlení) - nejjednodušší a nejrychlejší metoda. Pokud se rozlišení obrázku blíží rozlišení textury, vznikají výrazné a nepříjemné artefakty (Doom)
- bilineární interpolace - zajišťuje spojitost obrazové funkce (C0).
- polynomiální interpolace (např. spline funkce) - spojitost vyšších řádů (u bikubické až C2). Výpočetně náročná (kombinace 9-16 hodnot ve 2D)
Pro efektivní reprezentaci textury v různých předpočítaných rozlišeních zavádíme Mip-Map filtrování. Interpolujeme vždy mezi nejbližším větším a nejbližším menším rozlišením. 
Mapování textur na objekty
Inverzní mapování přes pomocné objekty
U většiny běžných objektů není možné nalézt jednu analytickou funkci popisující povrch (aby bylo možno inverzní mapování textury). Proto musíme provádět mapování po částech (plochy, polygony). Spojitost částí zajistí Texturovací souřadnice. Texturu nanášíme inverzně na jednoduchý pomocný (obalový) objekt (kvádr, válec, kouli,…) okolo objektu a následně mapujeme z pomocného objektu na výsledný. 
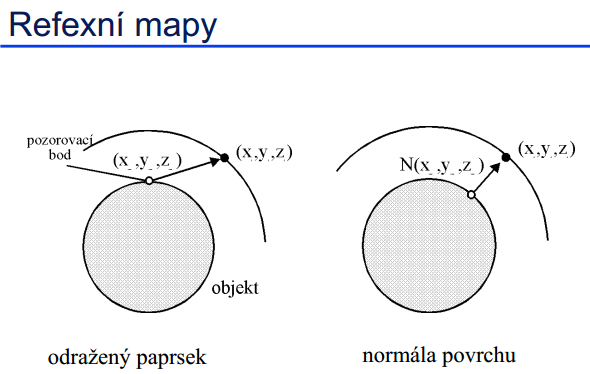
Reflexní mapování
Přes pomocné objekty můžeme také snadno nanášet odrazy okolí: 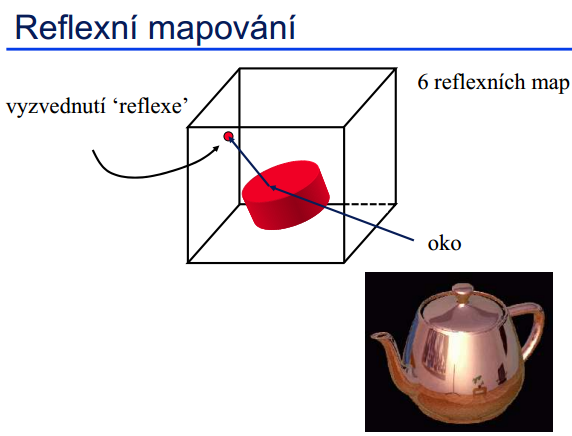
Různé možnosti vyzvednutí barvy z pomocného objektu (podle aplikace): 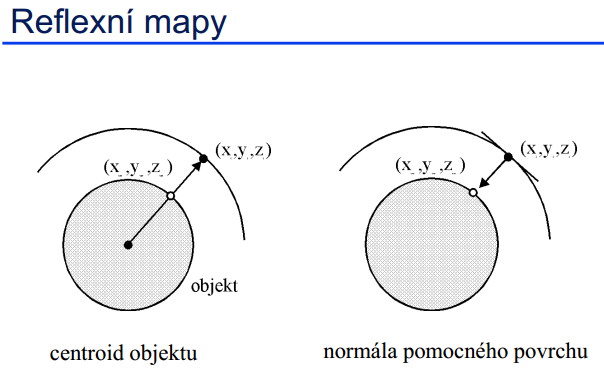
Bump mapping
Efekt plastického, hrbolatého povrchu. Nemění se skutečně geometrie objektu. Vhodné pro simulaci relativně drobných nerovností povrchu. Podle gradientu v textuře se modifikují pouze normály povrchu při výpočtu osvětlovacího modelu. Obrysy objektu jsou proto stále hladké. 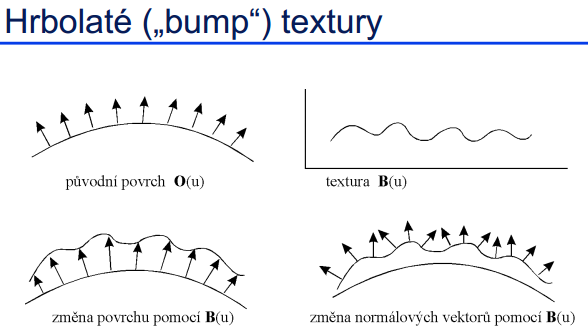
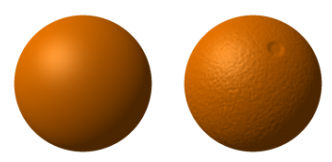
Displacement mapping
Efekt plastického, hrbolatého povrchu. Skutecně se mění geometrie objektu, posouvají se vrcholy. Vhodné pro simulaci relativně větších nerovností povrchu. Podle gradientu v textuře se posouvají pozice bodů povrchu, ve směru normály. Obrysy objektů jsou změněny. 
3D textura
[x,y,z] → barva (odrazivost, atd.). Zachycuje změny veličin uvnitř tělesa, napodobuje vnitřní strukturu materiálu (dřevo, mramor, …). Není třeba počítat inverzní mapování. Pro napodobení přírodních jevů se využívají tzv. šumové funkce – pseudonáhodné spojité “vrásnění”.
Algoritmické a smíšené textury
Jednoduché geometrické tvary, vzorky – šachovnice, pravidelné pruhy,… nebo napodobení přírodních tvarů. Často se využívají pseudonáhodné algoritmy (syntéza spojité šumové funkce) – fraktály, turbulence (mraky, špína, ..), reakční difúze (napodobení kůže a srsti zvířat), prostorové náhodné textury (dřevo, mramor,…).
Perlinův šum
Tato metoda generování šumu funguje na součtu stejné šumové funkce, avšak o různé intenzitě a v různém měřítku. Pro takovouto šumovou funkci se často používá náhodný, deterministický generátor. Výsledkem součtu šumových funkcí je šum, kterým je možné napodobit rozličné přírodní věci, nejčastěji oblaka, vodu, dřevěné materiály a mramor.
Pořadí při sčítání se nazývá oktáva. V každé oktávě má šumová funkce různé měřítko a intenzitu. Měřítko lze udávat frekvencí, tedy počtem opakování na jednotku. Intenzitu v tomto případě nazýváme amplitudou.
Perlinův šum je realizován jako funkce buď (x,y,z) nebo (x,y,z,čas), která využívá interpolaci mezi sadou předem vypočítaných vzestupných vektorů, pro konstrukci hodnoty, která se mění náhodně v závislosti na prostoru a/nebo čase.
Spektrum je omezené na jednu oktávu [f-2f]
– efektivní implementace
Použité zdroje
doc. Ing. Přemysl Kršek, Ph.D., Ing. Michal Španěl : IZG - Základy počítačové grafiky, slajdy. 2008. Ústav počítačové grafiky a multimédií, Fakulta informačních technologií, Vysoké ucení technické. Brno.
Josef Pelikán, Jiří Sochor : PB009 - Základy počítačové grafiky, slajdy. 2012. Fakulta informatiky, Masarykova Univerzita. Brno.
Josef Pelikán, Jiří Sochor : PA010 - Počítačová grafika, slajdy. 2012. Fakulta informatiky, Masarykova Univerzita. Brno.
Wikipedie: Otevřená encyklopedie: Perlinův šum [online]. c2013 [citováno 8. 04. 2013]. Dostupný z WWW: <http://cs.wikipedia.org/w/index.php?title=Perlin%C5%AFv_%C5%A1um&oldid=9942320>