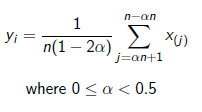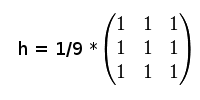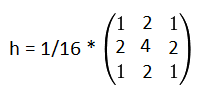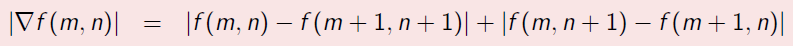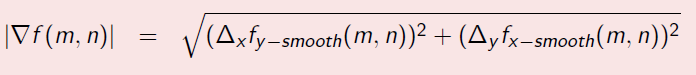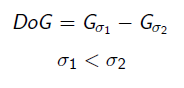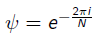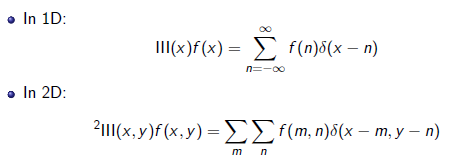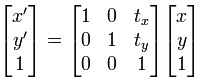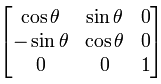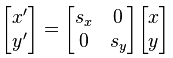Obsah
Zadání
Zpracování rastrového obrazu. Histogram, ekvalizace podle histogramu. Prahování, redukce úrovní jasu (barev). Lineární a nelineární filtry. Detekce hran. Diskrétní Fourierova transformace při úpravách obrazu. Geometrické transformace obrazu, filtrování, převzorkování, vyhlazování. (PA010, PA171)
Rastrový obraz
Rastrový obraz je matice n x m pixelů (1 bit → černobílý, monochromatický).
- indexový mód - hodnota pixelu je ukazatel do tabulky - barevné palety (color palette), např. gray scale
- true color, static gray - pixel obsahuje přímo hodnotu intenzity
- direct color - pixel ukazuje do 3 palet (R, G, B)
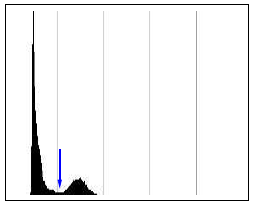
Histogram
Histogram kvantifikuje množství a frekvenci barev obsažených v obraze, tj. hodnota histogramu H pro index i odpovídá počtu pixelů v obraze, které mají intenzitu i. (Šedotónní obraz má 1 histogram, barevný 3)
Bílý bod je nejsvětlejší bod v histogramu, černý bod je nejtmavší.
Poznámka: Při fotografování → technicky dobrý obraz využívá celou škálu intenzit.
Změny histogramu
Zvýšení/snížení jasu, změny kontrastu - pomocí korekční křivky přímo na histogramu.
Ekvalizace histogramu
Je to vyrovnání, změna jasu. Cílem je najít mapovací funkci, která rozloží hodnoty histogramu rovnoměrně. Ideálně histogram obsahuje všechny hodnoty zastoupené stejnou četností d = (n * m)/max, kde max je maximální intenzita pixelů v obraze s rozlišením n x m. Lze provádět i lokálně (např. v astronomii).
Ekvalizace v barevném prostoru
Buď se provádí na každém barevném kanálu odděleně, nebo se obraz převede do jiného barevného prostoru, např. YIQ. Použití: fotografie proti světlu nebo v šeru.
Prahování (Thresholding)
Jedna z metod binární segmentace
Rozdělení jasové složky na 2 části a nahrazení jedinou hodnotou: 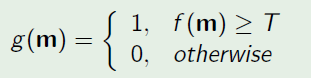 kde T je práh (nejčastěji je vhodné zvolit medián nebo 50 procent šedé). Prahováním se obraz (f) převede do binární reprezentace (g).
kde T je práh (nejčastěji je vhodné zvolit medián nebo 50 procent šedé). Prahováním se obraz (f) převede do binární reprezentace (g).
Ohraničené prahování:
i_n = i pro 0 <= i < D L pro D <= i < T H pro T <= i < U i pro U <= i <= max
Dělení:
- globální
- lokální
- dynamické/adaptivní
Jak najít vhodný práh automaticky?
- V bimodálním histogramu (2 lokální maxima):
- V unimodálním histogramu:
Gama korekce
CRT monitory → nelineární časová odezva, ovlivňuje dithering
i' = i^(1/gamma), gamma = 2.5 +- 0.3 (závislá na typu obrazovky)
Lineární a nelineární filtry
Šum je nová informace, která byla k původní přidána pořizovacím zařízením nebo během transportu (aditivní vs. multiplikativní). Druh šumu se určuje podle frekvenční charakteristiky po Fourierově transformace. Bílý šum má frekvenční spektrum dokonale vyrovnané - matematická abstrakce
Typy:
- Poissonův (photon-shot noise)
- Aditivní - g=f+n, kde f je originální funkce, n šum
- Impulsní - př. sůl a pepř
Odstranění šumu (Filtrace)
Za šum jsou považovány velké změny intenzit v sousedících pixelů. Potlačí se buď konvolucí (lineární) nebo lokální statiskitou okolí pixelu (nelineární).
Nelineární filtry
Medián filter
Není konvolucí! Vhodné pro odstranění impulsního šumu, avšak narušuje tenké čáry. Okolí nemusí být čtvercové.  y(i) = med(x_i-k, … x_i, … x_i+k)
y(i) = med(x_i-k, … x_i, … x_i+k)
Jinak:
Pro všechny pixely [i, j] v obrazu A
1. Načti body z intervalu [i-k, j-k][i+k, j+k] do pole M délky l = (2k+1)^2
2. Seřaď pole M
3. Výstupní obraz B[i,j] = M[(l-1)/2]
Max filter
y(i) = x(n)
Min filter
y(i) = x(1)
Alpha trimmed mean filter
Lineární filtry
Konvoluce
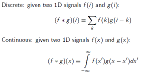
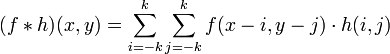 g, h - konvoluční jádro (okno, které se posouvá po obraze)
g, h - konvoluční jádro (okno, které se posouvá po obraze)
Vlastnosti konvoluce:
(f*g)(i) = (g*f)(i)
( (f*g)*h )(i) = ( f*(g*h) )(i)
(kernel separability) g je separabilní, pokud platí g = g_row * g_col^T
Konvoluce s 2D jádrem O(n²), konvoluce s 2 1D jádrami O(n).
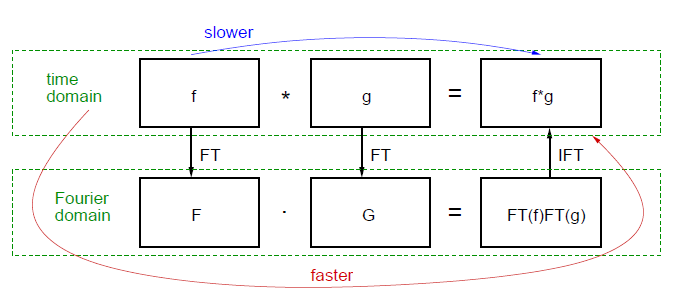
Konvoluční teorém:
F(f*g) = F(f).F(g)
F(f.g) = F(f)*F(g)
F - Fourierova transformace
f, g - obrázky
Obyčejné průměrování
Filtrace pomocí obyčejného průměrování ve Fourierově doméně odpovídá násobení funkcí, která odstraní frekvence vyšší než určitá hodnota (odřezání vysokých frekvencí - low-pass filtering, potlačení s váhou).
- Ideal Low-Pass Filter: H(u,v) =
1 pro √(u²+v²) ≤ D0,
0 pro √(u²+v²) > D0,
jedná se o válec s poloměrem D0 a výškou 1.
Ostření obrazu ve frekvennční doméně → high-pass filtering
- Ideal High Pass Filter: H(u,v) =
0 pro √(u²+v²) < D0,
1 pro √(u²+v²) >= D0
Gaussův filter
Detekce hran
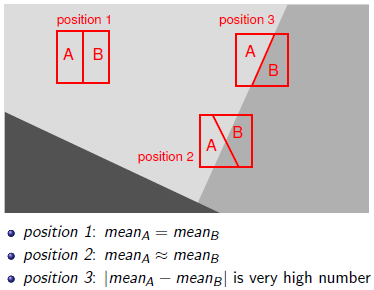
Hrana (edge) v diskrétním obraze je výrazná změna intenzit sousedních pixelů, vysokofrekvenční informace. Je určena gradientem (vektor ukazující směr největšího přírůstku funkce):
∇f(x,y) = (∂f(x,y)/∂x, ∂f(x,y)/∂y), velikost: |∇f(x,y)| = √(∂f(x,y)/∂x)² + (∂f(x,y)/∂y)²
Založené na první derivaci
Robertsův operátor
Detekuje především hrany se sklonem 45°. Možno rozdělit na 2 složky detekující hrany v na sebe kolmých směrech. 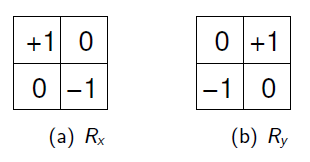
Sobelův operátor
Canny hranový detektor
Požadavky:
- Minimální počet chyb (musí být detekovány všechny hrany, nesmí být detekována místa, která hranami nejsou)
- Přesnost (poloha hrany musí být určena co nejpřesněji)
- Jednoznačnost (odezva na jednu hranu musí být jedna, nesmí docházet ke zdvojení)
Stručný postup:
- Eliminace šumu (Gaussovým filtrem)
- Určení gradientu (první derivace)
- Nalezení lokálních maxim (thinning)
- Eliminace nevýznamných hran (thresholding)
Neprodukuje spojité hrany.
Rothwell hranový detektor
Stejný jako Canny, jenom krok thinning je modifikován, aby hrany byly spojité. Topologický přístup.
Založené na druhé derivaci
Hrany se nacházejí v nulových bodech (zero crossings) druhé derivace, to jsou maxima první d
erivace.
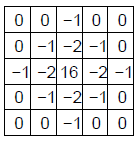
Laplaceův operátor (Δ)
Aproximuje druhou derivaci funkce. 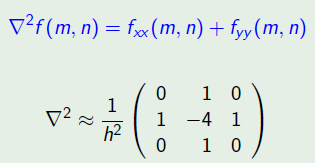
Nevýhody:
- detekuje nejen maxima, ale i minima
- citlivý na šum
- nedetekuje orientaci hrany
Výhody:
- produkuje spojité hrany
- invariantní k otáčení o násobky 45°
- orientačně nezávislý
Laplacian of Gaussian (LoG)
Difference of Gaussians (DoG)
(Template based edge detection)
Lineární
Nelineární
Diskrétní transformace
Fourierova transformace
Slouží k převodu obrazu (z prostorové domény, I) do duálního prostoru (frekvenční domény, F) a zpět. Frekvenčná doména je obecně složením nekonečně mnoha sinusových signálů s různou amplitudou, které jsou různě fázově posunuté.
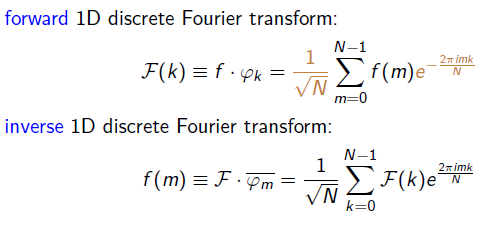
 k=0…N-1, n=0…N-1
k=0…N-1, n=0…N-1
komplexní jednotka: i = √(-1)
Eulerova formule: e^(±i2πux) = cos(2πux) ± i sin(2πux)
Mějme bod o souřadnici u = Re(u) + i Im(u). Amplitudové spektrum funkce F(u) je |F(u)| = √(Re²(u) + Im²(u)), fázové spektrum φ(u) = atan(Re(u)/Im(u)). 
FFT (Fast Fourier Transform)
Důležité vlastnosti Fourierova transformace:
1. Roztažení (stretch) funkce v prostorové doméně odpovídá opakování funkce (repetition) ve frekvenční doméně: 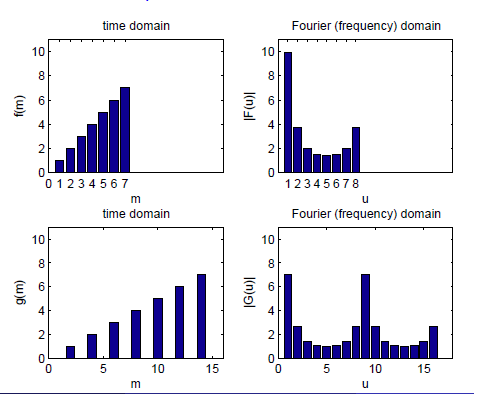 2. Posun (shift) v prostorové doméně ovlivňuje jenom fázu:
2. Posun (shift) v prostorové doméně ovlivňuje jenom fázu: 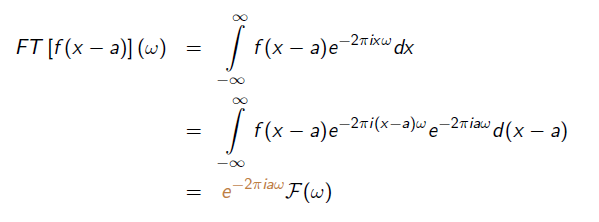
Proveďme dělení dokud je možné, tj. dostaneme se k signálu délky jednoho bodu, který je stejný bod i ve frekvenční doméně: 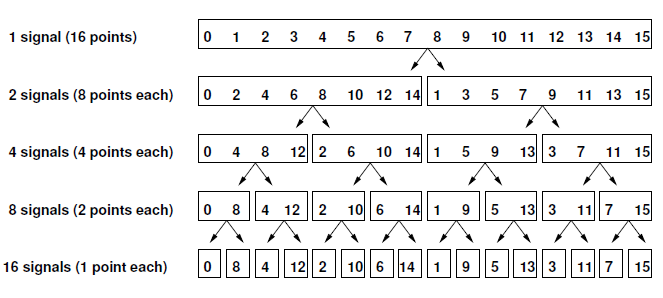
Geometrické transformace obrazu
Chceme transformovat vstupní obraz A na výstupní B. Geometrická transformace obrazu složeného z bodů [x,y] je funkce T(u,v) = [x(u,v), y(u,v)].
- Dopředné mapování - procházíme pixely A, hledáme jejich umístění v obraze B (oblast)
- Zpětné mapování - procházíme pixely B, hledáme odpovídající oblasti v A
Separabilita:
Transformace je separabilní, pokud ji lze zapsat ve tvaru T(u,v) = F(u, G(v)). F a G jsou funkce jedné proměnné. Př. Fourierova transformace.
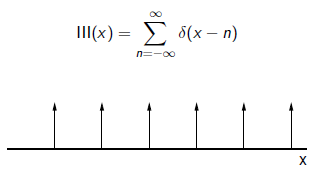
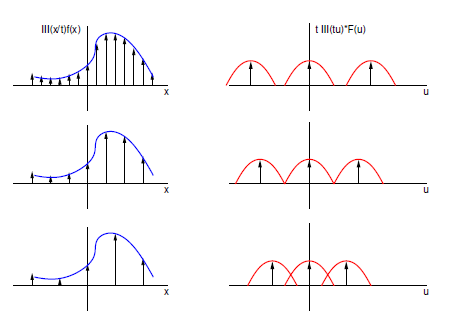
Vzorkování (Sampling)
Nyquist-Shannon theorem
Spojitou funkci je možné úplně zrekonstruovat pouze v případě, že signál je frekvenčně omezený (bandlimited) a vzorkovací frekvence je dvakrát větší než maximální frekvence signálu.
Při nesplnění těchto vlastností vzniká alias. 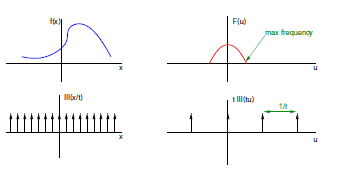
Rekonstrukce (Reconstruction)
Inverzní proces ke vzorkování, konvoluce s low-pass filterem. Zrekonstuuje originální spojitý signál z diskrétních vzorků.
Rekonstrukční filtry:
- box - nejbližší soused
- tent - lineární interpolace
- kubický B-spline - kubická polynomiální interpolace
- Gaussian
- sinc
- Lanczos - omezený sinc
Plocha pod filtrem musí být jednotková, tj. ∫ h(t) dt = 1, kde h je rekonstrukční filter.
Převzorkování (Resampling)
Lineární geometrické transformace
Posunutí (Translation)
Otáčení (Rotation)
Změna měřítka (Scale)
Zkosení (Shear)
Nelineární geometrické transformace
Warping
viz otázku č. 13
Zdroj
Žára, Beneš, Sochor, Felkel. Moderní počítačová grafika. Computer Press, Brno, 2004. ISBN: 80-251-0454-0
David Svoboda : PA171 - Digital image filtering, slajdy. 2012. Fakulta informatiky, Masarykova Univerzita. Brno.