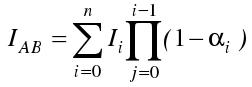Obsah
Zadání
Rekonstrukce objektů a vizualizace objemových dat. Rekonstrukce z příčných řezů, objemových a prostorových dat. Přímá vizualizace objemových dat. Vizualizace objemů a ploch. Algoritmus pochodující kostky.
Objemová data
Použití
Medicína
- (rentgenová) počítačová tomografie (CAT)
- nukleární magnetická rezonance (NMR, MRI)
- pozitronová emisní tomografie (PET)
- “single photon emission computer tomography” (SPECT)
- kombinace různých technologií (např. CAT+NMR)
Průmyslová defektoskopie
- sonogramy, rentgenové přístroje,…
Věda
- zobrazení naměřených dat – geologie, seismologie, meteorologie; molekulární chemie a biologie
- zobrazení matematické simulace – (dynamická) vektorová pole; průmyslová konstrukce, aerodynamika, meteorologie,…; astronomie, astrofyzika
- zobrazení implicitně definovaných ploch
Předmět vizualizace
Statická 3D data: forma zobrazení f: R3 → Rn. Uspokojivě lze zatím zobrazovat jen data skalární. Výjimečně vektorová (n ≤ 3), ale např. v meteorologii se měří/počítá až 30 veličin v každém bodě – lepší přehled o průběhu veličin dávají animace.
Dynamická 3D data (animace) – forma zobrazení f: R4 → Rn (x,y,z,t). Animace je složitější, uživatelem řízená (“steering”).
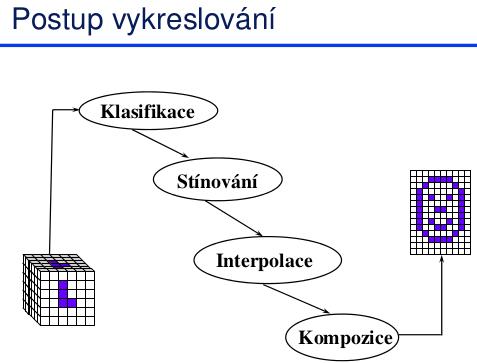
Postup při vizualizaci objemových dat
- Segmentace
- Výpočet gradientů
- Převzorkování
- Klasifikace
- Stínování
- Kompozice
Požadavky
- Názornost zobrazení – získat co nejlepší představu o zobrazované funkci (a jejím časovém průběhu). Cílem nejsou bezpodmínečně realistické obrázky.
- Interakce uživatele – (“steering”: on-line animace).
- Věrnost, pravdivost – výstup by neměl být příliš zkreslený.
- Rychlost výpočtu – pro animace minimálně několik obrázků/s.
Formáty 3D dat
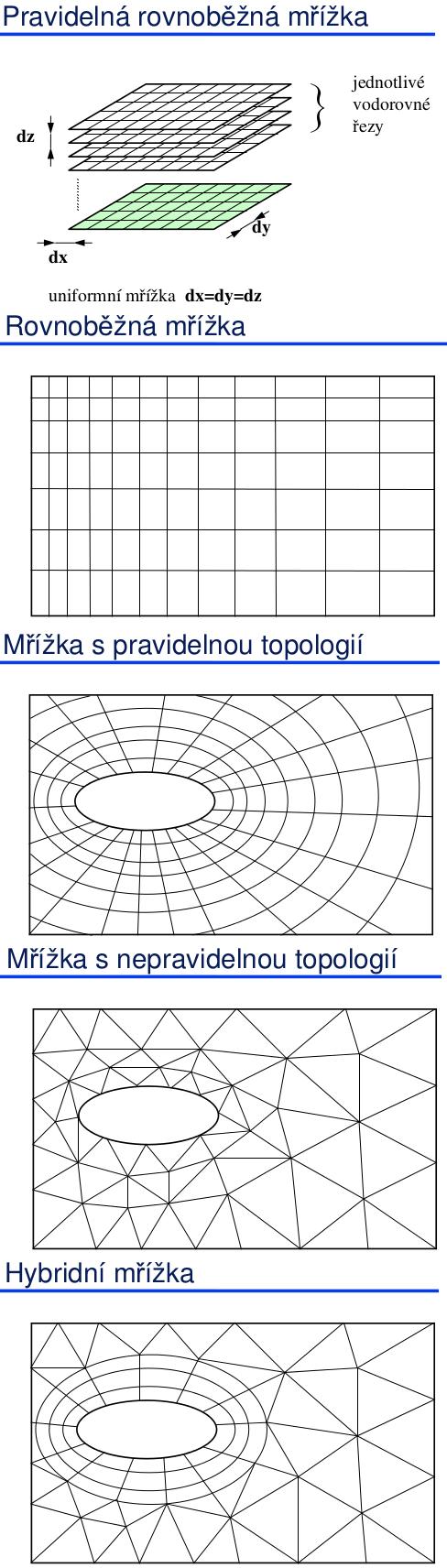
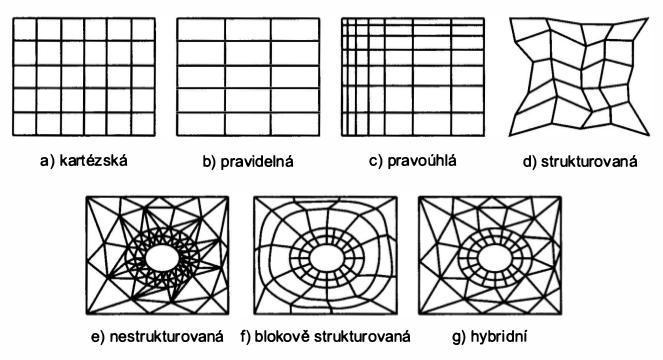
- Rovnoběžná mřížka – reprezentace maticí K * L * M a diferenčními vektory dx, dy, dz. Stěny jednotlivých buněk rastru jsou rovnoběžné, rastr nemusí být uniformní.
- Mřížka s pravidelnou topologií – reprezentace maticí K * L * M a sítí parametrických ploch Pu[], Pv[], Pw[]. Buňky mají pouze stejnou topologii (např. 6 stěn).
- Mřížka s nepravidelnou topologií – libovolně rozmístěné uzly hodnot + topologie buněk. Čtyřstěny, šestistěny (v rovině: trojúhelníky, čtyřúhelníky).
- Hybridní mřížka – kombinace pravidelné a nepravidelné topologie, viz metody konečných prvků, hybridní síť pro radiační metodu.
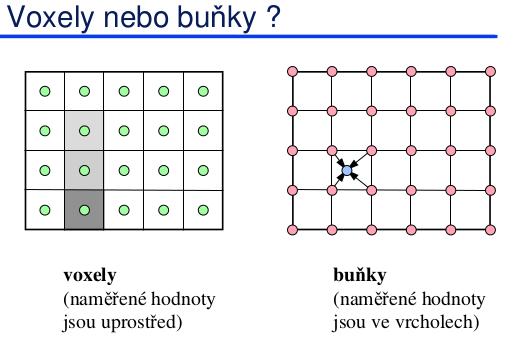
Data v pravoúhlých mřížkách můžeme chápat jako kvádry nazývané voxely, v nichž je v celém objemu hodnota konstantní. Takové dělení je obvykle příliš hrubé, proto zavádíme reprezentaci buňkovou, kde jsou ohodnoceny vrcholy jednotlivých kvádrů a hodnoty libovolných vnitřních bodů jsou získány interpolací hodnot nejbližších 8mi vrcholů (nebo 64 v případě aproximace 2. řádu).
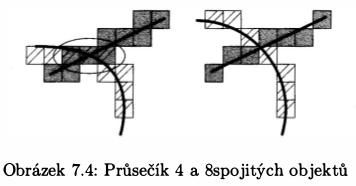
Důležitá je také specifikace spojitosti podobně jako v rastrových obrázcích, kde můžeme specifikovat spojitost jako 4 nebo 8mi okolí:
V objemových datech můžeme rozlišit možnosti spojitosti takto:
- 6-ti spojitost dotyk povolen pouze celou stěnou voxelu,
- 18-ti spojitost dotyk povolen stěnou nebo hranou (6+12),
- 26-ti spojitost dotyk stěnou, hranou nebo vrcholem voxelu (6+12+8)
Způsob, jakým jsou definovány diskrétní 3D objekty v objemu, je určující nejen při zjišťování vzájemných průsečíků objektů, ale i pro definici spojitosti zobrazovacího paprsku. Proto, pokud víme, že objekt je 18ti nebo 26spojitý, musíme použít 6spojitý paprsek, aby nedocházelo k chybné detekci povrchů. Naopak pro 6spojitý objekt (ten díry obsahovat nemůže) lze použít paprsek 18 či 26spojitý. Spojitost paprsku má podstatný vliv též na jeho délku, tj . na počet kroků, které musí při průchodu scénou vykonat.
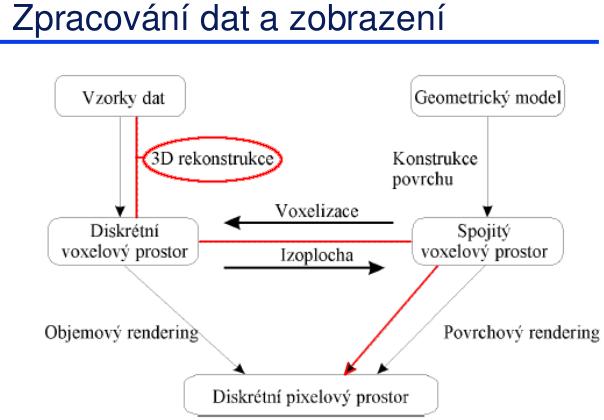
Fáze zpracování 3D dat
- Pořízení dat (měření nebo výpočet) – uvnitř snímacího zařízení (CAT, MRI) mohou již být použity některé netriviální algoritmy. Převod několika kumulativních projekčních snímků do jednoho 2D obrazu (dělá skrytý firmware).
- Úpravy a vylepšení jednotlivých řezů: 2D op. – filtrace: vyhlazování, zvětšování kontrastu. Změny kontrastu - např. automatické vyrovnávání histogramu (stejné operace na všech řezech!)
- 3D úpravy a vylepšení – úpravy formátu: přidávání dalších řezů (interpolací), převzorkování (v uniformní mřížce),…, 3D filtrace: vyhlazování, zvětšování kontrastu.
- Klasifikace dat, segmentace – medicína: různé typy tkání (kost, mozek, svalstvo, tuk, vzduch). Ruční nebo automatická (např. analýzou histogramu).
- Zobrazení dat – projekce do 2D.
Zobrazovací algoritmy - nalezení povrchu v objemových datech
Některé algoritmy převádějí objemová data do povrchové reprezentace. Velmi častým postupem je aproximace povrchů sítí trojúhelníků. Povrchy se předpokládají obvykle v místech s konstantní hodnotou vzorků. Proto se takto vzniklé sítě nazývají izoplochy (srovnej kapitolu 5.12), obdobně jako izočáry ve dvou rozměrech.
- Výpočet izoploch (surface fitting, SF) - Aproximace izoplochy sítí n-úhelníků (trojúhelníků). Výpočet není závislý na úhlu pohledu. Zobrazení klasickými metodami (HW podpora). Uživatel zadává prahovou hodnotu (i více hodnot).
- Přímé zobrazovací metody (direct volume rendering, DVR) - Většinou nepoužívají pomocná grafická primitiva. Dávají globální představu o průběhu zobrazované funkce.
Rekonstrukce izoploch
Výpočet a zobrazení jedné nebo více izoploch. Prahové hodnoty zadává uživatel. Aproximace izoplochy sítí rovinných plošek.
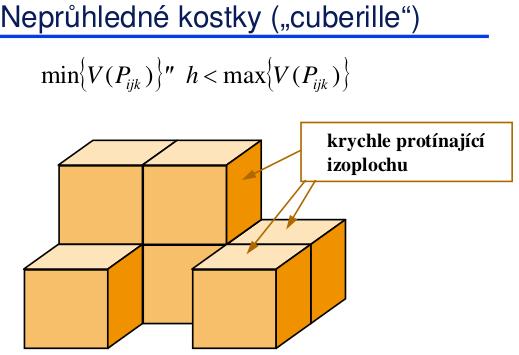
Neprůhledné kostky (“cuberille”)
Herman: 1979. Zobrazení krychlí, které protínají zadanou izoplochu – podle směru pohledu stačí kreslit pouze tři stěny krychle. Aproximace je příliš hrubá (plocha je hranatá). Pro lepší vzhled možno použít spojité stínování gradientní metodou, hranaté okraje však zůstávají. Nebo současné zobrazení několika izoploch - technika poloprůhledných ploch (kanál alfa).
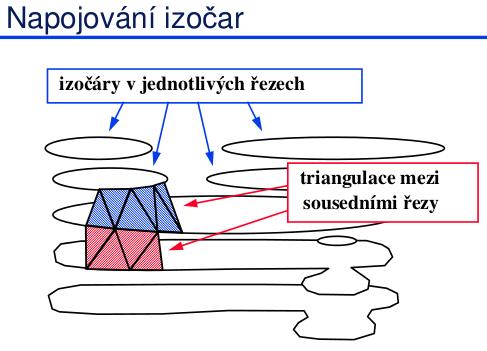
Napojování izočar (“contour connecting”)
Keppel: 1975, Fuchs: 1977, Ekoule: 1991. Výpočet izočar v jednotlivých řezech: izočára se reprezentuje jako lomená čára. Jeden řez může obsahovat několik uzavřených smyček izočáry. Triangulace izoplochy mezi dvěma řezy – trojúhelníky by neměly být příliš protáhlé.
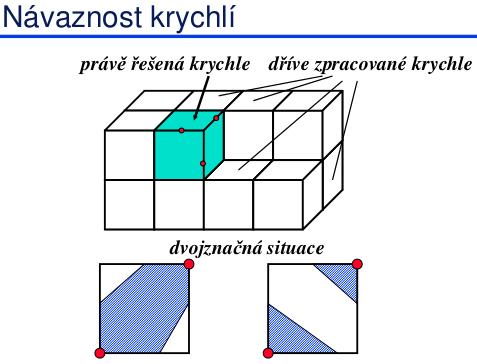
Topologicky obtížné situace: několikanásobné větvení (1:N, M:N), nejednoznačné přiřazení napojovaných izočar.
Algoritmus Ekoule, Peyrin, Odet
Zřejmě není třeba znát takto detailně. Spíše pro ilustraci.
Rozdělení na několik geometricky/topologicky odlišných případů:
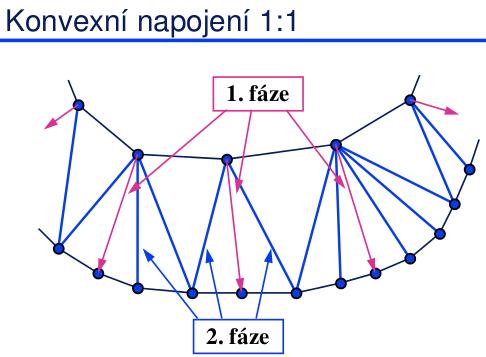
- konvexní napojení 1:1: pro izočáru s menším počtem vrcholů. Každý vrchol se spojí s nejbližším bodem naproti, efektivní algoritmus pracuje inkrementálně - hledá nejbližšího souseda v okolí naposledy přiřazeného vrcholu. Zbývající vrcholy z druhé izočáry se spojí s nejbližšími protějšky. Některé vrcholy se musí spojit se dvěma protějšími body (aby vznikla triangulace).
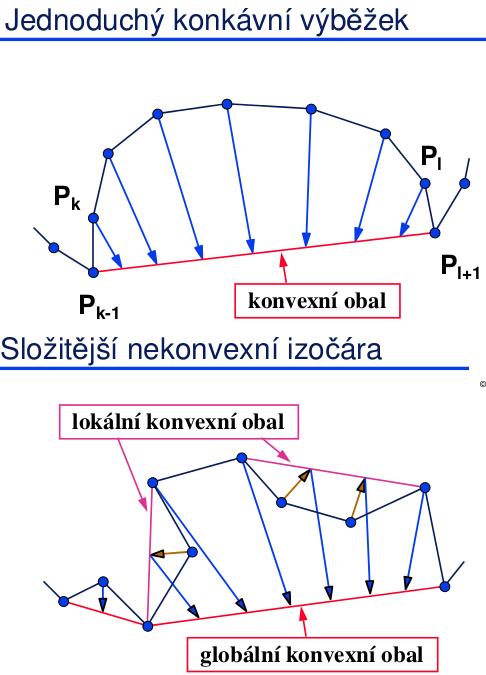
- nekonvexní napojení 1:1: přenášení vrcholů z nekonvexních úseků na konvexní obal izočáry. Hypotéza: konvexní obaly dvou sousedních izočar si budou více podobné. Přenášením se zachovává pořadí i relativní vzdálenosti vrcholů. Triangulace se provádí na konvexních obalech, hranami se potom spojí původní vrcholy izočar.
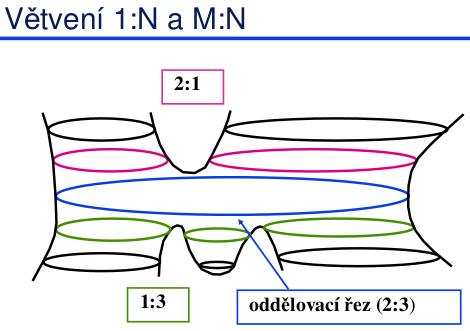
- větvení 1:N a M:N: Hierarchická transformace převádí obecný mnohoúhelník na konvexní. Zachovává počet vrcholů i jejich relativní vzdálenosti. Rekurentní formulace (hierarchický rozklad mnohoúhelníka): transformace lomené čáry Pi, …, Pj - na začátku se bere celý mnohoúhelník P1,…,PN. Výpočet konvexního obalu (i,j) - vrcholy ležící v konvexním obalu se nepřesunují. Pro každou posloupnost vrcholů Pk … Pl (k ⇐ l) neležících v konvexním obalu (i, j) se provedou následující kroky: přenesení vrcholů lomené čáry Pk-1 … Pl+1 do jejího konvexního obalu (k-1, l+1). Rekurentní vyvolání popisovaného algoritmu. Přenesení vrcholů Pk až Pl na úsečku Pk-1 Pl+1, body Pk-1 až Pl+1 již leží v konvexním obalu (i, j), zachování relativních vzdáleností sousedů.
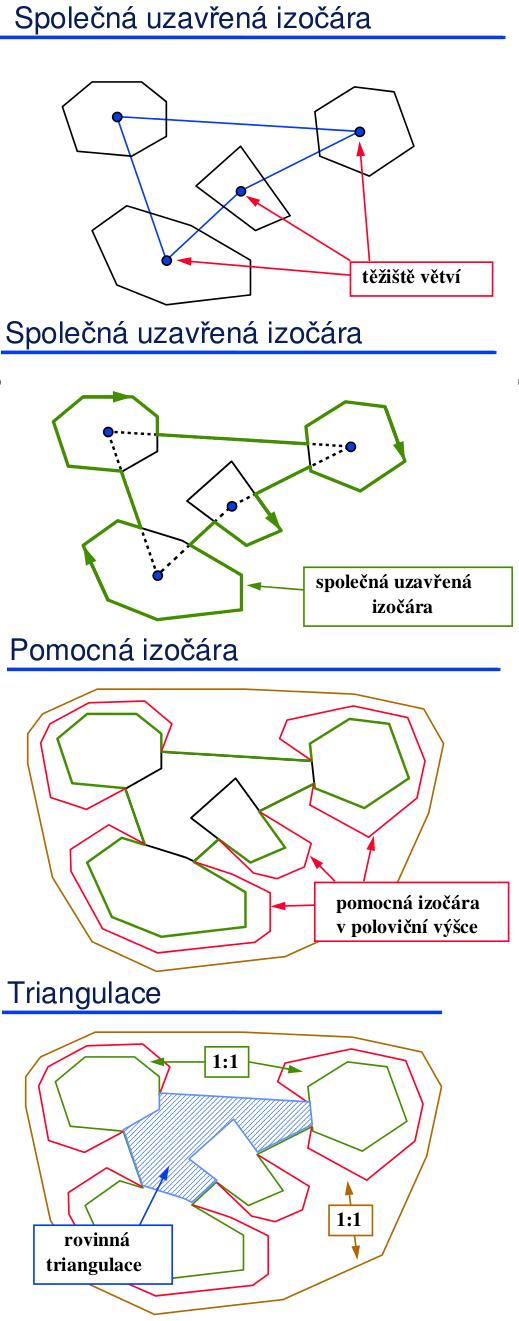
- Větvení 1:N: spočítáme pomocnou izočáru v polovině mezi oběma řezy - konstrukce společné uzavřené izočáry pokrývající všechny spojované větve. Interpoluje se pomocí prvního kroku algoritmu napojování 1:1: N-krát aplikuji napojení 1:1 mezi každou větví a pomocnou izočárou. Doplníme příp. rovinnou triangulaci.
- Přiřazování větví soused. řezů: automatická procedura rozhodující o tom, které větve dvou sousedních řezů se napojí. Jednotlivé komponenty 3D tělesa se mohou v řezech posunovat, měnit tvar nebo rozvětvovat. Předpokládáme dostatečně tenké řezy vylučující variantu větvení M:N. Spojení dvou řezů se zredukuje na několik napojení typu 1:1 a 1:N.
Vlastnosti algoritmu: vstupní izočáry mohou mít libovolné tvary, generuje dobře vypadající trojúhelníky (nepoužívá dlouhé hrany), uspokojivě řeší větvení 1:N, M:N.
Pochodující kostky (“marching cubes”)
Lorensen: 1987. Jeden z nejpoužívanějších algoritmů. Jednoduchá implementace (i HW), generované trojúhelníky nemají dlouhé hrany. Ale může generovat velké množství trojúhelníků (i menších než 1 pixel) mohou se objevit drobné chyby v napojení. Generuje síť trojúhelníků v každé buňce – topologie podle konfigurace vrcholů buňky: vrcholy sítě leží na hranách buňky, snadno se implementuje. Lze použít gradientní stínování.
Konfigurace vrcholů buňky
Základní algoritmus
4 sousední řezy se načtou do paměti. Pro každou buňku mezi dvěma prostředními řezy se spočítá síť: ve všech osmi vrcholech buňky určíme bitovou hodnotu s významem obsahuje / neobsahuje objekt (podle určeného prahu). Tato 8mi bitová informace slouží jako index do předem pevně dané tabulky – informace o vrcholech a hranách trojúhelníků. Vrcholy sítě se spočítají lineární interpolací podle hodnot ve vrcholech buňky. Normálové vektory ve vrcholech buňky se spočítají pomocí diferencí a lineárně se pak interpolují do vrcholů sítě. Síť trojúhelníků se stínováním se zapíše na výstup, předpokládá se HW podpora viditelnosti a Gouraudova stínování.
Implementace, vylepšení
- Spočítané vrcholy sítě a normálové vektory se ukládají do “cache” paměti – v sousedních buňkách se již nemusí počítat.
- Náhrada souvislé sítě trojúhelníků v buňce jediným mnohoúhelníkem (nerovinným), protože průmět buňky je často malý (řádově několik pixelů) – větší efektivita při kreslení.
- Množinové operace, řezy rovinou – paralelně se provádí výpočet několika izoploch.
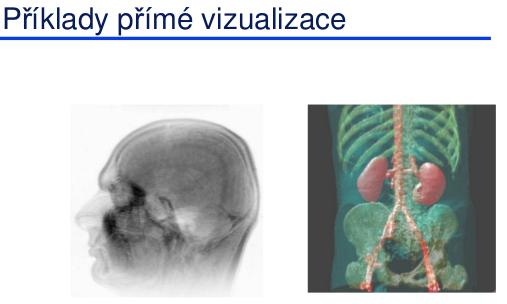
Přímé zobrazování objemových dat
Obrázek může obsahovat více informací, ale je závislý na úhlu pohledu.
V-buffer, “splatting” – konstrukce poloprůhledného zobrazení průchodem scény zepředu dozadu.
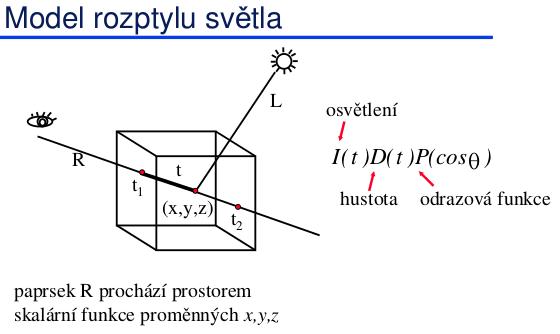
Metody vrhání paprsku
- Simulace rozptylu světla v poloprůhledném (pasivním nebo aktivním) prostředí.
- Integrace podél dráhy paprsku.
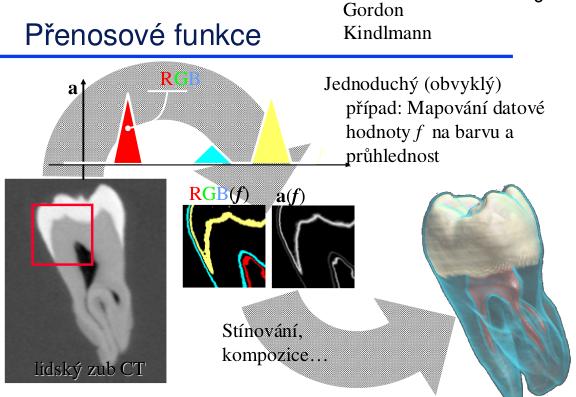
Klasifikace
Originální datová množina obsahuje hodnoty, které jsou specifické pro danou aplikační oblast (teplota, rychlost, hustota protonů, atd.). Datům musíme přiřadit barvy/průhlednosti, které dají datům určitý význam. Řeší se pomocí přenosových funkcí.
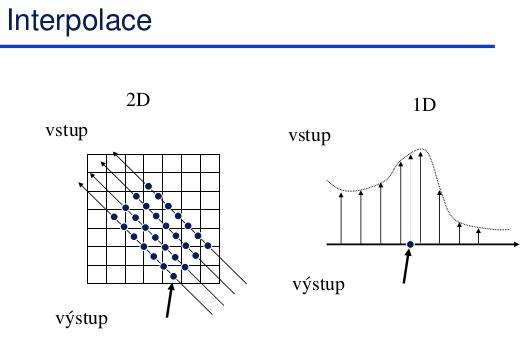
Interpolace v buňkách
- Polynomiální interpolace, aproximace – pro topologicky pravidelné mřížky.
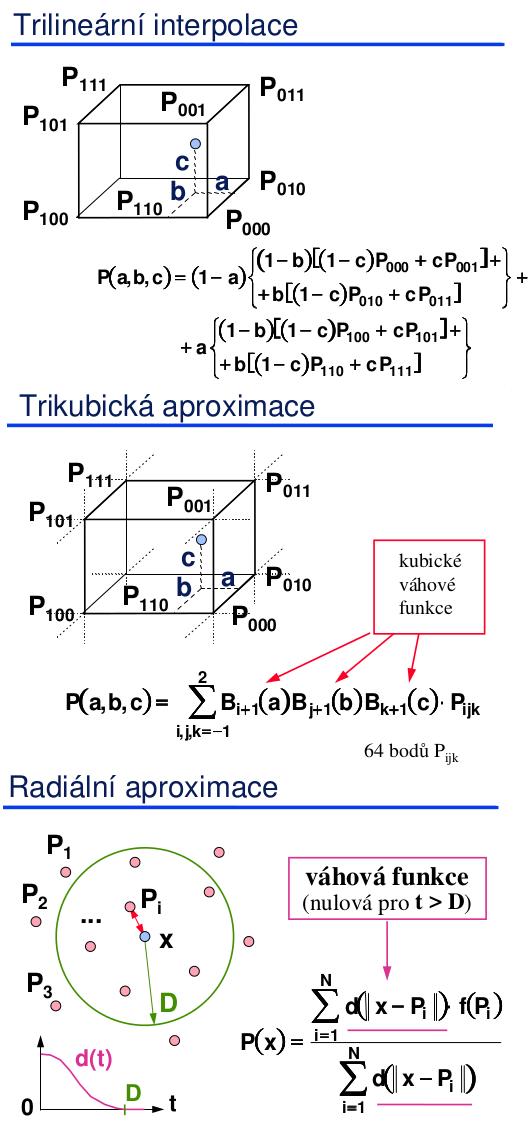
- Trilineární interpolace – jednoduchý výpočet, není hladká.
- Trikvadratická nebo trikubická aproximace – hladké, ale vyžadují topologickou pravidelnost.
- Radiální aproximace – vhodná i pro topologicky nepravidelné mřížky.
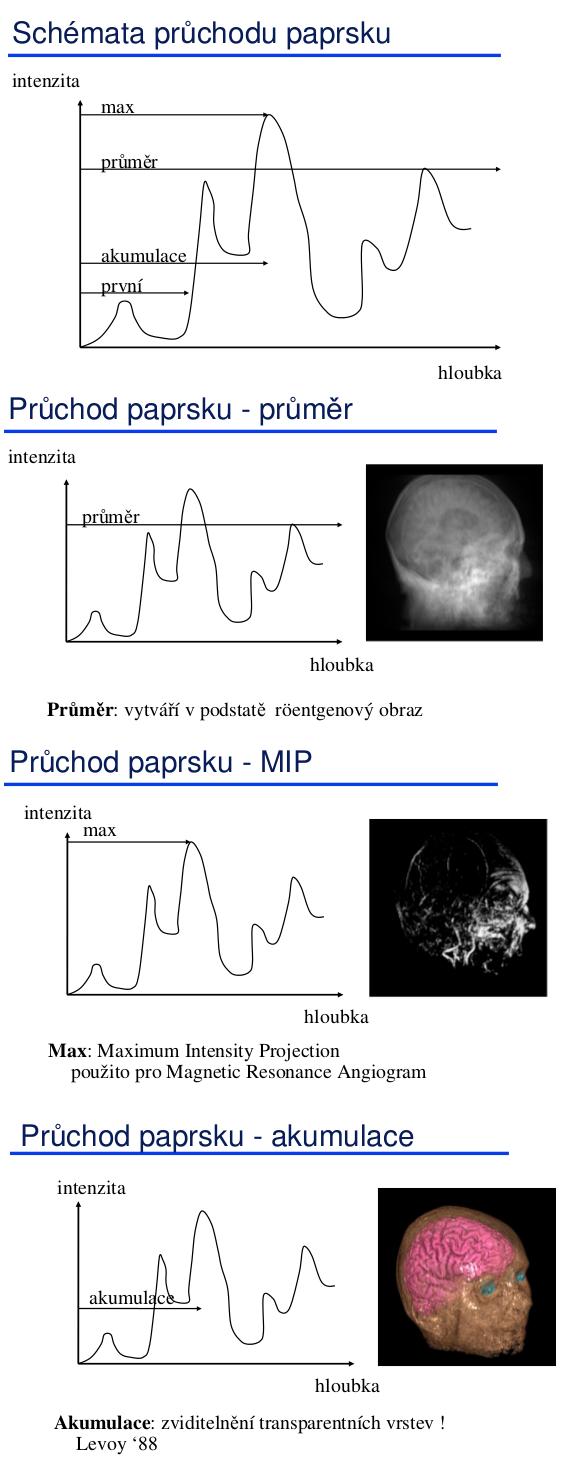
Schémata průchodu paprsku
Typy průchodu
- Průchod daty (scénou) – jednodušší implementace, průmět některých elementů může být zanedbatelný
- Zezadu-dopředu – uživatel si během výpočtu může prohlížet vzdálenější partie datového pole, jednodušší implementace integrálního výpočtu
- Zepředu-dozadu – nemusí být nutné procházet celé datové pole (zadní elementy již nemají vliv na výsledný obrázek), nemusíme počítat celý paprsek (zastavíme se na podprahové hodnotě důležitosti)
- Průchod průmětnou – buňky procházíme mnohokrát (pomalejší výpočet), důležité části vzorkujeme hustě
Fotorealismus
Nemusí být nejdůležitější, hlavní je názornost zobrazení. Člověk je však zvyklý na některé fyzikální vlastnosti látek:
- “Zářící mlha” – poloprůhledná neizotropní látka, která světelné paprsky vyzařuje a zároveň pohlcuje
- Stínování ploch – jednoduchý světelný model; gradientní výpočet N
- Světelné efekty – světlo = ambientní + difúzní + speculární (I = ka Ia + kd Id + ks Is). Obvykle uvažujeme pouze odrazovou složku: světlo = reflexní + absorbované + transmitované.
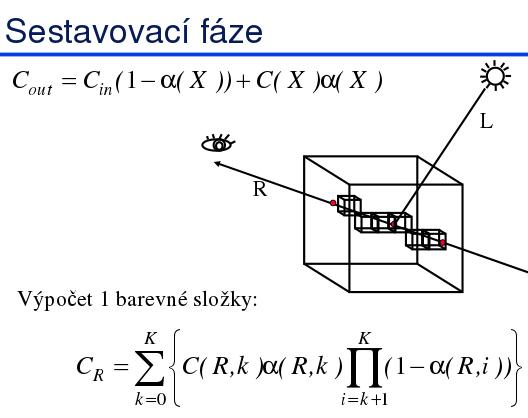
Algoritmus Levoy
Pro ilustraci Předzpracování vytvoří 2 pomocné objemy:
- pomocné pole barev C(X) – pro každý voxel vypočte barvu Phongovým modelem, odhad normály (gradientu) symetrickou diferencí
- pomocné pole neprůhledností α( X ) – klasifikace závislá na aplikaci
Gradientní stínování - výpočet fiktivního normálového vektoru jako gradientu zobrazované funkce. Aproximace gradientu pomocí konečných diferencí
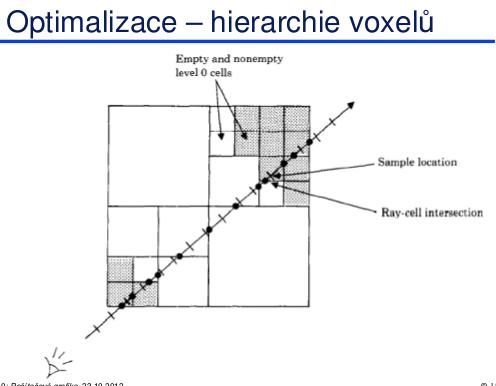
Lze optimalizovat použitím hierarchií voxelů – oktantových stromů – hierarchie obalových objemů pro 8, 64, atd. voxelů.
Použité zdroje
Josef Pelikán, Jiří Sochor : PB009 - Základy počítačové grafiky, slajdy. 2012. Fakulta informatiky, Masarykova Univerzita. Brno.
Josef Pelikán, Jiří Sochor : PA010 - Počítačová grafika, slajdy. 2012. Fakulta informatiky, Masarykova Univerzita. Brno.
Žára, Beneš, Sochor, Felkel. Moderní počítačová grafika. Computer Press, Brno, 2004. ISBN: 80-251-0454-0