Obsah
Zadání
Algoritmy výpočetní geometrie a jejich aplikace při řešení rozsáhlých scén. Aproximace těles. Konvexní obaly, kontrukce ve 2D a 3D. Obalová tělesa, hierarchie obalů, efektivita obalů.
Konvexní obal
Množina bodů K v rovině nebo prostoru (K∈R²,R³) je konvexní, jestliže pro každé 2 body p,q∈K platí, že K obsahuje všechny body úsečky pq. Konvexní obal množiny M je nejmenší konvexní množina obsahující množinu M.
Alg. 1 (Naivní alg.)
Pokud všechny body množiny leží v pravé polorovině určené přímkou pq, pak orientovaná úsečka pq je stranou konvexního obalu (pokud 3 body leží na jedné přímce → nejednoznačnost). Sestrojíme matici D:
(qx-px rx-px)
(qy-py ry-py)
Pokud det(D)>0 pak je bod r vlevo od vektoru q-p, pokud det(D)<0, pak je r vpravo od q-p.
Časová náročnost: O(n³)
Alg. 2 (Inkrementální alg.)
P je množina bodů. Vezmeme bod nejvíce vlevo (p1) a nejvíce vpravo (pn), které rozdělí hranici na horní a dolní konvexní obal. Body P uspořádáme lexikograficky. Body na horním konvexním obalu vždy dělají „zatáčku vpravo“. Předpokládejme, že jsme prošli body p1,p2,…p_i. Chceme přidat p_i+1. Testujeme poslední 3 body konvexního obalu (vč. p_i+1). Jestli tvoří zatáčku vpravo, přidáme do konvexního obalu. Pokud ne, odstraníme prostřední bod a testujeme poslední 3 body obalu… to děláme tak dlouho, až nastane první situace. Dolní konvexní obal sestrojíme analogicky.
Časová náročnost: O(n log n)
Gift Wrapping alg. (Jarvis march in 2D)
Lze aplikovat i v 3D. Postup:
Začínáme nejlevějším bodem p0. Přidáme bod p_i, pokud všechny body množiny leží vpravo od přímky p0p_i. Porovnání: O(n), kde n je počet bodů množiny. Postupujeme s přidáním bodů, dokud nenarazíme na první bod p0.
Časová náročnost: O(k n), k je počet vrcholů konvexního obalu
Divide and Conquer
Lze aplikovat i v 3D. Postup:
- Setřiď body množiny podle x-ových souřadnic, rozděl množinu na dvě poloviny
- Proveď dělení rekurzivně na obou množinách
- Spoj vzniklé 2 konvexní obaly: Najdi nejlevejší bod pravé množiny (p) a nejpravější bod levé množiny (q). Skontroluj, jestli je každý bod pod přímkou pq. Pokud ano, přidej hranu pq do konvexního obalu. Pokud ne, urči horní tečnu (upper tangent) množin, ta bude hranou konvexního obalu. Odstraň nepotřebné hrany z konvexního obalu. Proveď to samé dole → dolní tečna.
QuickHull
- Najdi body s min. (p0) a max. (pn) x-ovou souřadnicí, přidej do konvexního obalu.
- Použi přímku p0pn pro rozdělení množiny bodů na 2 části, každou část zpracuj rekurzivně.
- Urči bod p_i, který leží nejdále od přímky, přidej do konvexního obalu. Body ležící uvnitř trojúhelníku p0-pn-p_i ignoruj.
- Proveď předcházející kroky na nově vzniklých přímkách p0-p_i a pn-p_i, dokud jsou ještě body k dispozici.
Časová náročnost: průměrně O(n log n), v nejhorším případě O(n²) 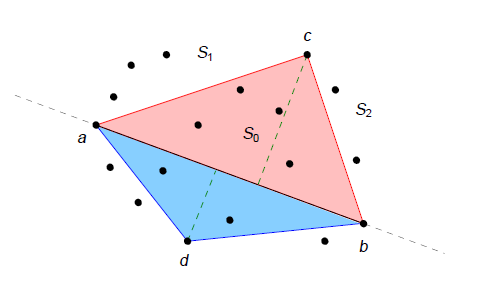
Graham scan
Postup:
- Najdi bod p0 s minimální y-ovou souřadnicí (O(n), n je počet bodů množiny)
- Setřiď body podle úhlu, který zavírá přímka vedená od p0 do daného bodu s osou x (O(n log n))
- Pro každý bod urči, jestli s 2 předcházejícími bodmi, které patří ke konvexnímu obalu tvoří zatáčku doleva nebo doprava. Když se jedná o pravou zatáčku, vyřaď prostřední bod z obalu… Podobně jako alg. 2.
Časová náročnost: O(n log n)
Chan's alg.
Vhodné pro 2D i 3D.
http://en.wikipedia.org/wiki/Chan's_algorithm
Časová náročnost: O(n log h), h je počet bodů konvexního obalu
Obalová tělesa
Jedním z požadavků při zpracování scén a při manipulaci s nimi je určení objektů nacházející se v zadané prostorové oblasti (např. při řešení sledování paprsku, radiositě, detekce kolize). Vhodné uspořádání informací v prostoru výrazně snižuje časové nároky při zpracování scény, ale je nutné zavést pomocné darové struktury (prostorové hierarchie).
Prostorové hierarchie dělíme do dvou kategorií:
- Hierarchie obálek (BVH, Bounding Volume Hierarchies)
- Hierarchie dělení prostoru (Space Subdivision Hierarchies)
 Uvažovaný test (test polohy objektu, test průsečíku objektu s paprskem,…) lze realizovat rychleji s obálkou než se samotným objektem - předběžný, hit/miss test. V případě, že test je true, testuje se objekt.
Uvažovaný test (test polohy objektu, test průsečíku objektu s paprskem,…) lze realizovat rychleji s obálkou než se samotným objektem - předběžný, hit/miss test. V případě, že test je true, testuje se objekt.
Konvexní hraniční obaly
Koule
Nejjednodušší obalové těleso. Invariantní vůči rotaci objektu. Rychlý test protnutí mezi dvěma
sférami (stačí porovnat vzdálenost středů porovnávaných sfér se součtem poloměrů). Nejméně citlivé na tvar tělesa, největší procento obsaženého volného prostoru.  Koule se neprotínají právě když (c1-c2).(c1-c2)>(r1+r2)²
Koule se neprotínají právě když (c1-c2).(c1-c2)>(r1+r2)²
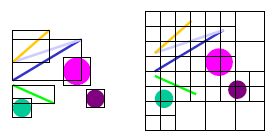
AABB (Axis-Aligned Bounding Boxes)
Osově zarovnaný kvádr. Jednoduchá konstrukce. Stěny kvádru jsou kolmé na souřadnicoví osy, je to min-max obálka všech bodů objektu. V testu překrytí stačí porovnat jednotlivé strany krabice, což je pro
osově orientované krabice velmi jednoduché. Málo citlivé na tvar tělesa. 
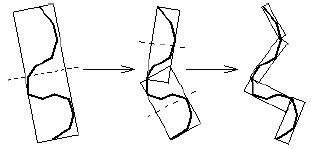
OBB (Oriented Bounding Box)
Orientovaný kvádr, který je orientován tak, aby jeho objem byl co nejmenší. Dobrý obal OBB kopíruje tvar tělesa… ale je obtížnější pro vytvoření. Test kolize 2 obalů je rychlý, stačí provést 15 jednoduchých testů (Dva mnohostěny A a B se neprotínají právě tehdy, pokud existuje separující osa, tj. osa, na kterou se obaly promítnou jako disjunktní intervaly. Počet kandidátů na separující osy pro testování: 2F+E². OBB mají pouze E=3 různé hranové směry a pouze F=3 různé stěnové normály).  Kovarianční matice souřadnic bodů popisuje statistické rozložení (rozprostření) bodů na přímce. OBB je orientován ve směrech největšího a nejmenšího rozložení (které jsou ortogonální).
Kovarianční matice souřadnic bodů popisuje statistické rozložení (rozprostření) bodů na přímce. OBB je orientován ve směrech největšího a nejmenšího rozložení (které jsou ortogonální). 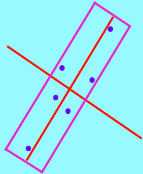 Při nerovnoměrném rozložení bodů vznikne špatný obal. Vylepšení: integrace přes plošky a uniformní navzorkování:
Při nerovnoměrném rozložení bodů vznikne špatný obal. Vylepšení: integrace přes plošky a uniformní navzorkování: 
k-DOP (Discrete Oriented Polytop)
Orientovaný rovnoběžnostěn. Velmi dobře kopíruje tvar tělesa. Průnik několika pásů v prostoru určuje tzv. polytop. Protilehlé roviny obálky jsou rovnoběžné a jejich normály jsou definovány v k diskrétních směrech. V testu se porovnávají vždy pouze rovnoběžné roviny stran sousedících těles. Varianty:
6-dop = kvádr typu AABB
14-dop = kvádr s oseknutými rohy
18-dop = kvádr s oseknutými hranami
24-dop = kvádr s oseknutými rohy a hranami 
Efektivita obalů
Jednoduchá primitiva (koule, AABB, atd.) se dobře vyrovnají s požadavkem na cenu testu. Neposkytují však těsné obalení pro dlouhá štíhlá tělesa. Složitější primitiva (minimální elipsoidy, OBB, atd.) jsou těsnější, ale test překrytí je relativně nákladný. Je nutné vzít v úvahu cenu obnovy BV. 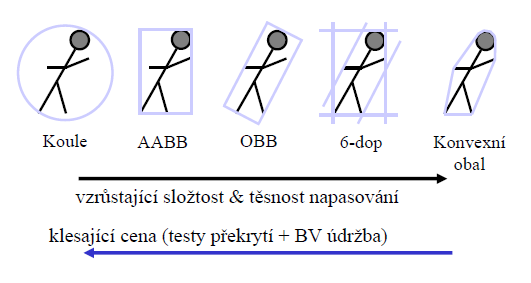
BVH – Bounding Volume Hierarchy
Samotné využívání obálek přináší jen mírné zrychlení výpočtu. K výraznému zrychlení dochází teprve po seskupení obálek do hierarchické stromové struktury (hierarchie obálek). V listech stromu jsou obálky ohraničující individuální objekty scény. Obálky, které leží blízko sebe nebo které se překrývají, se shlukují do větších celků a zapisují se do uzlů na vyšších úrovních stromu. 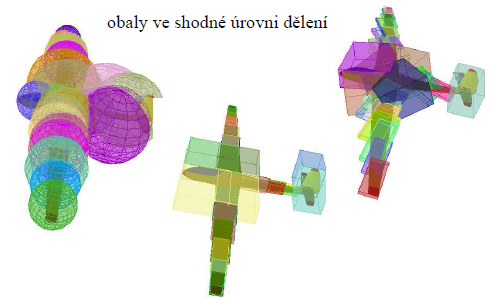 Při úloze zjišťování polohy bodu vzhledem k objektům scény procházíme strom obálek od kořene a testujeme polohu bodu vůči obálce obsažené v uzlu.
Při úloze zjišťování polohy bodu vzhledem k objektům scény procházíme strom obálek od kořene a testujeme polohu bodu vůči obálce obsažené v uzlu. 
Detekce kolize
1. Testuj kolizi mezi dvěma rodičovskými uzly (od kořenů daných stromů)
2. If není překrytí mezi dvěma rodiči,
3. then stop a výsledek “bez kolize”
4. else Všichni potomci jednoho rodičovského uzlu jsou testováni proti všem potomkům druhého rodiče
5. If je kolize mezi potomky
6. then If jsou to listové uzly
7. then nahlaš “kolizi”
8. else jdi na 4
9. else stop a výsledek “bez kolize” 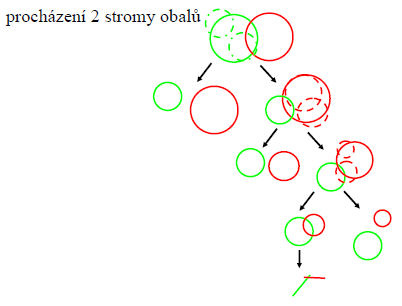
Sférické stromy
Hierarchie množin koulí, které aproximují objekt.
Výhody:
- Jednoduchý test překrytí mezi dvěma obalovými koulemi
- Invariantní vůči rotacím a lze aplikovat stejné transformace na středy obalů, pokud jsou objekty rigidní
Nevýhody:
- Není vždy nejlepší aproximace (zvláště nevhodné pro dlouhé a štíhlé objekty)
- Nedostatek dobrých metod pro tvorbu stromů
k-DOP stromy
Hlavní výzvou je údržba obalů k-dop.
OBB strom
Zdroj
Čadek, M. M7130 - Geometrické algoritmy. 2011. Přírodovědecká fakulta, Masarykova Univerzita, Brno.
Wikipedia, the free encyclopedia.
http://saint-paul.fjfi.cvut.cz/base/public-filesystem/admin-upload/POGR/POGR1/05.vypocetni_geometrie.pdf
Žára, Beneš, Sochor, Felkel. Moderní počítačová grafika. Computer Press, Brno, 2004. ISBN: 80-251-0454-0