mgr-szz:in-tei:14-tei

Obsah

Zadání
Vypracování
Předměty
Diskuze

Zadání

14. Modální a temporální logiky a jejich použití

Vypracování

Problém této otázky ve vztahu ke studiu na FI je, že je rozházena přes více předmětů a v každém se probírá trochu jinak. Navíc jde rozlišit:

teoretickou větev, týkající se především vlastností logik – IA040 Modální a temporální logiky procesů,
praktickou větev, týkající se především LTL, CTL a model checkingu – IV113 Úvod do validace a verifikace.

Tyto předměty (a k nim příslušející materiály) jsou zároveň poměrně dobrým zdrojem ke studiu. Pro účely této otázky se následující text pokouší obsáhnout oba dva přístupy.

Tento text lze více méně použít jako studijní materiál s tím, že pokud potřebujete hlubší pochopení nějakého tématu, je dobré podívat se do materiálů výše uvedených předmětů. LTL a CTL jsou poměrně důležité (v praxi) a proto je taky dobré vědět, jak se od sebe liší.

Motivace

Pokud máme algoritmus, můžeme jeho funkci (nebo význam) popsat pomocí vstupní a výstupní podmínky, které jsou formálně zapsaná jako logická formule. Na jejich základě můžeme zkusit dokázat, že program má danou funkci, tedy že na vstupech splňující vstupní podmínku vždy skončí a jeho výstup bude splňovat podmínku výstupní. Když chceme něco takového udělat pro systém, který obsahuje paralelismus, nebo jeho konání nekončí, klasická (prvořádová) logika nám přestává stačit. Přitom takové systémy mají velký praktický význam – patří mezi ně například operační systémy a komunikační protokoly.

Modální a temporální logiky slouží k formální specifikaci (potenciálně) nekonečného chování systémů. Jde jimi vyjádřit celá řada zajímavých vlastnosti, jako například:

„systém vždy může provést nějakou akci“ (tj. nedostane se do deadlocku),
„za akcí SYN vždy následuje akce ACK“,
„systém se nemůže dostat do chybného stavu“,
„systém se vždy může dostat do počátečního stavu“.

V praxi jsou zajímavé především temporální logiky, protože mají větší vyjadřovací sílu (respektive, modální logiky jsou „zahrnuty“ v CTL), lépe se v nich vyjadřují zajímavé vlastnosti a existuje automatická procedura pro ověření, zda daný model systému splňuje formuli temporální logiky, neboli model checking.

Formální modely

Logické formule se typicky nevztahují k skutečným systémům, ale k jejich modelům. Existují dva základní (a do jisté míry záměnné) formální modely systémů (také můžeme říct jejich stavových systémů). Oba dva jsou složeny ze stavů a přechodů mezi nimi. Rozdíl je pouze v tom, jestli jsou značky na přechodech nebo na stavech.

Labelled Transition System (LTS), neboli Označený přechodový systém

Označený přechodový systém je trojice $(S,L,\to)$ , kde:

$S$ je neprázdná množina stavů,
$L$ je neprázdná množina značek,
a $\to\subseteq S\times L\times S$ je přechodová relace.

Typicky píšeme $s_1\stackrel{a}{\to}s_2$ místo $(s_1,a,s_2)\in\to$ .

Kripkeho struktura (KS)

Kripkeho struktura je čtveřice $(S,\to,L,AP)$ , kde:

$S$ je neprázdná množina stavů,
$\to\subseteq S\times S$ je přechodová relace,
$L:S\to 2^{AP}$ je značkovací funkce,
$AP$ je množina atomických propozic.

Atomické propozice jsou typicky nějaké Boolovské výrazy, tj. můžeme říct, že $A$ platí v $s$ , když $A\in L(s)$ .

Různé zdroje uvádějí tyto definice různě. Například u KS se může vynechat množina atomických propozic. Typické je ještě přidat k definici počáteční stav nebo jejich množinu. Důležité je:

každý přechod LTS je označen značkou,
každý stav KS je označen podmnožinou atomických propozic.

Oba dva modely se mezi sebou dají převádět, ne vždy se ale zachovají množiny stavů. Typicky se setkáváme s převodem KS do LTS¹⁾:

Převod KS do LTS

Nechť $(S,\to,L,AP)$ je Kripkeho struktura. Odpovídá ji označený přechodový systém $(S,2^{AP},\Rightarrow)$ , kde $s_1\stackrel{A}{\Rightarrow}s_2\iff s_1\to s_2\land L(s_2)=A$ .

Tedy označíme přechody vedoucí do každého stavu atomickými propozicemi, kterými je daný stav označen. Počáteční stavy se zachovávají.

V praxi, především co se týče model checkingu, se používají spíše Kripkeho struktury. Z teoretického hlediska jsou zase zajímavé LTS, protože na LTS je definován modální μ-kalkulus (viz níže)²⁾. Z toho důvodu v tomto textu definuju různé logiky různým způsobem – modální na LTS a temporální na KS. Když použijeme výše uvedený převod, snadno získáme sémantiku temporálních logik na LTS.

Důležitá poznámka: Ani jedna struktura nemusí být konečná! Pokud není, je typicky zadaná implicitně, tedy místo přechodové relace máme funkci, která pro každý stav vrací jeho následníky, tj $f(s)=\{s'\in S|s\to s'\}$ (pro KS – pro LTS ještě potřebujeme označení přechodů). Taky pak potřebujeme množinu počátečních stavů, nebo prostě nějaký stav, odkud začít.

Příklady

Mějme nějaký program. Stavy jsou zřejmě dané ohodnocením proměnných a mezi nimi se přechází pomocí příkazů programu (tohle odpovídá small step operační sémantice – viz 12-tei). LTS můžeme vytvořit tak, že každý přechod označíme příkazem, který jej provedl. KS můžeme vytvořit tak, že si vytvoříme nějaké Boolovské výrazy nad proměnnými (jako $x>0$ ) a pokud v daném stavu platí, přidáme jej do jeho označení. Pokud chceme KS převést na LTS, přesunou se tyto výrazy na přechody, ale ztratíme informaci o tom, jaké příkazy provádějí přechody mezi jednotlivými stavy.

Kdybychom chtěli vytvořit implicitní reprezentaci, musíme si ještě do stavu přidat to, na jakém místě programu se nacházíme (abychom věděli, jaké příkazy se můžou provést) a nový stav se vypočítá podle možných příkazů.

Podobně se dá vytvořit stavový systém pro model v CCS (viz 15-tei), kde jednotlivé stavy jsou procesy a přechody mezi nimi jsou označené akcí, kterou provedou.

Obecně platí, že pokud máme nějaký programovací jazyk, model programu je dán jeho small-step operační sémantikou. Pro modální logiky má význam i big-step operační sémantika, ale o tom až níže.

Úvodní přehled

Platnost formulí modálních a temporálních logik se typicky vztahuje ke stavu a popisuje chování, které v daném stavu začíná. Různé logiky to dělají různým způsobem. Zatímco modální logiky se zabývají všemi následníky daného stavu a popisují zda všechny nebo některé splňují danou podmínku, temporální logiky se typicky dívají dále do budoucna a sledují možná chování systému začínající v tomto stavu. Na to, co přesně se tímto chováním myslí, jsou dva základní náhledy:

Chování je jeden běh, tedy nekonečná posloupnost stavů (které jsou svými následníky). Pro daný stav pak sleduju všechny možné běhy začínající v daném stavu. Tímto způsobem se o systémech vyjadřuje lineární temporální logika (LTL).
Chování je nekonečná stromová struktura obsahující všechny následníky, následníky následníků, atd. Tímto způsobem se o systémech vyjadřuje logika větvícího se času (CTL – computational tree logic).

Obě tyto logiky jsou užitečné – ačkoliv některé vlastnosti se dají zapsat pomocí formulí LTL i CTL, pro každou z těchto logik existují vlastnosti, které nejdou zapsat pomocí té druhé. Existuje ještě logika CTL*, která zahrnuje obě tyto logiky.

Modální logiky

Modální logiky se vyjadřují o následnících stavu. Zde si uvedeme Hennessyho-Milnerovu logiku (HML). Její syntax je definována následující abstraktní syntaktickou rovnicí:

Syntax Hennessyho-Milnerovy logiky

$\varphi::= tt \mid Q \mid \neg\varphi \mid \varphi_1\land\varphi_2 \mid [a]\varphi$

$tt$ je vždy pravdivá konstanta,
$Q\in AP$ je atomická propozice,
spojky $\neg$ a $\land$ mají význam z výrokové logiky,
$[a]\varphi$ říká, že pro všechny následníky pod $a$ platí $\varphi$ .

Dále zavedeme trochu syntaktického cukru. Můžeme používat všechny spojky známé z výrokové logiky (negace a konjunkce tvoří úplný systém) a označíme $\langle a\rangle\varphi\equiv \neg[a]\neg\varphi$ , což znamená, že existuje následník pod $a$ a platí v něm $\varphi$ .

Sémantika HML je dána na LTS, takže množina atomický propozic $AP$ je libovolná a nemusí nutně souviset s množinou atomických propozic v KS³⁾. Kromě LTS tedy budeme ještě potřebovat funkci, která udává význam atomických propozic – valuaci.

Modální model

Nechť $T=(S,L,\to)$ je LTS a $\mathcal{V}:AP\to 2^Q$ je valuace. Modální model je dvojice $\mathcal{M}=(T,\mathcal{V})$ .

Samozřejmě, pokud pracujeme s KS, bude nás určitě zajímat valuace, která odpovídá atomickým propozicím platným v jednotlivých stavech. Splněnost formule je dána pro každý stav:

Sémantika HML

$\begin{array}{rcl} s\models_\mathcal{M} tt &&\\ s\models_\mathcal{M}Q &\iff& s\in\mathcal{V}(Q)\\ s\models_\mathcal{M}\neg\varphi &\iff& s\not\models_\mathcal{M}\varphi\\ s\models_\mathcal{M}\varphi_1\land\varphi_2 &\iff& s\models_\mathcal{M}\varphi_1\land s\models_\mathcal{M}\varphi_2\\ s\models_\mathcal{M}[a]\varphi &\iff& \forall s'\in S:s\stackrel{a}{\to}s'\implies s'\models_\mathcal{M}\varphi\\ \end{array}$

Poznámka: Pokud stav $s$ nemá následníka pod $a$ , triviálně $s\models_\mathcal{M}[a]\varphi$ pro libovolnou formuli $\varphi$ .

Splněnost jde rozšířit na model ( $\models_\mathcal{M}\varphi$ nebo $\mathcal{M}\models\varphi$ když je $\varphi$ splněna pro všechny stavy) a pro systém (když je splněna pro všechny valuace).

Příklady

Co lze s pomocí takové logiky vyjádřit?

$\langle a\rangle tt$ – lze provést $a$ .
$[a]\langle b\rangle tt$ – pokud lze provést $a$ , lze pak provést $b$ .

Vlastnosti začínají být zajímavé, když se přesuneme do splněnosti pro daný systém, tedy když atomické propozice můžou označovat libovolnou množinu stavů (i prázdnou):

$\models_T\langle a\rangle Q$ – každý stav má smyčku pod $a$ .
$\models_T\langle a\rangle Q\to[a]Q$ – když v libovolném stavu existuje přechod pod $a$ , je to jediný přechod pod $a$ .
$\models_T\langle a\rangle\langle a\rangle Q\to \langle a\rangle Q$ – přechody pod $a$ určují tranzitivní relaci.

Zajímavé je spojení s big-step operační sémantikou programů (viz 12-tei), kde $s_1\stackrel{p}{\to}s_2$ když provedení programu $p$ ve stavu $s_1$ skončí ve stavu $s_2$ . Pokud $\varphi$ označuje vstupní a $\psi$ výstupní podmínku, určuje formule $\phi\to[p]\psi$ korektnost programu $p$ .

Vlastnosti

HML má úplný axiomatický systém.
HML je rozhodnutelná, tedy je algoritmus, který pro danou formuli rozhodne, zda existuje model, v jehož některém stavu je splněná. To zároveň znamená, že lze o HML formuli rozhodnout, zda je tautologie (tedy že je není splnitelná její negace).
HML model checking, tedy problém jestli daný stav daného konečného modálního modelu splňuje danou formuli, je rozhodnutelný v lineárním čase (pro nekonečné modely neexistuje obecný algoritmus).

Lineární temporální logika (LTL)

LTL je nejznámějším reprezentatem temporálních logik, které se vyjadřují o bězích v Kripkeho struktuře (nebo LTS).

Běh v KS

Běh v KS je maximální (tj. nerozšiřitelná) posloupnost stavů taková, že dva po sobě jdoucí stavy jsou svými následníky v KS.
Pokud má KS iniciální stavy, požaduje se, aby běhy začínaly v iniciálním stavu.

Běh je typicky nekonečný. Může se stát, že běh v některém stavu končí (pokud nemá žádného následníka). Technicky to jde řešit dvěma způsoby (v podstatě ekvivalentními):

Pokud je běh konečný, předpokládá se, že se poslední stav opakuje donekonečna.
Zavede se „sink“ stav („černá díra“), do kterého jdou přechody ze stavů, které nemají žádné následníky a na kterém je smyčka. Typicky v něm neplatí žádné atomické propozice.

Pro naše účely si zavedeme, že $\pi_i$ označuje $i$ tý stav běhu $\pi$ a $\pi^i$ označuje jeho $i$ tý suffix, i.e. $\pi^i=(\pi_i,\pi_{i+1},\ldots)$ .

Syntax a sémantika LTL

$\varphi ::= tt \mid Q \mid \neg\varphi \mid \varphi_1\lor\varphi_2 \mid X\varphi \mid \varphi_1 U\varphi_2$ Kde $tt$ je konstanta „pravda“, $Q$ je atomická propozice.

Nechť $(S,\to,L,AP)$ je KS, $\pi$ je běh na ní. Sémantika LTL je definována:
$\begin{array}{rcl} \pi\models tt&&\\ \pi\models Q &\iff& Q\in L(\pi_i)\\ \pi\models\neg\varphi &\iff& \pi\not\models\varphi\\ \pi\models\varphi_1\lor\varphi_2 &\iff& \pi\models\varphi_1\lor\pi\models\varphi_2\\ \pi\models X\varphi &\iff& \pi^1\models\varphi\\ \pi\models \varphi_1U\varphi_2 &\iff& \exists k:\pi^k\models\varphi_2\,\land\\ &&\forall i\in\{0,\ldots,k-1\}:\pi^i\models\varphi_1\\ \end{array}$

Samozřejmě můžeme využívat libovolné výrokové logické spojky. Operátory $X$ a $U$ se nazývají temporální operátory. Jejich intuitivní význam je následující (zároveň si zavedeme další syntaktické zkratky):

$X\varphi$ – operátor next: $\varphi$ platí v následujícím stavu . Tento operátor se občas také značí jako $O\varphi$ .
$\varphi_1 U\varphi_2$ – operátor until: v nějakém budoucím stavu na běhu platí $\varphi_2$ a do té doby platí $\varphi_1$ .
$F\varphi\equiv tt U\varphi$ – operátor future: v nějakém budoucím stavu platí $\varphi$ . Občas se značí jako $\diamond\varphi$ .
$G\varphi\equiv \neg F\neg\varphi$ – operátor globally: ve všech stavech běhu platí $\varphi$ . Občas se značí jako $\square\varphi$ .
$\varphi_1 R\varphi_2\equiv\neg(\neg\varphi_1 U\neg\varphi_2)\equiv G\varphi_2\lor \varphi_2U(\varphi_1\land\varphi_2)$ – operátor release:
$\varphi_2$ platí pořád a nebo do té doby než platí $\varphi_1$ (obě musí platit současně). Pozor, oproti $U$ jsou formule v opačném pořadí – dobrá mnemotechnická pomůcka je $\varphi_1$ „uvolňuje“ $\varphi_2$ .

Říkáme, že stav splňuje formuli, pokud ji splňují všechny běhy, které v něm začínají. Pokud má formuli splňovat celý systém, musí ji splňovat všechny stavy a nebo všechny počáteční stavy (pokud jsme si je definovali).

LTL na LTS

Výše uvedená definice LTL je praktická, pro účely model checkingu. Na LTS ji můžeme definovat dvěma způsoby:

Podobně jako HML (viz výše), tedy že potřebujeme valuaci, která říká, ve kterých stavech jsou platné jednotlivé atomické propozice. V tom případě nás vůbec nezajímají značky na přechodech.
Zajímají nás značky na přechodech. Pak je běh dán posloupností přechodů (ne stavů), které popřípadě začínají v počátečním stavu a sémantika LTL je podobná:
1. Každý přechod je označen jednou atomickou propozicí – splňuje pouze danou atomickou propozici.
2. Každý přechod je označen podmnožinou atomických propozic – splňuje všechny atomické propozice, které na něm jsou.

Podtřídy LTL

Můžeme definovat i LTL, která nemá všechny temporální operátory. Obecně se tím však snižuje vyjadřovací síla⁴⁾.

LTL která má místo $U$ pouze $F$ (nebo $G$ ) je slabší.
LTL bez $X$ nedokáže od sebe rozpoznat „koktavé“ („stuttering“) běhy, tedy běhy, kde se opakují stavy se stejným označením (nebo stejné stavy). Konkrétně nejde od sebe odlišit například běhy $s_0s_1s_1s_2s_1^\omega$ a $s_0s_1s_2s_2s_1^\omega$ .

Příklady

LTL může vyjádřit poměrně zajímavé vlastnosti. Zde jsou některé, které se používají v praxi (podobným vlastnostem, do kterých je ještě třeba doplnit formuli, se říká „patterns“):

$G\neg \varphi$ – nikdy nenastane $\varphi$ (nedostanu se do nějakého chybného stavu – safety).
$GF\varphi$ – systém se vždy dostane do stavu, kde platí $\varphi$ (liveness).
$G(\varphi\to F\psi)$ – pokud nastane $\varphi$ nutně někdy v budoucnu nastane $\psi$ (response).

Logika výpočetního stromu (CTL)

Zatímco LTL se zabývá jednotlivými běhy, CTL (a podobné, tak zvané branching tj. „větvící se“ logiky) zkoumají stromovou strukturu, která v jistém ohledu obsahuje všechny možné běhy. Pro účely následující definice si zavedeme značení $\Pi_M(s)$ což je množina všech běhů v Kripkeho struktuře $M$ začínající ve stavu $s$ .

Syntax a sémantika CTL

$\varphi::=tt \mid Q \mid \neg\varphi \mid \varphi_1\lor\varphi_2 \mid EX\varphi \mid E[\varphi_1U\varphi_2] \mid A[\varphi_1U\varphi_2]$ Nechť $M=(S,\to,L,AP)$ je KS a $s\in S$ . Sémantika CTL je definována:
$\begin{array}{rcl} tt\models\varphi&&\\ s\models Q&\iff& Q\in L(s)\\ s\models \neg\varphi &\iff& s\not\models\varphi\\ s\models \varphi_1\lor\varphi_2 &\iff& s\models\varphi_1\lor s\models\varphi_2\\ s\models EX\varphi &\iff& \exists s':s\to s'\land s'\models\varphi\\ &\iff& \exists\pi\in \Pi_M(s):\pi_1\models\varphi\\ s\models E[\varphi_1U\varphi_2] &\iff&\exists\pi\in\Pi_M(s):\left(\exists k:\pi_k\models\varphi_2\land\forall i\in\{0,\ldots,k-1\}:\pi_i\models\varphi_1\right)\\ s\models A[\varphi_1U\varphi_2] &\iff&\forall\pi\in\Pi_M(s):\left(\exists k:\pi_k\models\varphi_2\land\forall i\in\{0,\ldots,k-1\}:\pi_i\models\varphi_1\right)\\ \end{array}$

Je zde vidět, že použité operátory jsou podobné jako u LTL, jen v případě $U$ pomocí kvantifikátorů specifikujeme, jestli mají platit pro jeden nebo všechny běhy začínající v daném stavu. Formule $EX\varphi$ vyžaduje, aby v jendom z následníků stavu platilo $\varphi$ , což se velmi podobá tomu, co umožňují modální logiky (pokud se nedíváme na označení přechodů).

Definujeme ještě další syntaktické zkratky, jejichž význam je podobný jako u LTL:

$AX\varphi\equiv\neg EX\neg\varphi$ – ve všech následnících stavu platí $\varphi$
$EF\varphi\equiv E[tt U\varphi]$ , $EG\varphi\equiv\neg EF\neg\varphi$ .
$AF\varphi\equiv A[tt U\varphi]$ , $AG\varphi\equiv\neg AF\neg\varphi$ .

Logika CTL nemusí být úplně nejjednodušší na pochopení, zde je obrázek stavu, jeho následníků a jejich následníků, na kterých jsou ilustrovány jednotlivé operátory, tak aby $s\models\xi$ , kde, zleva doprava $\xi\equiv EX\varphi$ , $\xi\equiv AX\varphi$ , $\xi\equiv E[\psi U\varphi]$ a $\xi\equiv A[\psi U\varphi]$ , přičemž stavy splňující $\varphi$ jsou černé a stavy splňující $\psi$ šedé.

Na LTS můžeme sémantiku CTL definovat analogicky k LTL. Podobné je to také s vyjadřovací silou operátorů.

Příklady

CTL umožňuje nadefinovat podobné vlastnosti jako LTL, i když s několika rozdíly.

$AG\neg\varphi$ – nikdy, tj. pro všechny běhy, nenastane $\varphi$ . Pro srovnání, $EG\neg\varphi$ říká, že existuje běh, ve kterém nikdy nenastane $\varphi$ .
$AGEF\varphi$ – vždy je možné (existuje takový běh), kterým se dostaneme do $\varphi$ .

Vztah LTL a CTL, CTL*

Výše bylo zmíněno, že existují vlastnosti, které se dají vyjádřit pomocí LTL a nedají pomocí LTL a naopak. Co to znamená? Každá formule jednoznačně určuje třídu modelů, což jsou ty modely, které ji splňují. Zřejmě tedy existují třídy modelů, které se dají definovat pomocí LTL, ale ne pomocí CTL (a napopak). Formálně:

Expresivita logik

Logika $\mathcal{L}_1$ má stejnou nebo větší vyjadřovací sílu než logika $\mathcal{L}_2$ , psáno $\mathcal{L}_2\le\mathcal{L}_1$ právě tehdy, když:
$\forall\varphi\in\mathcal{L}_2.\exists\psi\in\mathcal{L}_1.\forall M.(M\models\varphi\iff M\models\psi)$ Logiky mají stejnou vyjadřovací sílu, $\mathcal{L}_1\equiv\mathcal{L}_2$ pokud $\mathcal{L}_1\le\mathcal{L}_2$ a $\mathcal{L}_2\le\mathcal{L}_1$ .

Platí, že $LTL\not\le CTL$ a $CTL\not\le LTL$ . Dokázat takové tvrzení je značně netriviální, už z výše uvedené definice. My si zde ukážeme, že CTL formule $AG(EF (q))$ nemá eqvivalent v LTL.

Vezměme si následující dva systémy s počátečním stavem a dvojicí atomických propozic $p$ a $q$ :
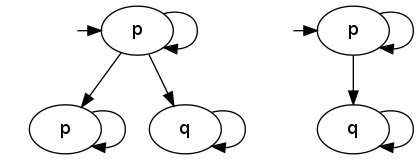Oba systémy produkují stejné běhy z počátečního stavu: $p^\omega+p^*q^\omega$ , z tohoto důvodu nejdou rozlišit pomocí LTL, protože formule LTL se vyjadřují o bězích. Přitom počáteční stav levého systému nesplňuje formuli $AG(EF (q))$ (pokud se dostanu do stavu označeného $p$ vlevo dole, už se nemůžu dostat do stavu označeného $q$ ), zatímco počáteční stav pravého systému ji splňuje. Z toho důvodu $CTL\not\le LTL$ . Je z toho také vidět, že formule $AG(EF (q))$ , která by intuitivně měla vyjadřovat, že se vždy můžu dostat do stavu označeného $q$ , se nechová tak, jak bychom čekali – v pravém systému, který ji zřejmě splňuje, lze provést nekonečný běh $p^\omega$ , kdy se do stavu $q$ vůbec nedostanu. Oproti tomu LTL formule $GF(q)$ není tímto systémem splněna a tím pádem se více blíží vlastnosti „vždy se můžu dostat do stavu $q$ “.

Některé formule mají LTL a CTL společné, například $G(p)$ má stejný význam jako $AG(p)$ . Z toho by se mohlo zdát, že CTL formule vzniknou doplněním áček do CTL formulí. Není tomu ale tak, například formule $FG(p)$ a $AF(AG(p))$ nejsou stejné. To lze ukázat na následujícím modelu (kde „!p“ symbolizuje $\neg p$ ):
Ten produkuje běhy $p^\omega+p^*.(\neg p).p^\omega$ , tedy zřejmě splňuje $FG(p)$ . Podívejme se na platnost formule $AF(AG(p))$ . Nejprve její sémantika. Tato formule požaduje, aby v každém běhu začínajícím v počátečním stavu byl jeden stav, ze kterého se můžeme dostat pouze do stavů, kde platí $p$ . Z počátečního stavu ale vede běh $p^\omega$ , ve kterém zůstáváme v počátečním stavu. Z počátečního stavu je ale dostupný i stav, ve kterém $p$ neplatí a systém nesplňuje $AF(AG(p))$ .

CTL*

Kromě LTL a CTL existuje ještě logika CTL*, která v sobě zahrnuje obě tyto logiky. Funguje tak, že má dva typy formulí – formule cesty a formule stavu:

Formule se vyjadřují o stavech KS a patří mezi ně atomické propozice.
Formule cesty se vyjadřují o bězích na KS a vytvářejí se z formulí stavu nebo formulí cesty pomocí temporálních operátorů.
Formule stavu se dají vytvořit z formulí cesty pomocí kvantifikací pomocí $A$ nebo $E$ , což označuje že platí pro všechny běhy začínající v daném stavu nebo pro alespoň jeden z nich (po řadě).

Syntax CTL*

$\begin{array}{r@{\ ::=\ }l} \varphi & tt \mid Q \mid \neg\varphi \mid \varphi_1\lor\varphi_2 \mid A\psi \mid E\psi\\ \psi & \varphi \mid \neg\psi \mid \psi_1\lor\psi_2 \mid X\psi \mid [\psi_1U\psi_2]\\ \end{array}$

CTL* už je značně komplikovaná logika⁵⁾.

Model Checking

Pravděpodobně nejdůležitější praktické využití temporálních logik je model checking což je automatická verifikační procedura, která pro daný model (KS) a formuli rozhodne, jestli model splňuje formuli.

Poznámka

Tato část se spíše vztahuje k otázce 16-tei, každopádně, model checking vyžaduje zavedení temporálních logik. Proto je uveden zde.

Tento text model-checking popisuje pouze rámcově, protože jinak je to velmi obsáhlá kapitola. Celá procedura jak pro LTL, tak pro CTL je velmi dobře popsána ve studijních materiálech k předmětu IV113 Úvod do validace a verifikace, které jsou dostupné na http://www.fi.muni.cz/~xbarnat/IV113/index.html, konkrétně jde o slidy 06, 07, 08 a 09.

Název „model checking“ zřejmě není příliš český. Lze místo něj sice použít termín „ověřování modelu“, ale v praxi nikdo nebude vědět, o čem je řeč. Proto model checking.

LTL model checking

LTL model checking je úzce spojen s Büchiho automaty. Büchiho automat je v zásadě nedeterministický konečný automat, který ale akceptuje místo konečných slov (pokud jejich čtení končí v akceptujícím stavu) slova nekonečná, a to tehdy, pokud při jejich čtení projde některým z akceptujících stavů nekonečněkrát. Využívá se následující pozorování:

Běhy na jednom modelu (KS) tvoří třídu nekonečných slov – jazyk $L_M$ .
Běhy splňující LTL formuli tvoří třídu nekonečných slov – jazyk $L_\varphi$ .
Pokud $L_M\subseteq L_\varphi$ , nutně $M\models\varphi$ .
Některé třídy nekonečných slov (specificky výše uvedené) se dají akceptovat pomocí Büchiho automatů.
Na Büchiho automatech můžu provádět operace typu průnik a podobně.
$L_M\subseteq L_\varphi\iff L_m\cap \overline{L_\varphi}=\emptyset$ a $\overline{L_\varphi}=L_{\neg\varphi}$ .

Procedura pak funguje následovně:

Vytvoříme Büchiho automat pro $L_M$ . Protože Büchiho automaty mají označené přechody, nejprve převedu KS na LTS (viz výše). Pak stačí přidat akceptující stavy, což jsou všechny.
Vytvoříme Büchiho automat pro $L_{\neg\varphi}$ . Existuje pro to značně komplikovaný algoritmus, který postupně rozbaluje formuli.
Uděláme paralelní synchronní spojení těchto automatů, čímž dostaneme průnik jejich jazyků.
Zjistíme, jestli výsledný Büchiho automat akceptuje nějaké slovo, což je ekvivalentní tomu, jestli jeho graf obsahuje akceptující cyklus dostupný z počátečního stavu.

K poslednímu kroku platí, že všechna akceptující běhy Büchiho automatu nejprve docestují z počátečního stavu do některého z akceptujících stavů a pak se do daného akceptujícího stavu neustále vracejí (vytvářejí „laso“). Typicky se používá algoritmus Nested Depth-First Search (zanořené hledání do hloubky), jehož složitost je lineární k velikosti Büchiho automatu⁶⁾.

Složitost LTL model checkingu (daná velikostí výsledného Büchiho automatu) je v $2^{\mathcal{O}(|\varphi|)}\mathcal{O}(|M|)$ a je v PSPACE (viz 2-tei). Exponenciální složitost vůči velikosti formule je dána tím, že LTL se umí vyjadřovat mnohem stručněji než Büchiho automaty. V praxi ale není problém, protože se většinou používají pouze krátké LTL formule. Co je problém, je velikost modelu, tedy stavového prostoru (viz níže).

Poznámka: Je zřejmé, že kromě LTL je možné specifikovat vlastnosti také Büchiho automaty (v praxi se používají).

CTL model checking

Na rozdíl od LTL model checkingu se CTL model checking provádí přímo na Kripkeho struktuře, a to tak, že se zavádí značkovací funkce $label$ , která pro každý stav určí, které z podformulí $\varphi$ v něm platí. Ta se počítá induktivně podle struktury formule (od atomických propozic).

Zřejmě, pokud vím, ve kterých stavech platí $\varphi$ a $\psi$ je jednoduché určit, kde platí $\neg\varphi$ , $\varphi\lor\psi$ , $EX\varphi$ a podobné. Trochu složitější jsou operátory $A[\varphi U\psi]$ a $E[\varphi U\psi]$ .

Platí, že $A[\varphi U\psi]\equiv\neg(E[\neg\psi U\neg(\varphi\lor\psi)]\lor EG\neg\psi)$ (podobně jako rozepsání operátoru release u LTL). Tímto způsobem se lze zbavit nutnosti prohledávat všechny možné běhy. Pro výpočet hodnoty funkce $label$ se používá následující postup:

Pro $E[\psi U\varphi]$ : Začíná se ve stavech, kde platí $\varphi$ a postupně se prochází všichni předchůdci, kde platí $\psi$ . V těchto stavech platí $E[\psi U\varphi]$ .
Pro $EG\varphi$ : Musí existovat nějaký běh, který se pohybuje pouze ve stavech, kde platí $\varphi$ . Algoritmus vyhledá všechny netriviální silně souvislé komponenty v podgrafu modelu daného stavy, kde platí $\varphi$ a z nich pak cestuje po předchůdcích, ve kterých platí $\varphi$ . Ve všech těchto stavech platí $EG\varphi$ .

Časová složitost CTL model checkingu je v $\mathcal{O}(|\varphi||M|)$ ⁷⁾.

Modální μ-kalkulus

μ-kalkuly (existuje jich více) obohacují logiky o rekurzi, čímž značně zvyšují jejich vyjadřovací sílu. Modální μ-kalkulus je založen na Hennessyho-Milnerově logice, ale díky rekurzi má vyjadřovací sílu temporálních logik – konkrétně pokrývá CTL* a tím i LTL a CTL. Modální μ-kalkulus je zajímavý především z teoretického hlediska – množství tvrzení o temporálních logikách se typicky dokazuje na něm.

Syntax μ-kalkulu

$\varphi::= tt \mid Q \mid Z \mid \neg\varphi \mid \varphi_1\land\varphi_2 \mid [a]\varphi \mid \mu Z.\varphi \mid \nu Z.\varphi$ Kde $Q\in AP$ je atomická propozice a $Z\in var$ je proměnná.

Poznamenejme, že $\nu Z.\varphi$ lze vyjádřit pomocí $\mu Z.\varphi$ , ale pro naše účely si jej zadefinujeme zvlášť. Dále můžeme používat všechny spojky výrokové logiky a $\langle a\rangle\varphi\equiv\neg[a]\neg\varphi$ jako v HML.

Sémantika μ-kalkulu je definována poněkud zvláštním způsobem. Pro daný LTS každá formule definuje množinu stavů, ve kterých je platná. Operátory pak provádějí operace nad nimi.

Sémantika μ-kalkulu

Nechť $T=(S,L,\to)$ je LTS a $\mathcal{V}:(AP \cup var)\to 2^S$ je valuace. Množina stavů splňující formuli pro danou valuaci je definována induktivně:
$\newcommand{\vv}{\mathcal{V}}\begin{array}{r@{\ =\ }l} ||tt||^T_\vv & S\\ ||Q||^T_\vv & \vv(Q)\\ ||Z||^T_\vv & \vv(Z)\\ ||\neg\varphi||^T_\vv & S\setminus\left(||\varphi||^T_\vv\right)\\ ||\varphi_1\land\varphi_2||^T_\vv & ||\varphi_1||^T_\vv\cap ||\varphi_2||^T_\vv\\ ||[a]\varphi||^T_\vv & \{s\in S \mid \forall s'\in S.s\stackrel{a}{\to}s'\implies s'\in||\varphi||^T_\vv\}\\ ||\mu Z.\varphi||^T_\vv & \bigcap\left\{S'\subseteq S \,\middle|\, ||\varphi||^T_{\vv[S'/Z]}\subseteq S'\right\}\\ ||\nu Z.\varphi||^T_\vv & \bigcup\left\{S'\subseteq S \,\middle|\, S'\subseteq||\varphi||^T_{\vv[S'/Z]}\right\}\\ \end{array}$ Kde $\mathcal{V}[S'/Z]$ je označení pro valuaci $\mathcal{V}$ upravenou tak, aby $\mathcal{V}(Z)=S'$ .

Sémantika $[a]\varphi$ odpovídá sémantice tohoto operátoru v HML, jen na množinách stavů. Co znamenají výrazy $\mu Z.\varphi$ a $\nu Z.\varphi$ ? Oba dva označují řešení rekurzívní rovnice $Z=\varphi$ ( $\varphi$ zřejmě obsahuje několik výskytů $Z$ ), pokud $Z$ bereme jako množinu stavů. $\mu Z.\varphi$ přitom označuje nejmenší řešení a $\nu Z.\varphi$ největší (pokud má rovnice pouze jedno řešení, jsou stejné).

Okdud se vzaly dva výše uvedené vzorce? Mějme formuli $\varphi$ , která obsahuje $Z$ . Pokud vezmeme $Z$ jako proměnnou, určuje $\varphi$ funkci $\varphi:2^S\to 2^S$ . Řešení $Z=\varphi(Z)$ je pak jejím pevným bodem. Víme přitom, že podmnožiny $\left(2^S,\subseteq\right)$ je úplný svaz, pro který platí Knasterova-Tarskiho věta, která říká, že pokud je funkce na úplném svazu monotónní, její pevné body tvoří úplný svaz, jehož největší a nejmenší prvky jsou dány právě těmito vzorci ⁸⁾. Valuace je zde použita pouze jako technická pomůcka a je zřejmé, že pokud výskytu $Z$ ve formuli předchází $\mu Z.\varphi$ nebo $\nu Z.\varphi$ , je nám jedno, jaká je hodnota $\mathcal{V}(Z)$ .

To, že $\mu$ označuje nejmenší a $\nu$ největší pevný bod můžeme využít pokud máme konečně-stavový prostor. Pokud chceme vypočítat množinu stavů splňující $\mu Z.\varphi$ , začneme s prázdnou množinou a postupně na ní aplikujeme $\varphi(Z)$ , dokud nedojdeme k pevnému bodu (podle Kleeneho věty). Podobně pro $\nu Z.\varphi$ začneme od množiny všech stavů.

Poznámka: Protože Knusterova-Tarskiho věta platí pouze pro monotónní funkce, je nutné zaručit, aby pro $\mu Z.\varphi$ byla $\varphi(Z)$ monotónní. Problém zde činí negace. Proto se požaduje, aby na syntaktickém stromu byl mezi $\mu Z.\varphi$ a libovolným volným výskytem $Z$ (tj. který není pod jinými operátory $\mu$ nebo $\nu$ ) v $\varphi$ sudý počet negací.

Příklady

Modální μ-kalkulus je mocný nástroj, ale může být poněkud obtížně uchopitelný. Proto jsou zde uvedeny příklady vlastností:

$\mu Z.(\varphi\lor\langle a\rangle Z)$ – existuje cesta pod $a$ do stavu, kde platí $\varphi$ (podobá se operátoru „future“).
$\nu Z.(\varphi\land[a]Z)$ – na všech stavech všech cesty pod $a$ platí $\varphi$ .

Pokud nás nezajímají přechody, používá se modální operátory $\langle-\rangle\varphi$ a $[-]$ , které znamenají „existuje následník“ a „pro všechny následníky“. Tyto operátory jsou jen syntaktické zkratky:
$[-]\varphi\equiv\bigvee_{a\in L}[a]\varphi\quad\quad\langle-\rangle\varphi\equiv\bigwedge_{a\in L}\langle a\rangle\varphi$

Pomocí tohoto zápisu můžeme vyjádřit další vlastnosti:

$\mu Z.(\psi\lor(\varphi\land\langle-\rangle Z))\equiv E[\varphi U\psi]$
$\nu Z.(\mu Y.(\varphi\lor\langle-\rangle Y)\land[-]Z)\equiv AG(EF(\varphi))$
$\mu Z.([a]ff\lor\langle a\rangle\langle a\rangle Z)$ – existuje maximální (konečný) běh pod $a$ sudé délky.

Shrnutí

Modální a temporální logiky slouží k vyjádření vlastností přechodových systémů (a to buď LTS nebo KS). Významné logiky zahrnují:

Hennessyho-Milnerovu modální logiku, která se umí vyjadřovat o následnících daného stavu,
lineární temporální logiku (LTL), která se umí vyjadřovat o všech bězích začínajících v daném stavu,
logiku výpočetního stromu (CTL), která se umí vyjadřovat o výpočetním stromě začínajícím v daném stavu, což je stromová struktura obsahující následníky stavu, jejich následníky a tak dále,
CTL*, která kombinuje přístup LTL a CTL,
modální µ-kalkulus, který vzniká obohacením Hennessyho-Milnerovy logiky o rekurzi a má sílu temporálních logik.

Hennessyho-Milnerova logika a modální µ-kalkulus jsou zajímavé především z teoretického hlediska. V praxi se používá LTL a CTL, pro které existuje model checking, automatická procedura, která o modelu (přechodovém systému) dokáže rozhodnout, jestli splňuje formuli dané logiky.

Předměty

IA040 Modální a temporální logiky procesů – možná až příliš detailní informace, především k modálním logikám (temporálním logikám se věnují i jiné předměty).
IV113 Úvod do validace a verifikace – temporální logiky, LTL a CTL model checking (včetně algoritmu na převod LTL formule na Büchiho automat).
IA011 Sémantiky programovacích jazyků – krátký úvod do LTL model checkingu programů.
IA006 Vybrané kapitoly z teorie automatů – Büchiho automaty, jejich vztah s monadickou logikou druhého řádu (monadic second-order logic).
IA159 Formal Verification Methods – velmi pokročilé: Process rewrite systems, LTL model checking zásobníkových automatů.

¹⁾

Nepamatuju si, že by se v některém z předmětů uvedených na téhle stránce probíral opačný převod – když tak viz http://www.win.tue.nl/~timw/downloads/schoren_seminar.pdf – pozor, převod KS do LTS je tam trochu jinak.

²⁾

Proč dvě tak podobné struktury? Historické důvody. V Americe prý používají spíše KS, v Evropě zase raději LTS.

³⁾

Některé definice HML atomické propozice vynechávají.

⁴⁾

Dokázat, že jsou slabší není moc jednoduché – důkazy jsou uvedené ve slidech z IA040 Modální a temporální logiky procesů.

⁵⁾

Doc. Barnat jednou prohlásil, že informatici rozumí buď LTL, nebo CTL. A CTL* pak nerozumí ani jedni.

⁶⁾

Nested DFS má jednu zásadní nevýhodu, není známo, jestli má paralelní variantu. Na FI se podařilo vyvinout dva paralelní algoritmy pro hledání akceptujících cyklů – MAP a OWCTY, které ale mají větší složitost.

⁷⁾

Výhodou CTL model checkingu je, že lze provádět symbolicky. To znamená, že se výpočet množin stavů, které splňují danou podformuli provádí na binárních rozhodovacích diagramech (binary decision diagrams – BDD). Pro více informací viz slidy k předmětu IV113 Úvod do validace a verifikace.

⁸⁾

Důkaz je například v materiálech k předmětu IA040 Modální a temporální logiky procesů.