Zřejmě není třeba znát takto detailně. Spíše pro ilustraci.

Rozdělení na několik geometricky/topologicky odlišných případů:

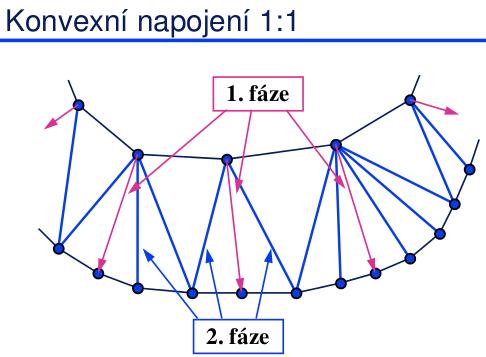
• konvexní napojení 1:1: pro izočáru s menším počtem vrcholů. Každý vrchol se spojí s nejbližším bodem naproti, efektivní algoritmus pracuje inkrementálně - hledá nejbližšího souseda v okolí naposledy přiřazeného vrcholu. Zbývající vrcholy z druhé izočáry se spojí s nejbližšími protějšky. Některé vrcholy se musí spojit se dvěma protějšími body (aby vznikla triangulace).

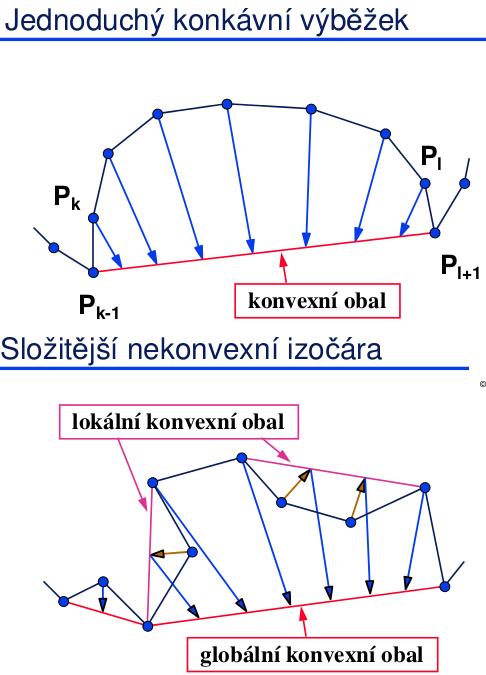
• nekonvexní napojení 1:1: přenášení vrcholů z nekonvexních úseků na konvexní obal izočáry. Hypotéza: konvexní obaly dvou sousedních izočar si budou více podobné. Přenášením se zachovává pořadí i relativní vzdálenosti vrcholů. Triangulace se provádí na konvexních obalech, hranami se potom spojí původní vrcholy izočar.

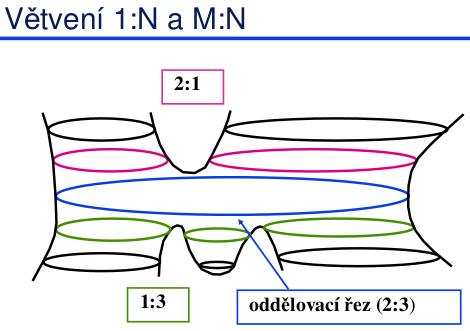
• větvení 1:N a M:N: Hierarchická transformace převádí obecný mnohoúhelník na konvexní. Zachovává počet vrcholů i jejich relativní vzdálenosti. Rekurentní formulace (hierarchický rozklad mnohoúhelníka): transformace lomené čáry Pi, …, Pj - na začátku se bere celý mnohoúhelník P1,…,PN. Výpočet konvexního obalu (i,j) - vrcholy ležící v konvexním obalu se nepřesunují. Pro každou posloupnost vrcholů Pk … Pl (k ⇐ l) neležících v konvexním obalu (i, j) se provedou následující kroky: přenesení vrcholů lomené čáry Pk-1 … Pl+1 do jejího konvexního obalu (k-1, l+1). Rekurentní vyvolání popisovaného algoritmu. Přenesení vrcholů Pk až Pl na úsečku Pk-1 Pl+1, body Pk-1 až Pl+1 již leží v konvexním obalu (i, j), zachování relativních vzdáleností sousedů.

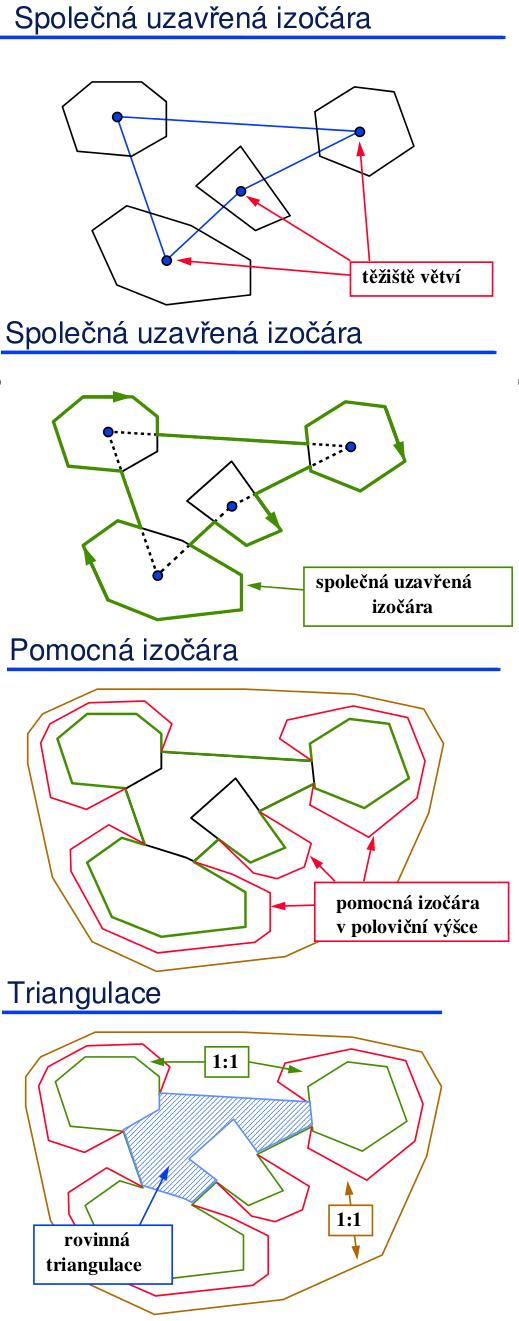
• Větvení 1:N: spočítáme pomocnou izočáru v polovině mezi oběma řezy - konstrukce společné uzavřené izočáry pokrývající všechny spojované větve. Interpoluje se pomocí prvního kroku algoritmu napojování 1:1: N-krát aplikuji napojení 1:1 mezi každou větví a pomocnou izočárou. Doplníme příp. rovinnou triangulaci.

• Přiřazování větví soused. řezů: automatická procedura rozhodující o tom, které větve dvou sousedních řezů se napojí. Jednotlivé komponenty 3D tělesa se mohou v řezech posunovat, měnit tvar nebo rozvětvovat. Předpokládáme dostatečně tenké řezy vylučující variantu větvení M:N. Spojení dvou řezů se zredukuje na několik napojení typu 1:1 a 1:N.

Vlastnosti algoritmu: vstupní izočáry mohou mít libovolné tvary, generuje dobře vypadající trojúhelníky (nepoužívá dlouhé hrany), uspokojivě řeší větvení 1:N, M:N.