Obsah
N-INS 11. Geografické IS
Zadání: Základní principy, pojmy, funkce. Datové modely, DB prostředky, analytické funkce, mapy a standardizace. Metodika vytváření GIS. Typy komerčních systémů.
Nelekejte se prosím, že ta otázka je dlouhá. Je tam hodně obrázků. Radši jsem tam toho dal víc, podle mně je lepší si to přečíst jednou a mít přehled, než se nazpaměť naučit krátký text. Když tak připomínkujte do diskuse. Díky. –Adam
Vymezení pojmu GIS
GIS je jakýkoliv manuálně nebo počítačově založený soubor postupů užívaných k ukládání a manipulování geograficky vztažených dat. Geograficky vztažená data mají dvě složky:
- fyzikální rozměr respektive třídu (průměrná výška stromů v lese, počet obyvatel města, šířka silnice respektive typ sídla, typ vegetace, geomorfologický typ, apod.)
- prostorovou složku, skládá se z
- topologické informace (jde o vtahy mezi objekty, představte si třeba graf z teorie grafů)
- lokalizační informace (vztažení k zemskému povrchu – jaké mají body grafu souřadnice?)
Typy GISů:
- Land Information System (LIS), Land Related Information System (LRIS) – územně orientovaný informační systém - speciální případ GIS v podrobnosti velkého měřítka, který obvykle zahrnuje vlastnické vztahy (hranice parcel a informace o vlastnících parcel)
- Geoinformační systém - systém pracující s daty, která lze lokalizovat v území, ale ne vždy je lze považovat za geografická (umístění vodovodního šoupátka, dopravní značky).
- Prostorový informační systém - systém pracující s daty, která lze lokalizovat v libovolném prostoru. Tento prostor nemusí nutně reprezentovat nějaké území.
- Grafický informační systém - systém pracující s obrazovými daty, která nemá smysl lokalizovat v nějakém (jednotném) prostoru.
GIS jsou navrhovány tak, aby byly schopny reagovat na dotazy typu:
- Kde se nalézá parcela …?
- Jaké typy parcel se nalézají v daném regionu …?
- Jakou výměru parcel vlastní daný oprávněný subjekt?
Historie
Karotgrafie jako obor má zajímavou historii. Geografické informace měli v průběhu staletí cenu zlata a mnohdy byly považovány za státní tajemství, jehož vyzrazení se trestalo smrtí.
Slavné postavy kartografie
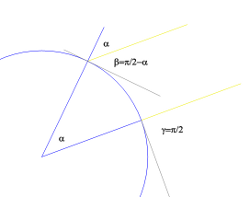
- Erastothénés změřil cca v roce 240 př. Kr. obvod Zěmě. Udělal to změřením úhlů stínů slunečních hodin zároveň na dvou místech starověkého Egypta – Alexandrie a Syéné (dnešní Asuán). Rozdíl úhlů se rovnal úhlu mezi Alexandrií a Syéné, jako dvou bodů na povrchu Země. Spolu se znalostí vzdáleností Alexandrie a Syéné (kruhový oblouk po povrchu Země) a znalostí čísla π, uměl určit obvod celého kruhu zeměkoule.
- Ptolemaios (90 – 160 př. Kr.) – první mapové dílo, kompletní mapa známého světa. Zavedl stupně, minuty, vteřiny. Jeho mapy se používají až do novověku.
- Gerhard Mercator (1512-1594) – vlámský kartograf. Autor Mercatorova zobrazení, které věrně zobrazuje úhly a délky, ale zkresluje plochy. Zobrazení je užitečné při navigaci z místa A do místa B. Loxodromy jsou zobrazeny jako přímky, stačí tedy určit azimut cíle.
Určování polohy
Určování zěměpisné šírky
Určujeme jak daleko jsme od rovníku. Většinou se určovalo pomocí výšky známých souhvězdí a slunce nad obzorem. Pomůcky:
Určování zěměpisné délky
Je potřeba porovnat čas na nultém poledníku a místní čas. Místní čas se zjišťuje čekáním na poledne – periodicky se měří výška slunce nad obzorem a zapisuje čas nultého poledníku. V čase místního poledne je 12:00 hodin a je možné porovnat s časem nultého poledníku. Toto nešlo moc spolehlivě dělat bez přesných hodin, které by ukazovali čas nultého poledníku. Ty byly k dispozici až od 17. století.
Po odměření rozdílu je potřebné udělat korekci (místní poledne se může od středního poledne lišit až o 16 minut). Na to slouží korekční tabulka – analema.
Kartografická zobrazení a mapy
Část věnována základním kartografickým pojmům a principům.
Pojmy
- Geoid (1871 Listing) – Matematické těleso, model povrchu Země. Ekvipotenciální plocha vůči zemské gravitaci, která se nejvíce přimyká ke střední klidové hladině oceánu. Plocha se stejnou úrovní tíhového potenciálu způsobeného gravitací Země.
- Rovina místního poledníku – je rovina určená osou rotace Země a určovaným bodem.
- Zeměpisná délka (λ) – úhel, který svírá rovina místního poledníku procházejícího určovaným bodem a rovina nultého poledníku. Udává se většinou v úhlových jednotkách [-180°, 180°]
- Zeměpisná šířka (φ) – úhel, který svírá rovina rovníku a přímka procházející středem Země a určovaným bodem. Udává se většinou v úhlových jednotkách [-90°, 90°].
- Loxodroma – křivka, která protíná poledníky pod stejným úhlem.
- Ortodroma – nejkratší spojnice dvou bodů, v případě kulového modelu Země kratší oblouk hlavní kružnice.
- Dálkový průzkum Země (DPZ) – získávání informací o zemském povrchu a jeho blízkém okolí pomocí snímacích zařízení (kamery, skenery) umístěných v letadlech nebo družicích
- Topografická mapa – je grafická prezentace (zobrazení) části zemského povrchu se standardizovaným obecným obsahem (voda, lesy, komunikace, objekty viditelné na zemském povrchu, …)
- Tématická mapa – zobrazení geografických dat a jevů v topografickém podkladu pomocí grafické reprezentace prostorových dat: bodů, linií a areálů. Metody reprezentace: bodové značky, lokalizované kartodiagramy, kartodiagramy, symbologie čar, kartogramy.
- Geodetické datum – model zemského tělesa (koule, elipsoid..), jeho umístění (orientace) vůči zemskému tělesu a datum určení.
- Matematická kartografie – disciplína zabývající se převodem zemského povrchu do roviny.
- Geografické souřadnice – určení polohy bodu na ploše elipsoidu pomocí zeměpisné šířky φ a zeměpisné délky λ.
- Geocentrické souřadnice X,Y,Z – prostorový souřadný systém s počátkem ve středu elipsoidu, osa X je vložena do průsečíku rovníku a roviny základního nultého) poledníku, osa Z spojuje střed elipsoidu a severní pól a osa Y leží v rovině rovníku otočena o 90o proti směru hodinových ručiček od osy X.
- Rovinné souřadnice – určení polohy v rovině pomocí dvojice rovinných souřadnic X,Y v ortogonálním souřadném systému. V některých zobrazeních (zobrazení UTM) se používá symbolika E,N (Easting, Northing) tj. rovinné souřadnice narůstající k východu resp. k severu.
- Kartografický souřadný systém – je soubor těchto údajů:
- Geodetické datum (elipsoid, referenční bod, datum určení)
- Souřadný systém geografických souřadnic φ, λ, (včetně volby základního poledníku)
- Zobrazovací rovnice do rovinných souřadnic
- Souřadný systém rovinných souřadnic X,Y
Typy zobrazení
- Konformní zobrazení – ponechává nezkreslené úhly, značně jsou však zde zkreslovány plochy.
- příklad: Mercatorova projekce
- Ekvidistantní zobrazení – nezkresluje délky určité soustavy. Zpravidla touto soustavou bývají zeměpisné poledníky nebo rovnoběžky. Nelze definovat ekvidistantní zobrazení, které bynezkreslovalo žádné délky.
- Ekvivalentní zobrazení – nezkresluje plochy, zkreslení úhlů je však zde poměrně značné, což se projevuje zejména ve tvarech ploch.
- příklad: Petersova projekce
Základní typy převodu geografických do rovinných souřadnic
Nejpoužívanější souřadné systémy v ČR
- Civilní souřadnicový systém S-JTSK je určen – Besselovým elipsoidem z roku 1841 s referenčním bodem Herrmanskogel. Zeměpisné délky se určují od ferrského poledníku.
- Vojenský souřadnicový systém S-42 je určen Krasovského elipsoidem z roku 1942 s referenčním bodem Pulkovo, zeměpisné délky se měří od Greenwiche
- Souřadný systém WGS 84 - Word Geodetic System 1984 – systém byl původně definován Ministerstvem obrany USA pro obranné účely, dnes je celosvětově používanou technologií prostorové lokalizace.
- UTM (Universal Transversal Mercator) – Systém transverzálního válcového zobrazení používající elipsoid WGS 84.
- Cassini-Soldner – Válcové zobrazení na Zachově elipsoidu s referenčními body Sv. Štěpán, resp. Gusterberg. Definováno v Rakousko Uherské monarchii pro stabilní katastr v měřítkách 1:2800 a 1:1440 (dodnes používaná).
- ETRS-LAEA: ETRS89 (Lambert Azimuthal Equal Area) – Elipsoid ETRS89 (téměř shodný s WGS 84), azimutální zobrazení používané pro střední a malá měřítka.
Transformace souřadných systémů
Problém:
Mapy různých kartografických zobrazení transformovat do zobrazení cílového. Základem je znalost, jak transformovat bod.
- Přímá transformace
- Zdrojové souřadnice [x,y] převedeme na geografické souřadnice zdrojového systému [φ, λ].
- [φ, λ] transformujeme do cílových geografických souřadnic [φ', λ' ́]
- Geofrafické souřadnice [φ', λ'] převedeme do cílového rovinného zobrazení [x', y']
- Transformace geografických souřadnic
- Geografické souřadnice [φ, λ] převedeme na geocentrické souřadnice [xs,ys,zs]
- Pro převod mezi dvěma systémy geocentrických souřadnic použijeme tzv. Helmertovu prostorovou transformaci
- Geocentrické souřadnice z 1. převedeme na geografické
- Polynomiální transformace
- Ze znalosti identických bodů ve zdrojovém a cílovém rovinném zobrazení [Xi, Yi] → [Xi', Yi'] určíme koeficienty polynomiální transformace a tuto potom použijeme pro jednotlivé body.
- Používáme polynomy do 3. stupně
- Používá se když:
- není známá zdrojová kartografická projekce prostorových dat
- zdrojová kartografická projekce je známá, ale je zatížená takovou chybou, že obecná polynomiální transformace dává lepší výsledky
- zdrojová projekce je známá, ale její výpočet je příliš náročný
Nalezení koeficientů polynomiální transformace
Výstup: Seznam koeficientů polynomiální transformace zvoleného stupně.
Transformujeme [u, v] do [x, y] s co nejmenší chybou, tedy:
Datové sklady geoinformačních systémů
Prostorové informace je možné ukládat různým způsobem. Tato část představuje základní formáty, které jsou pro tento účel používány.
Rastrová data
Využívají se běžné formáty obrazových dat (bmp, png, jpeg, tif, gif, ecw…). Některé z nich mohou mít informace o vztahu k souřadnicím kartografické projekce přímo ve své hlavičce (ecw, tif) u ostatních se používá „doplňující“ textový soubor (*.TFW), který obsahuje parametry lineárního převodu z/do pixelových do/z kartografických souřadnic.
Typy rastrových dat:
- binární
- polotónová
- víceúrovňová
Sousední pixely
| N | P | N |
| P | X | P |
| N | P | N |
Pixely P jsou přímí (d-) sousedé pixelu X. Pixely N jsou nepřímí sousedé pixelu X.
Kvantitativní charakteristiky obrazu
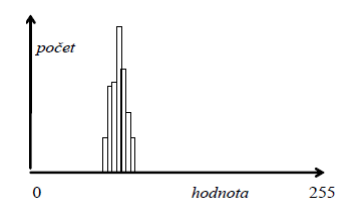
Histogram obrazu
Matice sousednosti
Matice sousednosti je M⨉M matice CM, kde M je počet různých barev obrázku. V buňce [i, j] matice je počet přímo sousedících pixelů o bravě i a j.
Operace nad obrazy
Filtry
Filtry jsou funkce, které počítají hodnotu pixelu z jeho okolí.
Původní obraz:  Zhlazovací filtr:
Zhlazovací filtr:  Zostřující filtr:
Zostřující filtr:  Detektor hran:
Detektor hran: 
Skelet
..... ..... .*.*.. ..*.. ..*.*.. ..*.. ..*..*.. ..*.. ..*...*.. ..*.. ..*....*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*.. ..*....*.. ..*.. ..*...*.. ..*.. ..*..*.. ..*.. ..*.*.. .*.*. ..*.*. ..... .....
Definice:
Nechť R je množina pixelů, B její hranice (kontura), P bod v R. Nejbližší soused bodu P na hranici B je bod M z B takový, že pro každý bod M ́ z B je vzdálenost PM ́ větší nebo rovna vzdálenosti PM. Má-li bod P více než jednoho nejbližšího souseda, nazývá se bodem skeletu množiny R. Sjednocení všech bodů skeletu tvoří skelet množiny R.
Algoritmus – Určení skeletu:
- Urči hranici (konturu) B(R) množiny R.
- Urči množinu násobných pixelů M(R) v hranici B(R)
- Je-li B(R) = M(R), skonči.
- Polož R = R - (B(R) - M(R)) a pokračuj krokem 1.
Vektorová data
Nejdůležitější vektorové formáty
Shape file
- jeden z prvních formátů
- nebosahuje symbolologii (barva, styl linií, výplň polygonu)
- neobsahuje strukturu pro kolekci geometrií
- soubory:
*.shp– prostorová informace*.shx– prostorový index*.dbf– popisná informace a topologické vazby
DGN file, norma IGDS (Intergraph, Bentley)
- bohatý repertoár geometrických primitiv
- soubory:
*.dgn– obsahuje geometrickou informaci*.dfb– obsahuje popis geometrického objektu
Oracle 8x
- uloženo v relační databázi – datový typ
SDO_GEOMETRY
OGC Well known binary
- vytvořeno Open Geospatial Consortiem
- norma binárního ukládání vektorové geometrie (např. struktury jazyka C)
- neobsahuje symbolologii – nestačí samotné pro vykreslení mapy
Point { double x; double y; }; WKBPoint { byte byteOrder; uint32 wkbType; Point point; }; WKBLineString { byte byteOrder; uint32 wkbType; uint32 numPoints; Point points[numPoints]; };
atd.
GML – Geographic Markup Language
- vytvořeno OGS
- norma WKB v XML formátu
- nevhodný pro ukládání, kvůli své velikosti (až 10⨉ větší než u binárních dat), vhodný pro datové přenosy
<CP:geometry> <gml:Polygon srsName="urn:ogc:def:crs:EPSG::2065" gml:id="Polygon_1828023805"> ̈ <gml:exterior> <gml:LinearRing> <gml:posList srsDimension="2"> 541484.77 1113662.92 541484.36 1113666.36 541476.26 1113665.3 541469.89 1113664.51 1113659.06 541469.46 1113660.94 541484.77 1113662.92 </gml:posList> </gml:LinearRing> </gml:exterior> </gml:Polygon> </CP:geometry>
Efektivni přístup k prostorovým datům
Dejme tomu, že máme geografické objekty uložené v relační databázi jako vektorová data. Pokud nechceme při získávání dat z této databáze lineárně procházet všechny záznamy, je potřeba nad nimi vybudovat index, stejně, jako nad jinými typy dat. Tato sekce pojednává o různých typech indexů, pomocí kterých se dá k prosotorovým datům efektivně přistupovat.
Rozsahový dotaz na obdélníky ve 2D prostoru
Vyhledávací množina je konečná množina obdélníků ve 2D prostoru jejichž strany jsou rovnoběžné s osami souřadného systému. Dotazem je libovolný obdélník ve 2D prostoru jehož strany jsou rovnoběžné s osami souřadného systému.
Vyhledávací funkce vrací takové obdélníky, které incidují (mají neprázdný průnik) s obdélníkem dotazu. Taková funkce řeší problém rozsahového dotazu na obdélnících 2D prostoru.
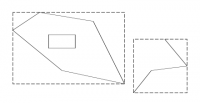
Jednotný zdroj pro prostorovou indexaci geometrických objektů: (tj. struktur pro efektivní vyhledání) je minimální omezující obdélník geometrického objektu rovnoběžný s osami souřadného systému – MBR (minimal bounding rectangle):
tedy minima, resp. maxima lomových (definičních) bodů [xmin, ymin, xmax, ymax]
V naprosté většině případů vystačíme s obdélníkovým dotazem:
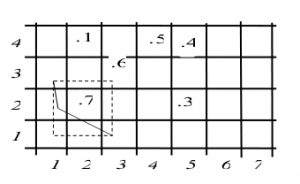
Metoda GRID
Spočívá v rozdělení 2D prostoru na obdélníkovou síť. Elementy sítě lze maticově indexovat, tím prostor „linearizovat“ a využít je tím pro primární prostorový filtr.
+/- metody GRID
+ snadné rozšíření na více dimenzí
+ relativně snadná (resp. řešitelná implementace neobdélníkových dotazů)
- netriviální odhad velikosti GRIDových čtverců, špatná volba má dramatické důsledky
- nepravidelné chování při řádově rozdílné velikosti geometrických objektů
k-D stromy
k-D strom je založen na klasickém binárním vyhledávacím stromu, pro který platí, že pro každý uzel daného stromu jsou:
hodnoty v levém podstromu uzlu ≤ hodnota v uzlu ≤ hodnoty v pravém podstromu uzlu
k-D strom je strom, kde v uzlech je k-tice a kde dva uzly porovnáváme podle i-tého čísla k-tice, kde i je úroveň uzlu (počet uzlů od vrcholu). Tj. srovnávací kritérium se mění na různích úrovních stromu.
kde
Území se takto na každé úrovni stromu rozdělí na poloviny podle jiného kritéria (jiné osi).
Aplikací jsou 2-D stromy, kde lze v uzlech uložit 2D souřadnice bodů a 4-D stromy, kde lze v uzlech ukládat obdélníky.
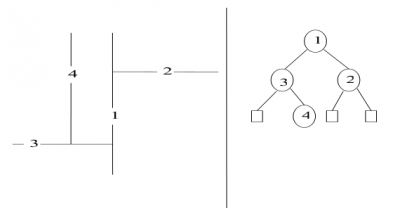
Quad Tree – Kvadrantové stromy
Kvadrantové stromy jsou prostorové vyhledávací struktury založené na pravidelném dělení části 2D prostoru (většinou čtverce) na čtyři stejné části. V základní verzi mohou přímo definovat polygonální geometrii.
Uzel kvadrantového stromu obsahuje položku content, která je buď empty, nebo full a pokud není listem, má také 4 synovské uzly TL, TR, BL, BR (top/bottom left/right).
+/- kvartérních stromů
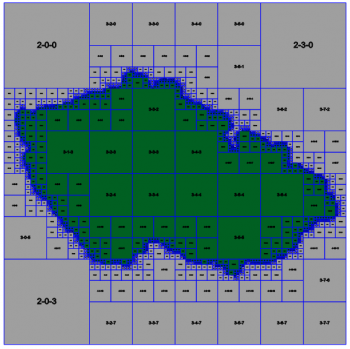
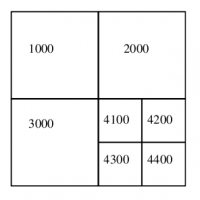
Pevný kvartérní strom (non-pointer Quad Tree)
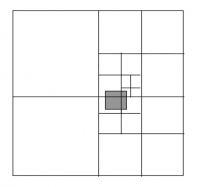
Namísto stromové struktury s pointery na synovské obdélníky je obdélníkům přidělován prefixový klíč.
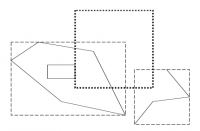
Problematické dotazové obdélníky jsou ty, které procházejí středem území. To pak musíme prohledávat všechno. Toto můžeme obejít rozdělením takového dotazu.
+/- pevných kvartérních stromů
+ „jeden objekt“ = „jeden klíč“, znamená, že prostorová indexace je zabezpečena přímo v geometrické tabulce. Prostorový výběr nevyžaduje součin, či spojení s dalšími tabulkami.
+ každý čtvereční metr Země má konzistentní 21 cifernou adresu
+ z délky adresy lze automaticky odvodit rozlišení 1)
SB+ stromy
SB+ stromy vycházejí z B+ stromů. Ty už bychom měli znát ![]() Pokud jste jako já a potřebujete osvěžit paměť, tak wikipedia:
Pokud jste jako já a potřebujete osvěžit paměť, tak wikipedia:
http://cs.wikipedia.org/wiki/B%2B_strom
http://en.wikipedia.org/wiki/B%2B_tree
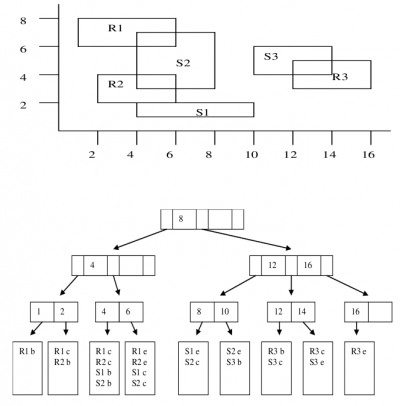
SB+ strom je B+ strom, který v listech uchovává informaci o intervalech, které listem procházejí (resp. v začínají, nebo končí). Pro každou dimenzi existuje jeden SB+ strom 2). Tyto intervaly určují MBR obdélníky geometrických objektů.
Vyhledávání: Máme dotazový interval [xmin, xmax]. Najdeme všchny uzly, které spadají do tohoto intervalu (je to stále B+ strom, takže toto vyhledávání má logaritmickou časovou složitost). Pak jen předej na výstup obsah listů. To samé pro druhou dimenzi. Výsledek je průnik výsledků vyhledání pro jednotlivé dimenze.
Vkládání probíhá jak pro B+ strom: V případě vytváření nového uzlu po štěpení (ve stávajícím uzlu už nebylo místo) je potřeba kromě vkládáného intervalu taky skopírovat hodnotu „prochází“ (na obrázku 'c') pro intervaly, které novým uzlem procházejí. Tj. pokud je nalevo od nového uzlu 'R1b' (R1 začíná), nebo 'R1c' (R1 prochází), tak do nového uzlu dáme 'R1c' (R1 prochází). Pokud je napravo od nového uzlu 'R1e' (R1 končí), nebo 'R1c' (R1 prochází), tak do nového uzlu dáme 'R1c' (R1 prochází).
+/- SB+ stromů
R stromy
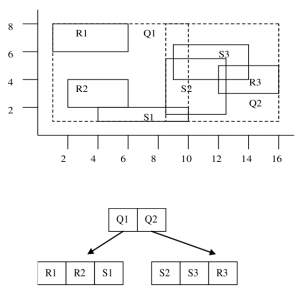
Základní myšlenka: Nad geometrickými objekty, které jsou blízko sebe vybudujeme v struktuře stromu společné předky. R stromy jsou také odvozené z B stromů. Klíče jsou obdélníky.
Vyhledání: Postupuj od vrcholu stromu a pokračuj s těmi syny, se kterými je dotazový obdélník incidentní. Pokud jsme na listu, pošli na výstup incidentní klíče.
Vkládání (mbr nějakého polygonu): Podobně jako v B(+) stromu. Jediná „zapeklitá“ část je rozdělení listu pokud je již plný. Musím rozdělit obdélníky do dvou skupin, ze kterých vybudujeme dva nové uzly. Je při něm potřeba vyřešit následující problém:
Najdi dva obdélníky (možná incidentní) s následujícími vlastnostmi (NP-úplný problém):
- Sjednocení obou obdélníků je původní obdélník
- Oba obdélníky obsahují zhruba stejný počet klíčů
- Oba obdélníky se překrývají co nejméně
+/- R stromy
Funkce a operace nad geometrickými objekty
Prostorovými informace, zejména ty, uložené ve vektorových formátech, lze různě matematicky upravovat a pomocí matematických operací z nich získávat další informace.
Plocha areálu
Vzorec pro výpočet plochy všeobecného polygonu s vrcholy [x1, y1] až [xn, yn] je:
Zdroj:
Myšlenka je postavena na přičítání a odčítání ploch lichoběžníků a funguje pro jakýkoliv polygon. Opravdu dobře vysvětlené to je zde:
Určení orientace polygonu
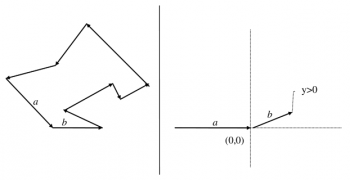
Algoritmus:
- Vyber z hranic oblastí takovou hranici a tři po sobě jdoucí její body tak, aby střední bod měl minimální souřadnici y (ze všech souřadnic y v polygonu) a první bod měl souřadnici y větší, než bod prostřední.
- Rotuj souřadnou soustavu tak, aby orientovaná úsečka definovaná prvními dvěma body splynula s osou x v kladném směru.
- Znaménko souřadnice y posledního bodu určuje orientaci polygonu.
Poloha bodu vůči polygonu
Viz třeba na wikipedii:
Konvexní polygon
Konvexní polygon je polygon s touto vlastností: Každý vnitřní bod úsečky, jejíž krajní body leží na hranici polygonu, je i vnitřním bodem polygonu.
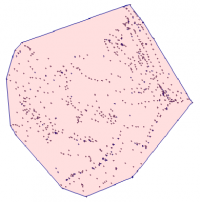
Algoritmus pro vytvoření konvexního obalu (Graham scan):
- Vstup: Množina bodů
- Vyber bod P0 s minimální
ysouřadnicí, pokud je jich víc s minimální, vyber ten nejvíc vpravo (max.xsouřadnice) - Setřiď body vzestupně podle úhlu, který svírá osa
Xs úsečkou mezi body P0 a řazeným bodem - Postupně kreslíme polygon – spájíme body podle seřazení
- Při připojování nového bodu se musíme podívat, jestli nejnovější úsečka
- leží napravo nebo nalevo od předposlední úsečky. Pokud nalevo, ok,
- pokračujeme s dalším bodem. Pokud napravo, pak předposlední připojený bod odpojíme, ten není součástí konvexního polygonu a uděláme novou úsečku z předpředposledního do posledního bodu (na obrázku odpojujeme bod
Ca kreslíme úsečku zBdoD). - Po vrácení se do bodu P0 máme konvexní polygon
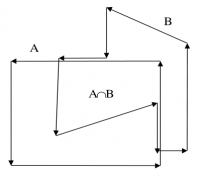
Průnik dvou oblastí
Algoritmus:
- Vstup: dvě orientované oblasti.
- Všechny hrany hranic oblastí modifikuj tak, aby se vzájemně neprotínaly, mohou však splývat s hranami hranic z druhé oblasti. Potom mají tyto vlastnosti
- hrana splývá s jinou z druhé oblasti
- hrana leží celá uvnitř druhé oblasti
- hrana leží celá vně oblasti
- Do seznamu zařaď ty hrany, které buď, leží celé v druhé oblasti, nebo splývají s nějakou hranou z druhé oblasti, se kterou mají stejnou orientaci, (totožné hrany jen jednou).
- Z vybudovaného seznamu zřetěz hranice výsledné oblasti a výsledek pošli na výstup.
Datové modely
Základními modely prostorové složky geografických dat jsou rastrové a vektorové modely.
Rastrový model
Rastrový model dělí modelovanou oblast (WOI) do pravoúhlé sítě buněk, každá buňka obsahuje jednotlivou hodnotu sledovaného údaje. Buňce odpovídá plocha sledované oblasti (území). Jedna množina buněk spolu s asociovanými hodnotami vytváří vrstvu. V databázi může být uloženo mnoho vrstev.
Výhody:
- jednoduchá datová struktura - snadné provádění některých operací - například mezi překrývajícími se vrstvami (overlay)
- zachycuje data s proměnlivou prostorovou složkou (barevný digitální obraz)
- nemusí být žádná primární znalost jevu pro získání dat, vzorkování lze provést automaticky
Nevýhody:
- málo kompaktní (řídké matice)
- obtížná reprezentace topologických vlastností
- neestetický výstup reprezentovaných dat (pouze za cenu zvýšení hustoty dat)
- nemožnost libovolného zvětšování obrazu
Data v rastrovém modelu
Hodnoty uchované v buňce (pixelu)
- hodnota uchovaná v buňce (pixelu) závisí jednak na kódované realitě, jednak na vlastnostech SW
- možnosti: celá čísla, čísla v pohyblivé čárce, alfanumerické hodnoty
- každá buňka - pixel - má pouze jednu hodnotu, což nepřesně interpretuje realitu (hranice jevu prochází buňkou), některé systémy umožňují uchovat více hodnot v jedné buňce a jejich podíly
- rastrová data mohou být vizualizována jako množina mapových vrstev (mapová vrstva je množina dat popisující jednoduchou charakteristiku pro každou buňku uvnitř sledované oblasti)
- typické rastrové databáze obsahují více než sto vrstev, důležitou charakteristikou vrstvy je rozlišení (rozměr buňky), orientace (azimut, úhel mezi severem a směrem sloupců rastru)
Vektorový model
Vektorový model využívá pro vymezení lokalizace diskrétní bodové nebo liniové elementy – úsečky. Diskrétní objekty vektorového datového modelu vznikají spojením úseček. Na rozdíl od rastrového datového modelu nemusí vektorový datový model pokrývat celé území. (Rastrový model říká co se vyskytuje kdekoliv – v každém místě oblasti, vektorový model říká, kde se cokoliv vyskytuje, zobrazuje umístění každého objektu.)
Výhody:
- kompaktní datová struktura
- výhodné uchování topologických vlastností
- blíží se ručně kresleným mapám, možnost estetického výstupu dat
Nevýhody:
- složitější datová struktura
- obtížnější overlay operace
- nevýhodná reprezentace dat s proměnlivou prostorovou složkou (digitální obraz)
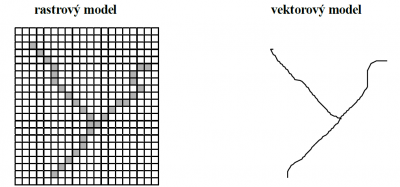
V obou modelech je prostorová informace reprezentována základními (homogenními) jednotkami. V rastrových modelech jsou to pixely (buňky), ve vektorových modelech jsou homogenními jednotkami body, lomené čáry a polygony. Pokud rastrový a vektorový model popisují shodné území ve srovnatelné přesnosti, je v rastrovém modelu řádově více základních jednotek než ve vektorovém modelu. Rozměr základních jednotek v rastrovém modelu je konstantní, rozměr základních jednotek ve vektorových modelech je velice proměnlivý – lomená čára se může skládat ze dvou bodů nebo také z několika desítek tisíc bodů.
Data ve vektorovém modelu
Data je možné vektorom modele uchovávať 3 rôznymi spôsobmi.
Špagetový (spaghetti)) model prostorových dat
Ve špagetovém modelu jsou všechny typy objektů uloženy v jednom heterogenním seznamu. Tento seznam má pouze 2 položky:
- typ objektu – bod, čára, polygon
- parametry objektu – jedna či více souřadnic
Ve špagetovém modelu není obsažena žádná informace o topologii (sousednost, orientace, konektivita, obsahování). Výtahy mezi prostorovými daty musí být odvozeny výpočtem. Výhodou špagetového modelu je levná údržba prostorových dat. Tento model je vhodný pro počítačovou reprodukci map, ale i pro uchovávání prostorových dat, se kterými nebudou prováděny prostorové operace a které mají charakter pozadí – podkladu pro práci s jinými prostorovými daty.
Hierarchický model
Vychádza z faktu, že polygón sa skladá z niekoľkých línií, tie z úsečiek a tie spájajú body.
Táto hierarchická štruktúra je zachovaná pri ukladaní dát.
Topologický model
Topologický model je kompromisem mezi 1. a 2. (uchováva jenom body a čáry, čáry můžou být orientované). Je nejrozšířenějším modelem, který uchovává prostorová data a vztahy mezi nimi. Tímto modelem lze reprezentovat areály i sítě. Základními objekty v tomto modelu jsou:
- rovinný graf (arc – node model)
- areálový rovinný graf
- síťový graf s identifikovanými hranami
- síťový graf s identifikovanými uzly
Topologický model obsahuje topologické objekty, nemusí však obsahovat geometrické objekty (v tomto málo častém případě probíhá údržba prostorových dat bez jejich grafického vyjádření).
Mezi hlavní výhody topologického modelu je možnost provádět analýzy prostorových dat bez užití souřadnic – bez práce s geometrickými objekty. Nevýhodou je nutnost údržby topologické struktury, která se často – zejména pro grafy s velkým počtem prvků – provádí dávkově.
Analytické funkce
Základní členění analytických funkcí:
- údržba a analýza prostorových dat
- údržba a analýza popisných dat
- integrovaná analýza prostorových a popisných dat
Údržba a analýza prostorových dat
Funkce údržby a analýzy prostorových dat jsou ty funkce, které se týkají pouze prostorové složky geografických dat, popisná složka se nemění. K funkcím této kategorie patří:
- transformace formátu prostorových dat (konverze různých typů formátů prostorových dat za účelem přípravy vhodných dat pro další zpracování)
- geometrické transformace (lineární transformace, kvadratická transformace)
- transformace mezi kartografickými systémy (Cassini Soldner - S-JTSK)
- ztotožnění objektů na různých vrstvách systému (nalezení shodných objektů na několika vrstvách - tato situace může být způsobena například několikanásobnou grafickou reprezentací jednoho objektu na vstupu dat)
- ztotožnění objektů na hranicích mapových listů (slouží k propojování objektů, pokud jsou digitalizovány z mapových listů)
- editování grafických objektů (úprava průběhu a polohy prostorových dat)
- zjednodušování průběhu prostorových dat - geometrická generalizace (zmenšení počtu vrcholů lomené čáry, odstranění šumu v naskenovaných rastrových datech)
Údržba a analýza popisných dat
Údržba a analýza popisných dat patří k běžným funkcím všech informačních systémů. Jedná se o tyto funkce:
- editace popisných dat (provádění změn v popisných datech)
- dotazy na popisná data (včetně vytváření nových popisných dat výběrem)
Pokud jsou popisná data uložena v relační databázi, využívají se pro jejich údržbu a analýzu služby RDBMS a jazyka SQL.
Integrovaná analýza prostorových a popisných dat
Integrovanou analýzou prostorových a popisných dat se liší GIS od ostatních informačních systémů, které mají implementovány pouze funkce operující nad popisnými daty, a od systémů CAD, které mají implementovány pouze (některé) funkce nad prostorovými daty.
Analytické funkce mohou být realizovány dvojím způsobem:
- funkce je realizována pomocí jedné úlohy (jedním procesem)
- pomocí několika navazujících úloh (procesů, modulů)
Výhodou prvního způsobu je snadnost obsluhy, výhodou druhého je širší spektrum možností, které poskytuje modulární systém.
Třídy těchto funkcí:
- Výběry, klasifikace, měření dat - v těchto funkcích jsou zpracovávány obě složky geografických dat (prostorová i popisná - fyzikální), mění se pouze popisná složka dat.
- Operace překryvů (overlay) - řeší aritmetické nebo logické operace mezi vrstvami GIS.
- Operace se sousedními prvky - vyhodnocují charakteristiky území v okolí zadaného prvku.
- Incidenční operace - zpracovávají prvky, které spolu incidují.
- Prostorové statistiky
- Prostorové interakce
Standardizace
Potreba integrácie viacerých systémov, zastrešené organizáciou OGC.
Známe štandardy:
- WMS: http interface (rastrové)
- WFS: http interface (vektorové)
- GML: XML na popis dát
- WPS: poskytovanie výpočtu na webe
Předměty
Použité zdroje
- DRÁŠIL, Milan. PV019 –- Úvod do geoinformačních systémů : Fólie k přednášce (podzim 2011) [online]. 2011. Brno, 2011, 2011-10-17 [cit. 2011-10-29]. Dostupné z WWW: <https://is.muni.cz/el/1433/podzim2011/PV019/um/PV019_2011_part.pdf?info>.
- Richter, Rudolf. PA049 Geografické informační systémy II (přednášky). FI MU, Brno. Dostupné z <https://is.muni.cz/auth/el/1433/jaro2011/PA049/um/>
Vypracoval
Adam Libuša, https://is.muni.cz/auth/osoba/173122, 173122[AT]mail.muni.cz
Malo by byť hotovo. Čerpal som hlavne zo skrípt GISov 1. Ešte sa pozriem na GISy 2, či je tam niečo prínosné a potom napíšem Drášilovi.


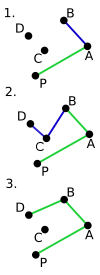

Diskuze
Doplnil som podotázky: Datové modely, Analytické funkce. Chcem sa Vás spýtať viete čo presne spadá pod podotázku „DB prostředky“? Vopred dikes za odpoveď.
Díky za doplnenie. Až po vypracovaní som si všimol, že otázka nie je moc rozdelená podľa podotázok zadania, tak s tým ešte niečo urobím. Čo sa týka databázových prostriedkov, myslím si, že to sú tie indexové štruktúry (R stromy atď).
pekne zpracovana otazka. Diky.
Jedina vec, kterou jsem pobral az po nahlidnuti na wikipedii byla Loxodroma - mozna bych uvedl nakej nazornej obrazek pro lepsi predstavu (napr ten z wiki).
Odkazy som doplnil, diky.