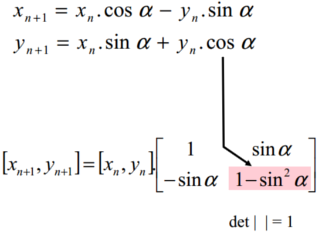Obsah
Zadání
Kreslení grafických primitiv, rastrové algoritmy DDA, s rozhodovacím členem. Rasterizace a vyplňování rovinných primitiv. Ořezávací algoritmy.
Rasterizace
Rasterizace je proces převodu vektorové reprezentace obrazových dat na jejich rastrovou formu s cílem dosáhnout maximální možnou kvalitu a zároveň rychlost výsledného zobrazení.
Při zobrazování je rasterizace velmi často opakovaná operace!
Realizována v HW grafické karty. 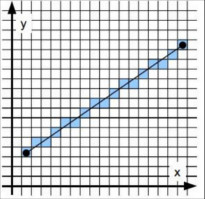
Algoritmy pro vykreslení jsou typicky odvozeny pro případ, kdy obrazec leží v prvním kvadrantu, je rostoucí odpočátečního bodu P1 ke koncovému P2 a nejrychleji roste ve směru osy X. Ostatní místa vykreslování je potřeba převést na tento případ (prohození souřadnic, os, apod.).
DDA - Digital Differential Analyser
Používá floating-point aritmetiku, pro úsečky a kružnice.
Nízká efektivita, náročná implementace do HW.
Vykreslujeme po pixelu od bodu P1 k bodu P2. V ose X postupujeme s přírůstkem dx = 1. V ose Y je přírůstek dán velikostí směrnice objektu. Souřadnice Y se zaokrouhluje na nejbližší celé číslo.
Úsečka
Definice souřadnicemi dvou koncových bodů nebo rovnicí přímky popisující geometrii.
Obecná rovnice úsečky
Parametrické vyjádření
Směrnicový tvar
DDA algoritmus pro úsečku
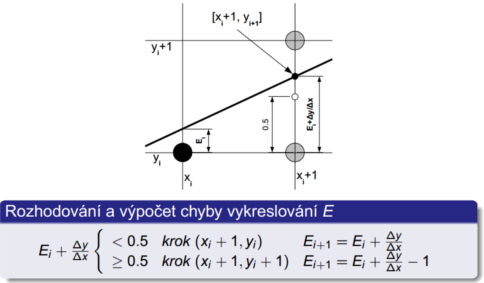
Error control DDA
Modifikace DDA algoritmu. V ose X postupujeme s přírůstkem dx = 1 , v ose Y vyjádříme relativní odchylku E = k. Pokud je E >= 0.5, posouváme se na další řádek a E = E − 1.
Rozhodovací člen – Bresenhamův algoritmus
Pseudokód
Kružnice
Definice souřadnicemi středu a hodnotou poloměru.
Obecná rovnice
Symetrická po půlkvadrantech – obvykle rasterizujeme polovinu prvního kvadrantu, zbylé body zkopírujeme se změnou (prohozením) souřadnic.
Naivní algoritmus
Vykreslujeme po bodech ve směru hodinových ručiček od pixelu [0, R]. Postupujeme po jednom bodu v ose x dokud není x = y, potom postupujeme po jednom bodu v ose y. Floating-point aritmetika, složité v HW. 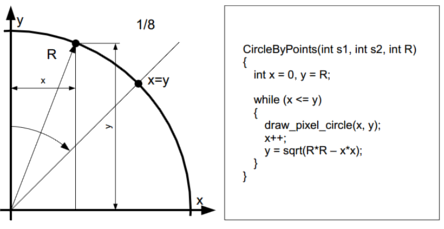
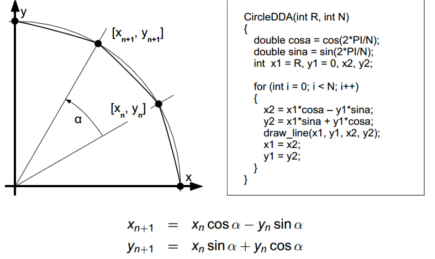
DDA algoritmus pro kružnici
Midpoint
S rozhodovací členem - variace na Bresenhamův algoritmus.
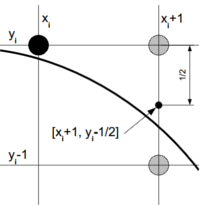
Určování polohy „midpointu“ vůči kružnici – vevnitř nebo vně. Celočíselná aritmetika, snadná implementace v HW. Posouvání po 1 bodě v x-ové souřednici, v y-ové podle znaménka rozhodovacího členu. 

Elipsa
Definice souřadnicemi středu, hodnotami hlavní a vedlejší poloosy a úhlem natočení hlavní poloosy. Obecná rovnice:
Symetrie kvadrantů – vykreslíme jeden kvadrant a ostatní zkopírujeme se změnou souřadnic.
Midpoint algoritmus
Pro oblast I jdeme postupujeme po jednom pixelu v ose x od bodu [0,b], dokud není . Pak pro oblast II až do bodu [a,0] postupujeme po jednom pixelu v ose y. Rozhodovací člen podobně jako pro kružnici.

Vyplňování
Semínkové vyplňování
Naivní rekurzivní algoritmus. „Zasadíme“ semínko do bodu. Algoritmus obarví aktuální bod a otestuje své okolí, zda lze obarvit. Pokud ano, spustí se pro obarvitelné okolní body znova (rekurzivně).
Hraniční varianta vyplňuje až dokud nenarazí na zadanou hraniční barvu. 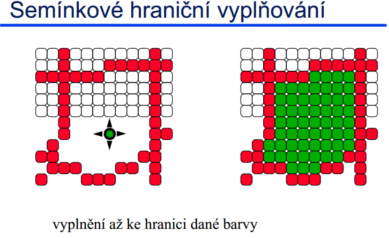
Přebarvení jedné barvy naopak vyplňuje, dokud je v okolí stejná barva jako na počátku (možnost přidat toleranci např. pro malé rozdíly). 
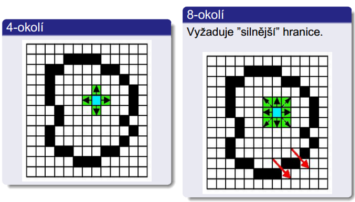
Okolí
- 4-okolí - pro situace, kdy jsou hranice „šišaté“ a rasterizovány jen jedním pixelem
- 8-okolí - pro situace, kdy se rasterizované hranice mohou diagonálně dotýkat, přestože ve vektorové reprezentaci byly malé mezery
Modifikace semínkového vyplňování po řádcích
Od semínka obarvujeme pixely vodorovně na obě strany, při nalezení přiléhající oblasti k vyplnění zasadíme jedno semínko na její začátek.
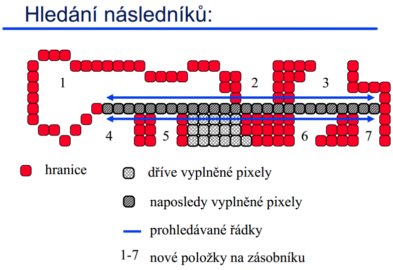
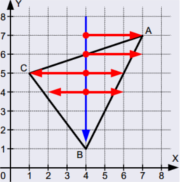
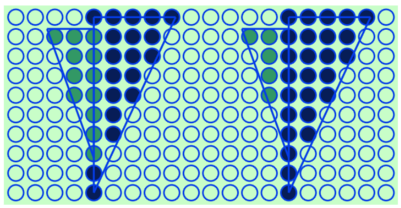
Řádkové vyplňování
Nalezneme bounding-box objektu. Řádky v něm procházíme z jedné strany. Při průchodu hranou přepneme obarvování – po lichých hranách obarvujeme, po sudých vypínáme obarvování.
Problém – vnitřní vrcholy
Řešení:
- V potřebných extrémech generovat dva průsečíky (zde se obarvování vypne a hned zapne)
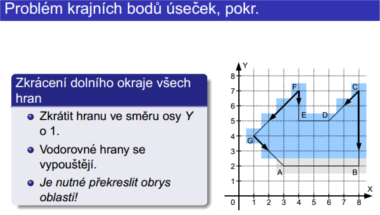
- Zkrácení všech hran ve směru Y o 1 px. Potřeba překreslit obrys
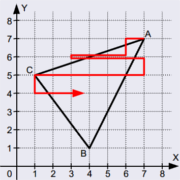
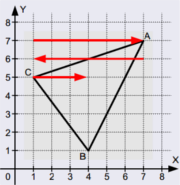
Inverzní řádkové vyplňování
V bounding-boxu objektu od každé hrany napravo po řádcích „zinverzníme“ vyplnění (vyplníme tam, kde není vyplněno, zrušíme vyplnění tam, kde je vyplněno). Vynecháme vodorovné hrany (y1 = y2). Nutno překreslit obrys. 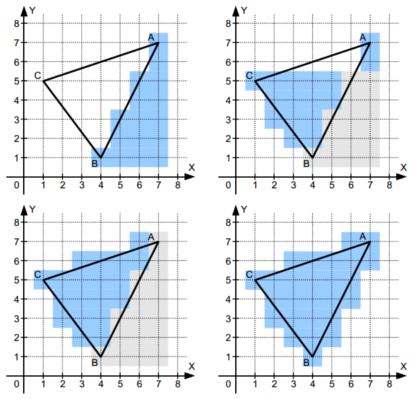
Optimalizace: Plotové vyplňování
Inverze po řádcích jen ke zvolenému plotu (svislice od některého vrcholu). Vždy od strany směrem k plotu. Méně zbytečných operací. 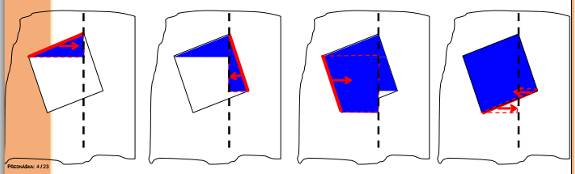
Pinedův algoritmus
Pouze konvexní mnohoúhelníky (typicky trojúhelníky). Rozdělení roviny na oblasti dané polorovinami úseček polygonu. Určíme, které poloroviny jsou vevnitř a které vně. Právě v oblastech, které jsou pouze vnitřní, provedeme vybarvení. Vnitřní a vnější oblast určíme jako vpravo a vlevo (hrany jsou seřazeny podle hodinových ručiček). Snadné v HW. 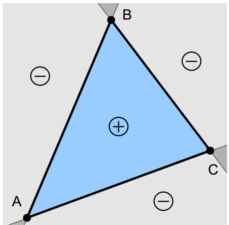
Vyplnění
- Postupujeme v opsaném obdélníku. Zbytečný průchod 1/2 pixelů
- Začneme nejvyšším vrcholem, při nárazu na hranu otáčíme. Algoritmicky složitější
- Od „plotu“ ve středu (opsaného obdélníka). Možná paralelizace
Problémy vykreslování
Možno „odstranit“ (spíše zamaskovat) antialiasingem (částečným překrytím).
Sdílené nebo překrývající se hrany
Střípek
Pohyblivé střípky
Další možnosti vykreslování
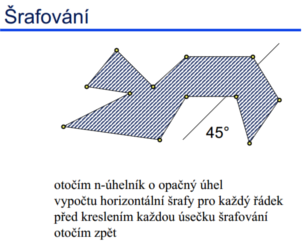
Šrafování
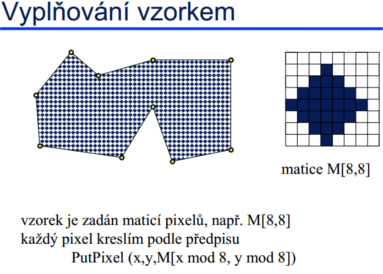
Vyplňování vzorkem
Ořezávání
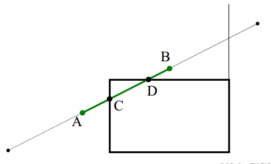
Výběr zobrazovaných objektů vzhledem k aktuální poloze a rozměrům zobrazovacího okna. Objekty mimo okno budou vyloučeny. Objekty, které hranice okna protínají, budou rozděleny (oříznuty). Výsledkem vždy objekt stejného typu (úsečka, polygon, atd.), jako původní.
Naivní ořezávání
pro každou úsečku
pro každou hranu okna
nalezni průsečík přímky s přímkou
vyber „skutečné“ průsečíky
pokud něco zbylo, tak to nakresli
Algoritmus Cohen-Sutherland (ACS)
Optimalizace naivního algoritmu: vyloučíme zbytečný výpočet průsečíků pomocí dělení – mnoho úseček leží vně okna, mnoho úseček uvnitř okna (rovnou je přijmeme nebo zamítneme). 
Pokud oba konce úsečky leží uvnitř okna (test oproti všem čtyřem stranám okna), úsečku triviálně přijmeme. Pokud oba konce úsečky leží ve vnější polorovině některé strany, úsečku triviálně odmítneme.
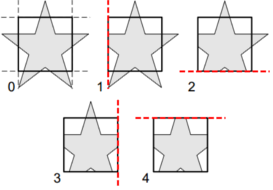
Průniky polorovin označujeme binárně: 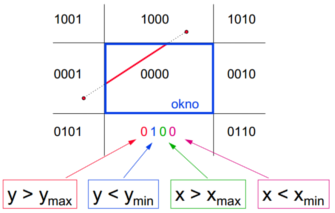
Polohu testujeme binárními operacemi podle polohy koncových bodů a
:
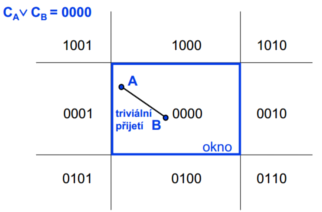
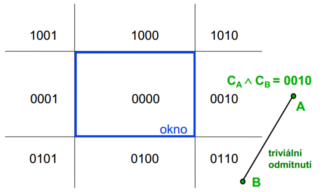
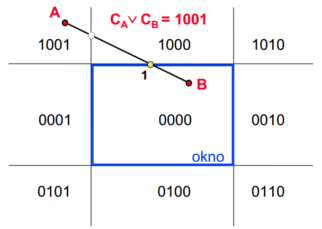
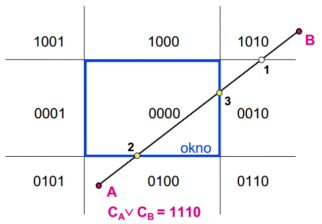
Pseudokód
Vypočti binární kódy koncových bodů C_A, C_B. Je-li (CA and CB) != 0, celá úsečka leží vně okna, odmítni. Je-li (CA or CB) = 0, celá úsečka leží uvnitř okna, přijmi. Pro každou jedničku v (C_A or C_B) postupně ořezávej úsečku.
např. pro Ymax počítej:
X = X_A + (X_B - X_A) * (Y_max - Y_A ) / (Y_B - Y_A) Y = Y_max (A or B) = [X,Y], oprav kód C_A nebo C_B
Nalezení průsečíku s oknem půlením intervalu (neefektivní).
Nejlepší algoritmus, pokud většinu úseček triviálně přijmeme / zamítneme
Parametrické ořezávání
Reprezentace hran okna a testovaných úseček v parametrickém tvaru. Rozhodnutí o viditelných částech pomocí testu bodu úsečky násobenou normálou hranice okna. Podle znaménka leží bod uvnitř(-)/vně(+)/na hraně(0). 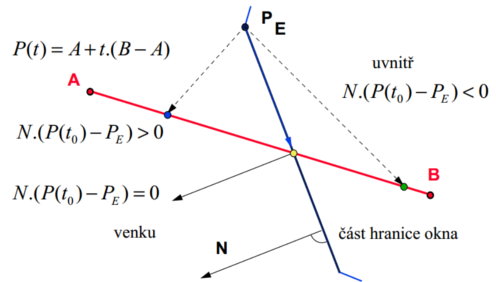
Algoritmus Cyrus-Beck (ACB)
Pro určení, která část leží kde (ne po pixelech úsečky, ale po částech). 
Výpočet t-průsečíků nenáročný. Výpočet (x,y) ořezaných bodů je proveden jen jednou. Neuvažuje triviální přijetí/odmítnutí ⇒ nejlepší algoritmus, pokud se musí hodně ořezávat.
algoritmus Liang-Barsky
Optimalizace Cyrus-Beck pro obdélníkové okno. Zjednodušení výpočtů pro normály: (-1, 0), (1, 0), (0, -1), (0, 1)
Výběr konstantních bodů na hranách.
Řešení pro t:
- (x0 - xleft ) / (x1 - x0 )
(x0 - xright ) / -(x1 - x0 )
- (y0 - ybottom) / (y1 - y0 )
(y0 - ytop ) / -(y1 - y0 )
Problémy ořezávání
Posun
Úsečky jsou reprezentovány celočíselně – při ořezání se změní (zaokrouhlí se na jiný pixel).
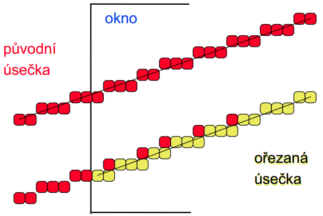
Rozhodovací člen pro interpolátor je třeba vypočíst na základě průsečíku s hranicí, pak teprve rasterizovat.
Ořezávání n-úhelníků
Jestliže chceme kreslit pouze obrys n-úhelníku, pak stačí ořezávat hrany samostatně jako úsečky chceme-li vybarvovat vnitřek n-úhelníku, musíme oříznout speciálním algoritmem. 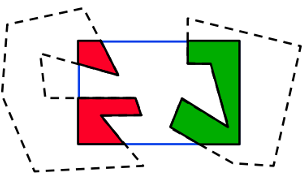
Algoritmus Sutherland-Hodgman
Použité zdroje
doc. Ing. Přemysl Kršek, Ph.D., Ing. Michal Španěl : IZG - Základy počítačové grafiky, slajdy. 2008. Ústav počítačové grafiky a multimédií, Fakulta informačních technologií, Vysoké ucení technické. Brno.
Josef Pelikán, Jiří Sochor : PB009 - Základy počítačové grafiky, slajdy. 2012. Fakulta informatiky, Masarykova Univerzita. Brno.
Počítačová grafika, slajdy. Univerzita Pardubice. http://school.lynn.cz/grafika/prednasky/PG_2006_P04_Vyplnovani_4s.pdf [online].