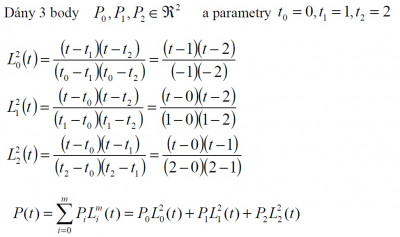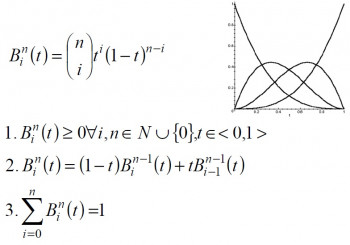Toto je starší verze dokumentu! —-

−Obsah

Zadanie
Vypracovanie
Doplňujúce odkazy na rozšírenie problematiky
Použité zdroje

Zadanie

Křivky a plochy. Parametrické křivky, Interpolační křivky, Hermite, Bezier, Coons, NURBS. Spojitost, změna stupně, podmínky pro hladké navázání. Parametrické plochy. Plochy dané okrajem, tečné vektory. Bezierovy plochy, B-spline plochy, NURBS. Plátování, hladké navázání. Implicitní povrchy, dělené povrchy.

Vypracovanie

Krivky sú obyčajne v počítači reprezentované ako sústava parametrov nejakej rovnice, ktorá je následne generatívne zobrazovaná. Toto vyjadrenie môže byť v podstate trojaké – explicitné, implicitné a parametrické.

Explicitne zadaná krivka je vyjadrená funkciou $y = f(x)$ a býva orientovaná v smere rastúceho $x$ . Takto však môžu byť vyjadrené len krivky, ktoré sú zároveň funkciami, teda jednej hodnote z definičného oboru $x$ zodpovedná jedna funkčná hodnota $y$ .

Implicitne zadaná krivka je vyjadrená rovnicou $F(x,y) = 0$ . Táto reprezentácia je pomerne ťažko zobraziteľná, pretože neumožňuje postupný výpočet krivky. (Tieto krivky sú základom tzv. level set metód v spracovaní obrazu, viď PA166.)

Parametrický tvar krivky ju chápe ako dráhu pohybúceho sa bodu, ktorého súradnice sú funkciami parametru $t$ , teda času, a vyjadruje sa rovnicami $x = x(t)$ , $y = y(t)$ a $z = z(t)$ . Čas je z intervalu $t \in <t_{min}, t_{max}>$ , najčastejšie volený v rozsahu $t \in <0, 1>$ . Výhodou parametrického zápisu krivky je možnosť zachytiť priebeh, kedy krivka prechádza viackrát v rôznych časových okamihoch rovnakými bodmi v priestore (môže sa skrížiť, uzavieť a podobne).
Uvedenými parametrickými funkciami je určená buď bodová rovnica krivky $Q(t) = [x(t), y(t), z(t)]$ , alebo vektorová rovnica $\vec{q}(t) = (x(t), y(t), z(t))$ .
Dotykový vektor (tečný vektor) v bode $Q(t_{0})$ je určený deriváciami parametricky vyjadrenej krivky po zložkách v tvare $\vec{q}(t_{0}) = (x'(t_{0}), y'(t_{0}), z'(t_{0})) = \left(\frac{dx(t_{0})}{dt}, \frac{dy(t_{0})}{dt}, \frac{dz(t_{0})}{dt}\right)$ . Rovnica dotyčnice (tečny) v danom bode má tvar $P(u) = Q(t_{0}) + u.\vec{q'}(t_{0})$ . Vektor $\vec{q'}(t)$ sa nazýva smerový vektor priamky. Parametrická reprezentácia ľahko vyjadruje dotyčnice ku krivke, čo sa využíva pri skladaní kriviek (viac v časti o spojitosti kriviek).

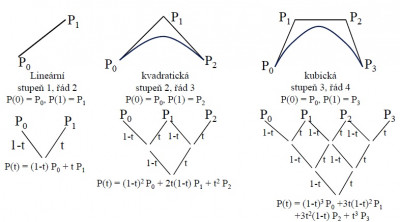
Parametrické krivky

Základným druhom parametrických kriviek používaných v počítačovej grafike sú krivky polynomiálne.

$Q_{n}(t) = a_{0} + a_{1}(t) + ... + a_{n}(t)^{n}$

Výhodou je, že polynomiálne krivky vieme ľahko vyčísliť a sú jednoducho diferencovateľné. Z nich často skladáme krivky po častiach polynomiálne, ktorých segmenty sú polynomiálnymi krivkami. Najčastejšie používame krivky 3. stupňa – kubiky. Pri nich vieme napríklad zaručiť $C^{2}$ spojitosť. Modelovanie týchto kriviek prebieha pomocou definovania tzv. riadiacich bodov. Existujú 2 spôsoby interpretácie riadiacich bodov – interpolácia a aproximácia. Krivka generovaná pri interpolácií prebieha danými bodmi, avšak pri aproximácií je tvar krivky riadiacimi bodmi len určený, prechádzať nimi ale nemusí.

Parametricky zadaná kubika má tvar
$x(t) = a_{x}t^{3} + b_{x}t^{2} + c_{x}t + d_{x}$ $y(t) = a_{x}t^{3} + b_{x}t^{2} + c_{x}t + d_{x}$ $z(t) = a_{x}t^{3} + b_{x}t^{2} + c_{x}t + d_{x}$ ,
čo môžeme v maticovom tvare zapísať ako
$Q(t) = \mathbf{T}.\mathbf{C} = \begin{bmatrix}t^{3} & t^{2} & t & 1\end{bmatrix}.\begin{bmatrix}a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ c_{x} & c_{y} & c_{z} \\ d_{x} & d_{y} & d_{z}\end{bmatrix}$ a jej dotykový vektor $\vec{q'}(t)$ získame deriváciou vektoru $\mathbf{T}$ , teda $\vec{q'}(t) = \frac{d}{dt}\mathbf{T}.\mathbf{C} = \begin{bmatrix}3t^{2} & 2t & 1 & 0\end{bmatrix}.\mathbf{C}$ .
V prípade kubík môžeme maticu rozpísať do súčinu $\mathbf{C} = \mathbf{M}.\mathbf{G}$ , kde $\mathbf{M}$ je bázová matica a $\mathbf{G}$ je vektor geometrických podmienok, ktorý obsahuje konkrétne parametre ovplyvňujúce tvar krviky (riadiace body a dotykové vektory). Súčin $\mathbf{T}.\mathbf{M}$ potom definuje polynomiálnu bázu (skupinu polynómov), ktorá je spoločná pre všetky krivky určitého typu. Tieto polynómy spolu s násobenými geometrickými podmienkami sa uplatňujú ako premenlivé váhy riadené parametrom $t$ . Hodnota parametru potom určuje uplatnenie podmienky buď na začiatku krivky, vo vnútornom priebehu, alebo má najväčší vplyv na koncovú časť.
$Q(t) = \mathbf{T}.\mathbf{M}.\mathbf{G} = \begin{bmatrix}t^{3} & t^{2} & t & 1\end{bmatrix}.\begin{bmatrix}m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34} \\ m_{41} & m_{42} & m_{43} & m_{44}\end{bmatrix}.\begin{bmatrix}G_{1} \\ G_{2} \\ G_{2} \\ G_{4}\end{bmatrix}$

Interpolačné krivky

Základným spôsobom ako interpolovať funkciu zadanú v diskrétnych bodoch je použiť Langrangeov interpolujúci polynóm (po česky interpolačný).

Nevýhodou je nutnosť prepočítať všetky bázické polynómy, ak sa rozhodneme pridať ďalší uzlový bod. Uveďme si príklad výpočtu Lagrangeovho polynómu 2. stupňa.

Po výpočte príkladu získavame krivku zadanú polynómom $P(t) = P_{0}.\left(\frac{t^{2} - 3t + 2}{2}\right) - P_{1}.\left(t^{2} - 2t\right) + P_{2}.\left(\frac{t^{2} - t}{2}\right)$ .

Hermite

Najznámejšie interpolačné krivy používané v počítačovej grafike sú Hermitovské krivky, hlavne Hermitovské kubiky (tiež aj Fergusonove kubiky). Sú určené dvoma riediacimi bodmi $P_{0}$ , $P_{1}$ a dvomi dotykovými vektormi $\vec{p'}_{0}$ , $\vec{p'}_{1}$ . Body určujú začiatočný a koncový bod krivky, smer a veľkosť vektorov jej vyklenutie. Čím je vektor väčší, tým viac sa k nemu krivka primkýna. Ak sú obidva vektory nulové, jedná sa vlastne o úsečku.

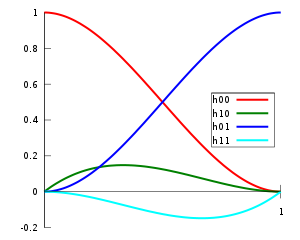
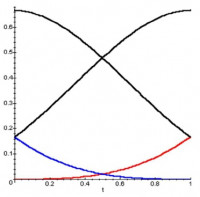
Predpis pre výpočet Hermitovskej kubiky má tvar
$Q(t) = \begin{bmatrix}t^{3} & t^{2} & t & 1\end{bmatrix}.\begin{bmatrix}2 & -2 & 1 & 1 \\ -3 & 3 & -2 & -1 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0\end{bmatrix}.\begin{bmatrix}P_{0} \\ P_{1} \\ \vec{p'}_{0} \\ \vec{p'}_{1}\end{bmatrix} = P_{0}.F_{1}(t) + P_{1}.F_{2}(t) + \vec{p'}_{0}.F_{3}(t) + \vec{p'}_{1}.F_{4}(t)$ ,
kde dostávame tzv. kubické Hermitovské polynómy (Hermitovské polynómy 3. stupňa)
$F_{1}(t) = 2t^{3} - 3t^{2} + 1$ (červený),
$F_{2}(t) = -2t^{3} + 3t^{2}$ (modrý),
$F_{3}(t) = t^{3} - 2t^{2} + t$ (zelený),
$F_{4}(t) = t^{3} - t^{2}$ (cyan).
Výhoda týchto kubík sa prejavuje pri ich nadväzovaní, keďže dotykové vektory v koncových bodoch sú priamo súčasťou definície. Napr. spojitosť $C^{1}$ je zaručená totožnosťou koncových bodov a identitou dotykových vektorov v týchto bodoch či spojitosť $G^{1}$ docielime lineárnou závislosťou dotykových vektorov (viď spojitosť kriviek). Hermitovské kubiky sú aj základom animačných kriviek Kochanek-Bartels (viď otázka 13-gra).

Aproximačné krivky

Béziér

Bézierove krivky sa používajú častejšie na modelovanie v dvoch rozmeroch, napríklad pri definícii fontov. Bézierove krivky $n$ -tého stupňa sú určené $n + 1$ bodmi riadiaceho polynómu $P_{i}$ . Medzi vlastnosti patrí, že zmenou polohy jedného riadiaceho bodu dôjde k zmene tvaru celej krivky. Preto sa krivky často delia na segmenty nižšieho stupňa (napr. kubiky), ktoré sa postupne naväzujú.

$Q(t) = \sum_{i=0}^{n} P_{i}B_{i}^{n}(t)$

Základom Bézierových kriviek sú Bernsteinove polynómy $n$ -tého stupňa.

Medzi vlastnosti Bernsteinovych polynómov patrí ich nezápornosť (1), súčet váh vždy 1 (3), teda výsledná krivky bude ležať v konvexnej obálke bodov riadiaceho polynómu. Rekurentná definícia (2) vychádza z lineárnej kombinácie polynómov nižšieho stupňa.

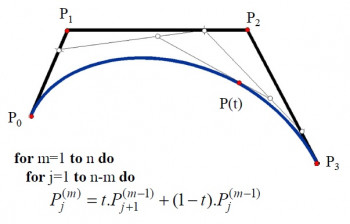
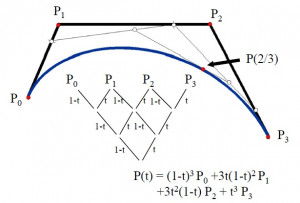
Na konštrukciu Bézierovej krivky sa používa rekurzívny algoritmus deCasteljau. Vstupom algoritmu sú riadiace body polygónu. Výstupom je bod krivky v určitom čase $t$ . Na druhom obrázku vidíme príklad výpočtu a schému výpočtu bodu Bézierovej kubiky v čase $t = 2/3$ .

Bézierova kubika je určená 4 bodmi $P_{0}$ , $P_{1}$ , $P_{2}$ a $P_{3}$ (zápis kubiky $P(t)$ vidíme na druhom obrázku). Popisujú ju 4 Bernsteinove polynómy 3. stupňa (vidíme ich graficky znázornené na obrázku s vlastnosťami Bernsteinových polynómov). Zaujímavé sú dotykové vektory $\vec{p'}(0) = 3(P_{1} - P_{0})$ a $\vec{p'}(1) = 3(P_{3} - P_{2})$ . Z tohto vzťahu pre dotykové vektory je totiž zrejmý jednoduchý a priamočiary prevod medzi Bézierovou kubikou a kubikou v Hermitovskej reprezentácii.

B-spline, Coons

Prirodzený spline je po častiach polynomiálna krivka, ktorá interpoluje svoje riadiace body. Prirodzený kubický spline sa skladá z polynomiálnych kriviek 3. stupňa a vo svojich uzloch je $C^{2}$ spojitý.

V počítačovej grafike sa najčastejšie používa ale B-spline, ktorý nie je prirodzený (interpolačný), ale jedná sa o krivku aproximačnú. Poznáme dva základné typy – uniformný neracionálny a neuniformný racionálny.

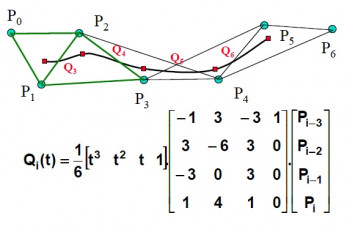
Uniformný neracionálný B-splajn nazývame tiež Coonsova kubika. Je určená 4 riadiacimi bodmi $P_{0}$ , $P_{1}$ , $P_{2}$ a $P_{3}$ . Priebeh bázových polynómov Coonsových kubík môžeme vidieť na obrázku. Segment takejto krivky teda na rozdiel od Bézierových kriviek neprechádza krajnými bodmi svojho riadiaceho polygónu. Dosedením $t = 0$ do maticového zápisu (vidíme ho na obrázku) zistíme, že krivka začína v bode ležiacom v jednej tretine ťažnice pri $P_{1}$ trojuholníka určeného prvými 3 bodmi (teda $P_{0}$ , $P_{1}$ a $P_{2}$ ). Takisto aj koncový bod krivky (na obrázku je krivka zaznačená ako segment $Q_{3}$ ) v čase $t = 1$ leží v tretine ťažnice pri $P_{2}$ trojuholníka určeného bodmi $P_{1}$ , $P_{2}$ a $P_{3}$ .

Coonsov B-spline vzniká naväzovaním Coonsových kubík, je teda určená 4 a viacerými bodmi ( $n \geq 4$ ). Skladá sa potom z $n - 3$ segmentov. Každý segment $Q_{i}$ je určený bodmi $P_{i-3}$ , $P_{i-2}$ , $P_{i-1}$ a $P_{i}$ . Koncový bod jedného segmentu a ziačiatočný bod ďalšieho segmentu majú rovnaké prvé a druhé derivácie, teda Coonsove krivky sú v uzloch $C^{2}$ spojité.

Medzi dôležité vlastnosti B-spline kriviek patrí invariancia (nemennosť) voči otočeniu, posunutiu a zmene mierky. B-spline leží celý v konvexnej obálke určenej jeho riadiacimi bodmi. Zmenou polohy niektorého z riadiacich bodov sa zmení len tá časť krivky, ktorá je týmto bodom určená. Ak posunieme bod $P_{i}$ , zmení sa tvar štyroch segmentov $Q_{i}$ , $Q_{i+1}$ , $Q_{i+2}$ a $Q_{i+3}$ .

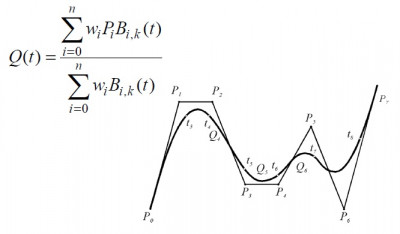
NURBS

Neuniformné racionálne B-spline krivky sú zovšeobecnením vyššie uvedených B-spline kriviek. Neuniformné sú ale preto, lebo vzdialenosť uzlov v zmysle parametru $t$ nemusí byť konštantná. Racionálne znamená, že body sú reprezentované svojimi homogénnymi súradnicami. Krivka NURBS je určená minimálne 4 bodmi $P_{0},..., P_{n}$ riadiaceho polygónu, rádom $k$ (kde najvyšší stupeň polynómu je $k - 1$ ) a uzlovým vektorom $(t_{0},..., t_{n+k})$ , ktorý je tvorený postupnosťou neklesajúcich reálnych čísel – uzlových hodnôt.

V zápise NURBS krivky je $w_{i}$ váha $i$ -tého bodu riadiaceho polygónu a $B_{i,k}(t)$ sú normalizované B-spline bázové funkcie. Pre váhu $w = 0$ krivku stredný riadiaci bod neovplyvňuje (je z nej úsečka), váhe $w = 1$ zodpovedá prípad neracionálnej krivky. So zvyšujúcou váhou sa krivka k riadiacemu bodu stále viac primkýna. Pri $w = \infty$ krivka bodom prechádza a dochádza tak k strate spojitosti. Podmienka nezápornosti váh zaručuje umiestnenie krivky v konvexnej obálke.

Podobne ako u Bézierových kriviek a Bernsteinových polynómov majú aj NURBS polynómy analogické vlastnosti ako nezápornosť či to, že výsledná krivka bude ležať v konvexnej obálke bodov riadiaceho polynómu. Rekurentná definícia vychádza z lineárnej kombinácie dvoch polynómov nižších stupňov. Tento rekurentný vzťah je základom Cox-deBoorovho algoritmu na výpočet bodov NURBS krivky, ktorý je zovšeobecnením algoritmu deCasteljau pre spline krivky s neuniformnou parametrizáciou.

Základom kriviek NURBS je to, že umožňujú presne definovať kuželosečky a to za pomoci spomínaných váhových koeficientov. Medzi vlastnosti kriviek ďalej patrí invariancia voči transformáciam a voči rovnobežnému stredovému premietaniu.

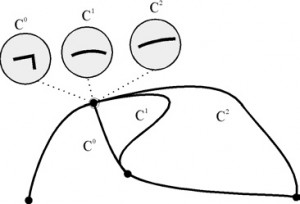
Spojitosť

Predpokladajme, že $Q_{1}(t)$ a $Q_{2}(t)$ su dve časti (segmenty) jedinej krivky $Q(t)$ spojenej v bode $Q_{1}(t) = Q_{2}(t)$ nazývanom uzol (knot). Spojitosť (continuity) je možné zjednodušene označiť ako spôsob napojenia týchto dvoch segmentov v uzle.

Hovoríme, že $Q(t)$ je triedy $C^{n}$ , ak má vo všetkých bodoch spojité derivácie podľa parametru $t$ do rádu $n$ . Označenie $C^{n}$ sa nazýva parametrická spojitosť stupňa n.

$C^{0}$ – dva segmenty sú spojito naviazané, ak je koncový bod prvého segmentu počiatočným bodom segmentu druhého
$C^{1}$ – ak dotykový (tečný) vektor v koncovom bode prvého segmentu je rovný dotykovému vektoru druhého segmentu v jeho počiatočnom bode
$C^{2}$ – analogicky je požadovaná rovnosť vektoru prvej a druhej derivácie

Čím vyššia je spojitosť, tím dlhšiu „dobu“ (v zmysle parametru $t$ ) oba segmenty akoby sledujú rovnaký smer. Zjavne platí vzťah $C^{n+1} \Rightarrow C^{n}$ , teda napr. ak je krivka spojitá $C^{2}$ , tak je spojitá aj $C^{1}$ . Bod sa pohybuje po spojitej dráhe a v bode $C^{0}$ môže skokom meniť smer pohybu, rýchlosť i zrýchlenie. V bode $C^{1}$ nemôže skokom zmeniť smer pohybu a veľkosť rýchlosti, v bode $C^{2}$ sa nemôže zmeniť ani zrýchlenie.

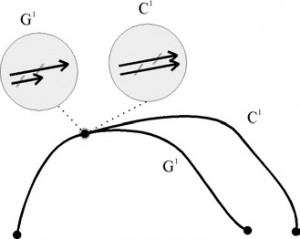
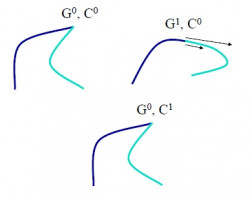
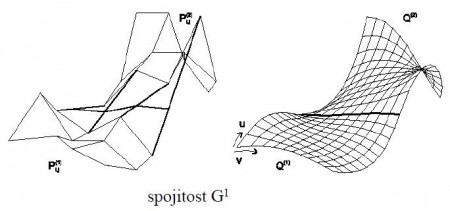
Hladkosť naviazania môžeme posudzovať tiež podľa tzv. geometrickej spojitosti stupňa n označovanej $G^{n}$ . Najčastejšie sa používajú spojitosti $G^{0}$ a $G^{1}$ .

$G^{0}$ – ak je koncový bod prvého segmentu totožný s počiatočným bodom druhého segmentu (osobne si myslím, že môžeme tvrdiť, niečo v zmysle $G^{0} = C^{0}$ )
$G^{1}$ – ak sú $G^{0}$ spojité a súčasne sú dotykové vektory segmentov súhlasne kolineárne, teda platí $\vec{q'_{1}}(1) = k.\vec{q'_{2}}(0); k > 0$

Táto spojitosť nezaručuje totožnosť dotykových vektorov (tečných vektorů), ale len dotyčníc (tečen). Jednoducho vektory majú zhodný smer, nie však veľkosť. V bode $G^{1}$ sa nemení skokom smer pohybu, môže sa ale zmeniť jeho rýchlosť (krivka je vizuálne hladká). Spojitosť $G^{1}$ je „skoro rovnaká“ ako $C^{1}$ , ale zaručiť spojitosť $G^{1}$ je oveľa jednoduchšie ako $C^{1}$ . Môžme povedať, že $C^{1} \Rightarrow G^{1}$ , ale výnimku tvorí prípad, kedy vektor rýchlosti v mieste spojenia dvoch segmentov je $(0,0,0)$ . Opačná implikácia neplatí, pretože geometrická spojitosť nepostihuje rýchlosť a zrýchlenie pohybu.

(Rozpisovaním presných rovníc jednotlivých derivácií vás tu nechcem zaťažovať. Nie je v nich nič, čo by sa nedalo takto elegantne slove popísať. V prípade záujmu viď slajdy PB009 uvedené v použitých zdrojoch.)

(Tento obrázok ze zo slajdov predmetu PB009. Myslím si ale, že tretí príklad je chybne. Možno sa tým chcelo ukázať, že vektory majú rovnakú veľkosť, rozhodne ale nemajú rovnaký smer, takže parametrická spojitosť prvého stupňa tam byť nemôže. Keď tak ma, prosím, opravte. )

Parametrické plochy

Vyjadrenie plochy môže byť podobne ako u krivky len s doplnením ďalšej dimenzie – explicitné, implicitné a parametrické.

Explicitne zadaná plocha je vyjadrená funkciou $z = f(x,y)$ .

Implicitne zadaná plocha je vyjadrená rovnicou $F(x,y,z) = 0$ (podrobnejšie v časti o implicitných plochách).

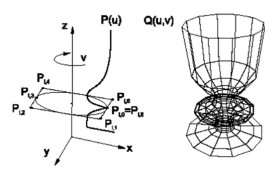
Parametrickým vyjaderním plochy $Q(u,v)$ je bodová rovnica dvoch parametrov $u$ a $v$ nadobúdajúcich hodnoty z intervalu $<0,1>$ , ktorá je zadaná ako $Q(u,v) = [x(u,v), y(u,v), z(u,v)]$ .

Dotykový vektor (tečný vektor) $\vec{q_{u}}(u,v)$ v smere parametru $u$ k ploche $Q(u,v)$ a dotykový vektor $\vec{q_{v}}(u,v)$ v smere parametru $v$ sú určené vzťahmi
$\vec{q_{u}}(u,v) = \frac{\partial Q(u,v)}{\partial u}) = \left(\frac{\partial x(u,v)}{\partial u}, \frac{\partial y(u,v)}{\partial u}, \frac{\partial z(u,v)}{\partial u}\right)$ ,
$\vec{q_{v}}(u,v) = \frac{\partial Q(u,v)}{\partial v}) = \left(\frac{\partial x(u,v)}{\partial v}, \frac{\partial y(u,v)}{\partial v}, \frac{\partial z(u,v)}{\partial v}\right)$ .

Rovnica dotykovej roviny (tečné roviny) je určené ako $T(r,s) = Q(u,v) + r.\vec{q_{u}} + s.\vec{q_{v}}; r,s \in R$ .
Skruty (skrutové vektory) charakterizujú „vyklenutie“ plochy v miestach napojenia. Sú definované pomocou zmiešaných parciálnych derivácií ako $\vec{q_{uv}}(u,v) = \frac{\partial^{2}Q(u,v)}{\partial u \partial v}$ .
Normálu (kolmicu) k ploche v bode $Q$ určíme ako normalizovaný vektorový súčin dotykových vektorov, teda $\vec{n} = \frac{\vec{q_{u}} \times \vec{q_{v}}}{|\vec{q_{u}} \times \vec{q_{v}}|}$ .

Hlavná krivka plochy v smere parametru $u$ je každá krivka určená rovnicou $Q(u,k)$ pevného parametru $k$ a premenného parametru $u$ . Analogicky to platí aj pre hlavnú krivku v smere parametru $v$ . Rohy plochy sú body $Q(0,0)$ , $Q(1,0)$ , $Q(0,1)$ a $Q(1,1)$ . Strany plochy $Q(u,v)$ sú hlavné krivky v oboch smeroch, kde pevný parameter má hodnotu $0$ alebo $1$ . Všetky strany dohromady tvoria okraj plochy.

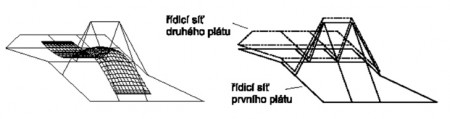
Analógiou naväzovania segmentov a ich skladania do krivky aj plochy sa skladajú z častí, ktoré voláme pláty. Naväzovanie plôch sa nazýva plátovanie. AJ pri plochách rozoznávame parametrickú spojitosť $C$ a gemometrickú spojitosť $G$ . Napríklad dva pláty sú $C^{1}$ spojité, ak majú spoločnú stranu a priečne parciálne derivácie vo všetkých bodoch spoločnej strany sú zhodné.

Plochy sa zadávajú riadiacimi bodmi a bázovými funkciami. Väčšinou sa používajú plochy aproximačné. Interpolácia vo viac ako dvoch dimenziách je náročná a vyžaduje rozsiahle výpočty. Interpolačná plocha $P_{ij}$ má $(m + 1) \times (n + 1)$ bodov. Interpoláciou vektorovým polynómom je možné plochu zapísať ako $\vec{P}(u,v) = \sum_{i=0}^{m} \sum_{j=0}^{n} b_{ij}.u^{i}.v^{j}$ .

Na aproximačné vyjadrenie plôch sa používajú tzv. 12-vektorový Hermitovský plát alebo 16-vektorový (obsahuje navyše 4 skrutové vektory v každom rohu plátu).

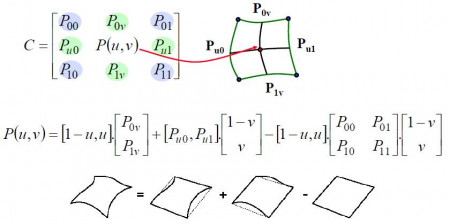
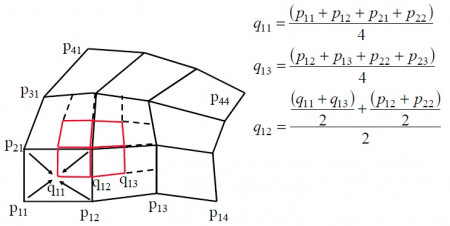
Plochy zadané okrajom

Plochy môžu byť zadané aj pomocou všetkých kriviek určujúcich okraj, napr. 4 v prípade štvoruholníkového plátu.

Bilineárna Coonsova plocha je jednoznačne určená štyrmi krivkami $P(u,0)$ , $P(u,1)$ , $P(0,v)$ a $P(1,v)$ , ktoré musia tvoriť uzavretý okraj budúceho plátu.
Rovnica, ktorá určuje bilineárnu Coonsovu plochu sa dá zjednodušene zapísať v tvare $[1-u,-1,u].\mathbf{C}.[1-v,-1,v]^{T} = 0$ , kde bod uprostred matice $\mathbf{C}$ je hľadaným riešením tejto implicitnej rovnice. Na výpočet bilineárnej plochy však slúži explicitné vyjadrenie tejto rovnice, ktoré môžeme vidieť na obrázku spolu s grafickým znázornením výpočtu. Zásadným problémom plochy je, že zo zadaného okraja nie je možné jednoducho vyjadriť priečne dotykové vektory a teda nie je ľahké vytvoriť hladké spojenie dvoch takýchto plátov.

Bikubická plocha je rovnako určená štyrmi krivkami, ale popísaná vzťahom $[F_{1}(u),-1,F_{2}(u)].\mathbf{C}.[F_{1}(v),-1,F_{2}(v)]^{T} = 0$ , kde dané funkcie predstavujú Hermitovské polynómy $F_{1}(t) = 2t^{3} - 3t^{2} + 1$ a $F_{2}(t) = -2t^{3} + 3t^{2}$ . Pre rovnaké dôvody ako v predchádzajúcom prípade, ani tieto plochy sa nepoužívajú na plátovanie so spojitou prvou deriváciou.

Až všeobecná bikubická plocha (po česky obecná) umožňuje hladké naväzovanie plátov, keďže je pri nej potrebné zadávať aj dotykové vektory podľa okraja. Okrem 4 spomínaných kriviek ju preto určujú aj priečne vektory pozdĺž okrajov $\vec{p_{v}}(u,0)$ , $\vec{p_{v}}(u,1)$ , $\vec{p_{u}}(0,v)$ a $\vec{p_{u}}(1,v)$ . Ďalej je tiež určená skrutmi v jednotlivých rohoch, teda vektormi $\vec{t}(0,0)$ , $\vec{t}(0,1)$ , $\vec{t}(1,0)$ a $\vec{t}(1,1)$ .
Vzťah pre všeobecnú bikubickú plochu je rozšírený o ďalšie dva Hermitovské polýnómy tretieho stupňa $F_{3}(t) = t^{3} - 2t^{2} + t$ , $F_{4}(t) = t^{3} - t^{2}$ a implicitná rovnica plochy má tvar $[F_{3}(u),F_{1}(u),-1,F_{2}(u),F_{4}(u)].\mathbf{C}.[F_{3}(v),F_{1}(v),-1,F_{2}(v),F_{4}(v)]^{T} = 0$ .

Bézierove plochy

Bézierove plochy používajú niektoré modelovacie systémy k reprezentácii povrchu telies, pretože sú ľahko diferencovateľné, jednoducho sa modelujú a tiež je pomerne ľahko môžné vypočítať priesečník s lúčom. Tieto plochy sú vlastne špeciálnym prípadom zložitejšej reprezentácie povrchov pomocou NURBS.

Na obrázku vidíme definíciu Bézierovej plochy, kde bázové funkcie $B_{i}^{m}$ a $B_{j}^{n}$ predstavujú Bernsteinove polynómy $m$ -tého (resp. $n$ -tého) stupňa.

Bézierova plocha pri zmene jedného riadiaceho bodu zmení celý svoj tvar. Táto vlastnosť je nevýhodná, a preto sa plochy plátujú. Pre napojenie plátov so spojitosťou nultého stupňa musíme zabezpečiť stotožnenie riadiacich bodov, ktoré určujú príslušnú stranu. Na obrázku vidíme príklad napojenia s geometrickou spojitosťou prvého stupňa ( $G^{1}$ ), ktorá vzniká vtedy, ak sú priečne dotykové vektory lineárne závislé.

Metódou na zobrazovanie Bézierových plôch je polygonizácia založená na princípe rekurzívneho delenia (patch splitting), pričom sa využíva algoritmus deCasteljau.

B-spline plochy

Pre modelovanie sú B-spline plochy oveľa výhodnejšie, pretože sa naväzujú omnoho jednoduchšie než Hermitovské alebo Bézierove pláty. B-spline plochy $n$ -tého stupňa totiž zaručujú $C^{n-1}$ spojitosť vo všetkých svojich bodoch. ďalšou výhodou je, že zmenou jedného riadiaceho bodu zmeníme vždy iba časť danej plochy.

Medzi vlastnosti B-spline plochy patrí:

celá plocha leží v konvexnej obálke svojich riadiacich bodov,
pri zmene riadiaceho bodu sa zmenia iba pláty, ktoré sú ním určené
plocha síce všeobecne neprechádza krajnými bodmi plochy, je to ale možné dosiahnuť násobnými riadiacimi bodmi
sú invariantné k lineárnym transformáciam (otočenie, posun, zmena mierky, skosenie)

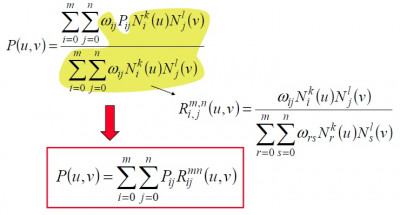
NURBS plochy

Neuniformné racionálne B-spline plochy sú zovšeobecnením B-spline plôch a predstavujú dnes štandard v priemyslovom modelovaní. Umožňujú definovať širokú škálu plôch, napr. voľne tvarovateľné plochy na báze racionálnych polynómov (free form surfaces) alebo plochy založené na priamkách a kuželosečkách. Aj ich vznik datujeme do polovice 20. storočia pre potreby presnej matematickej reprezentácie tvaru karosérie áut, trupu lodí či lietadiel.

Z definície, $N_{i}^{k}(u)$ a $N_{j}^{l}(v)$ sú normalizované B-spline bázové funkcie ( $k$ , $l$ sú stupne polynómu) a $\omega_{i,j}$ sú váhy jednotlivých bodov (homogénne súradnice) riadiace siete $\mathbf{P}$ . Váhy podobe ako v prípade kriviek určujú vplyv riadiaceho bodu na plochu, pričom so zvyšujúcou sa hodnotou váhy sa plocha k bodu primkýna. Podobne ako Bézierove plochy, aj NURBS sú invariantné k lineárnym transformáciam a vďaka racionalite sú naviac invariantné aj k perspektívnej projekcii.

O plochách NURBS hovoríme aj v prípade modelovacej techniky zvanej šablónovanie (sweeping), kde patria napríklad:

translačné šablónovanie - obrys je ľubovoľný a trajektória, po ktorej je obrys ťahaný je úsečka, dostávame tzv. priamkové plochy popísané vzťahom $Q(u,v) = (1-u).P(0,v) + u.P(1,v)$ , typy translačného šablónovania sú – po úsečke s nemeniacou sa profilovou krivkou (extruded surface), po úsečke medzi danými profilmi (ruled surface) a poťahovanie (skinning),
rotačné šablónovanie - obrys je ľubovoľný a trajektória, po ktorej je obrys ťahaný je kružnica alebo jej časť – toto teleso je možné získať aj rotáciou okolo osi, výsledkom je rotačná plocha (viď obrázok),
všeobecné šablónovanie - obrys i trajektória je ľubovoľná, získavame zovšeobecnenú valcovú plochu.

Implicitné povrchy

Implicitné vyjadrenie plochy tvorí alternatívu k povrchu definovanom pomocou polygónov alebo parametrických plátov. Výhodou je napríklad kompaktnejšia reprezentácia či jednoduchšie sledovanie lúča (paprsku). Výpočet sledovania lúča je ale časovo náročný, rovnako je náročné aj zobrazovanie plochy v reálnom čase. Väčšina zobrazovacích metód v konečom dôsledku aj tak prevádza implicitné plochy na parametrické vyjadrenie alebo rovinné plošky, tzv. polygonizácia implicitných plôch.

Funkcia $f(x,y,z)$ priraďuje každému bodu v priestore nejakú skalárnu hodnotu a definuje teda skalárne pole. Nami hľadaný objekt je izoplocha, teda množina bodov s rovnakou funkčnou hodnotou. Ak $f = 0$ , bod leží na povrchu plochy. Ak $f < 0$ alebo $f > 0$ , možeme hovoriť, že bod leží vo vnútri (alebo vonku) objektu ohraničeného plochou, no ktorá hodnota označuje čo, už závisí na konkrétnom kontexte.

Normály povrchu sú obvykle určené gradientom príslušnej funkcie, teda $\nabla f(x,y,z) = \left(\frac{df}{dx}, \frac{df}{dy}, \frac{df}{dz}\right)$ .

Medzi implicitné povrchy zaraďujeme blobby objekty (kvapky) od J. Blinna, metaballs či soft objects od Wyvilla.

Príkladom implicitnej plochy (množiny bodov $P$ v trojrozmernom priestore) je guľová plocha zadaná implicitnou rovnicou $Q(P) = x^{2} + y^{2} + z^{2} = r^{2}$ .

Implicitné plochy môžu byť reprezentované aj takzvanými dištančnými povrchmi (viď zoznam na obrázku).

Delené povrchy

Modely sú reprezentované pomocou mnohouholníkov, avšak len málokedy majú objekty reálneho sveta ostré hrany. Pri modelovaní pomocou polygónov nastávajú problémy s úrovňou detailov. Aj keď model aproximujeme dostatočným množstvom polygónov, pri zväčšení sa problém hrán znovu objaví. Riešením je delenie povrchov.

Polygonálna sieť je množina vrcholov a prepojení medzi nimi, čím definuje topológiu povrchu a vymedzuje jednotlivé plošky. Delenie je rekurzívny proces, pri ktorom je polygónová sieť zjemňovaná pridávaním vrcholov a plošiek. Pri zvyšovaní počtu vrcholov síce dochádza k výraznému spomaleniu a takéto modely sú pamäťovo náročné, ale aj napriek tomu je zjemňovanie siete významné pri tvorbe animácií a statických modelov. Generované povrchy, kedy zvyšujeme úroveň detailov sa nazývajú delené povrchy (subdivision surfaces).

Povrchy môžeme deliť nad poškami alebo deliť nad vrcholmi. Dôležitým faktorom pri delení povrchov je topológia polygónovej siete. Môže sa jednať napríklad o trojuholníkovú sieť, štvorcovú sieť alebo sieť s ľubovoľnou topológiou. Obidve nasledujúce prezentované deliace schémy však dokážu deliť povrchy s ľubovoľnou topológiou, čo je ich veľká výhoda.

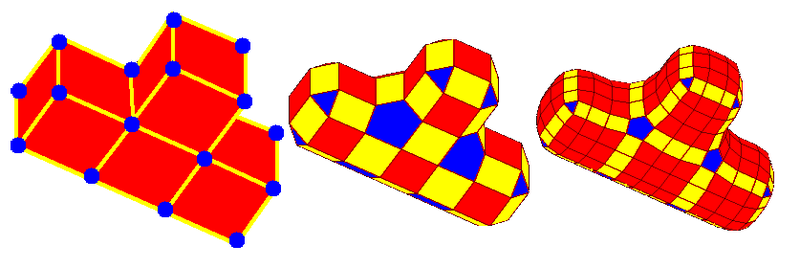
Doo-Sabin

Doo-Sabin je aproximačná deliaca schéma používajúca delenie nad vrcholmi.

Ploškový bod je vypočítaný ako priemer všetkých vrcholov plošky podľa vzťahu $V_{F} = \frac{1}{N} \sum_{i=1}^{N} V_{i}$ . Pre každý vrchol potom vypočítame nový vrchol prislúchajúci k pôvodnému ako priemer ploškového bodu, pôvodného vrcholu a stredu hrán, ktoré z neho vychádzajú, teda $V' = \frac{V + V_{F} + M_{E1} + M_{E2}}{4}$ . Takto vznikajú 3 typy nových plošiek – plošková (červená), hranová (žltá) a vrcholová (modrá).

Povrchy generované delením Doo-Sabin spĺňajú podmienku $C^{1}$ spojitosti (okrem hranice, kde je sieť otvorená).

Catmull-Clark

(Tu môžete spomenúť, docent Sochor to má rád , oskarový krátkometrážny animovaný film od štúdia Pixar „Geriho hra (1997)“, ktorý režíroval český rodák Jan Pinkava a pri jeho tvorbe bola naplno využitá práve deliaca schéma Catmull-Clark (viac informácií v článku http://graphics.pixar.com/library/Geri/paper.pdf).)

Catmull-Clark je aproximačná deliaca schéma používajúca delenie nad ploškami.

Podobne ako pri delení Doo-Sabin, aj tu si spočítame poškový bod $V_{F}$ , avšak zatiaľ čo v predchádzajúcom prípade plnil len funkciu medzivýsledku pri výpočte nových bodov, teraz sa stáva súčasťou výslednej zjemnenej siete. Ďalej určíme hranový bod $V_{E}$ ako priemer vrcholov hrany a ploškových bodov podľa vzťahu $V_{E} = \frac{E_{1} + E_{2} + V_{F1} + V_{F2}}{4}$ . Posledný typ bodu, ktorý musíme spočítať je vrcholový bod $V_{V}$ zjednodušene vyjadrený vzťahom $V_{V} = \frac{Q + 2R + S.(n-3)}{n}$ , kde $Q$ je priemer nových stenových bodov na stenách priľahlých k vrcholu, $R$ je priemer nových hranových bodov a $S$ je pôvodný vrchol.

Povrchy generované delením Catmull-Clark spĺňajú podmienku $C^{1}$ spojitosti (mimo výnimočné vrcholy dokonca až spojitosť $C^{2}$ ).

Doplňujúce odkazy na rozšírenie problematiky

http://bspline.webuda.com/ - diplomová práca z UK o B-splajnoch, obsahuje nejaké applety na vizualizáciu a vyčerpávajúci text.

http://www.netgraphics.sk/b-splajnove-krivky - stránka v slovenčine aj angličtine taktiež s množstvom Java appletov. Prekračuje však len problematiku kriviek a venuje sa rôznym témam počítačovej grafiky.

http://www.hyperkrychle.cz/curves/ - ďalšia diplomová práca o krivkách, tentokrát z VUT.

http://www.ibiblio.org/e-notes/Splines/Intro.htm, http://www.vis.uni-stuttgart.de/~kraus/LiveGraphics3D/cagd/ - anglické texty a opäť veľké množstvo appletov na vizualizáciu kriviek.

Použité zdroje

ŽÁRA, Jiří., BENEŠ, Bedřich., SOCHOR, Jiří., FELKEL, Petr. Moderní počítačová grafika. Brno, CZ: Computer Press, 2004. 612 s. ISBN 80-251-0454-0.

SOCHOR, Jiří. Študijné materiály k predmetu „PB009 Základy počítačové grafiky“. Křivky v počítačové grafice [online]. Brno, CZ: Masarykova univerzita, 2013.

mgr-szz/in-gra/5-gra.1414397272.txt.gz · Poslední úprava: 2020/04/12 16:56 (upraveno mimo DokuWiki)

Nahoru