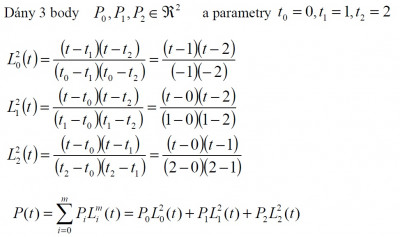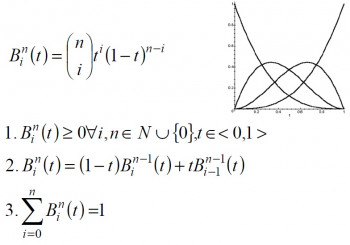Toto je starší verze dokumentu!
—-
Obsah
Zadanie
Parametrické křivky, Lagrange, Hermite, Bezier, Coons, NURBS. Spojitost, změna stupně, podmínky pro hladké navázání. (PB009, PA010)
Vypracovanie
Krivky sú obyčajne v počítači reprezentované ako sústava parametrov nejakej rovnice, ktorá je následne generatívne zobrazovaná. Toto vyjadrenie môže byť v podstate trojaké – explicitné, implicitné a parametrické.
Explicitne zadaná krivka je vyjadrená funkciou a býva orientovaná v smere rastúceho
. Takto však môžu byť vyjadrené len krivky, ktoré sú zároveň funkciami, teda jednej hodnote z definičného oboru
zodpovedná jedna funkčná hodnota
.
Implicitne zadaná krivka je vyjadrená rovnicou . Táto reprezentácia je pomerne ťažko zobraziteľná, pretože neumožňuje postupný výpočet krivky. (Tieto krivky sú základom tzv. level set metód v spracovaní obrazu, viď PA166.)
Parametrický tvar krivky ju chápe ako dráhu pohybúceho sa bodu, ktorého súradnice sú funkciami parametru , teda času, a vyjadruje sa rovnicami
,
a
. Čas je z intervalu
, najčastejšie volený v rozsahu
. Výhodou parametrického zápisu krivky je možnosť zachytiť priebeh, kedy krivka prechádza viackrát v rôznych časových okamihoch rovnakými bodmi v priestore (môže sa skrížiť, uzavieť a podobne).
Uvedenými parametrickými funkciami je určená buď bodová rovnica krivky , alebo vektorová rovnica
.
Dotykový vektor (tečný vektor) v bode je určený deriváciami parametricky vyjadrenej krivky po zložkách v tvare
. Rovnica dotyčnice (tečny) v danom bode má tvar
. Vektor
sa nazýva smerový vektor priamky. Parametrická reprezentácia ľahko vyjadruje dotyčnice ku krivke, čo sa využíva pri skladaní kriviek (viac v časti o spojitosti kriviek).
Parametrické krivky
Základným druhom parametrických kriviek používaných v počítačovej grafike sú krivky polynomiálne.
Výhodou je, že polynomiálne krivky vieme ľahko vyčísliť a sú jednoducho diferencovateľné. Z nich často skladáme krivky po častiach polynomiálne, ktorých segmenty sú polynomiálnymi krivkami. Najčastejšie používame krivky 3. stupňa – kubiky. Pri nich vieme napríklad zaručiť spojitosť. Modelovanie týchto kriviek prebieha pomocou definovania tzv. riadiacich bodov. Existujú 2 spôsoby interpretácie riadiacich bodov – interpolácia a aproximácia. Krivka generovaná pri interpolácií prebieha danými bodmi, avšak pri aproximácií je tvar krivky riadiacimi bodmi len určený, prechádzať nimi ale nemusí.
Parametricky zadaná kubika má tvar
,
čo môžeme v maticovom tvare zapísať ako
a jej dotykový vektor
získame deriváciou vektoru
, teda
.
V prípade kubík môžeme maticu rozpísať do súčinu , kde
je bázová matica a
je vektor geometrických podmienok, ktorý obsahuje konkrétne parametre ovplyvňujúce tvar krviky (riadiace body a dotykové vektory). Súčin
potom definuje polynomiálnu bázu (skupinu polynómov), ktorá je spoločná pre všetky krivky určitého typu. Tieto polynómy spolu s násobenými geometrickými podmienkami sa uplatňujú ako premenlivé váhy riadené parametrom
. Hodnota parametru potom určuje uplatnenie podmienky buď na začiatku krivky, vo vnútornom priebehu, alebo má najväčší vplyv na koncovú časť.
Interpolačné krivky
Zá
kladným spôsobom ako interpolovať funkciu zadanú v diskrétnych bodoch je použiť Langrangeov interpolujúci polynóm (po česky interpolační).
Nevýhodou je nutnosť prepočítať všetky bázické polynómy, ak sa rozhodneme pridať ďalší uzlový bod. Uveďme si príklad výpočtu Lagrangeovho polynómu 2. stupňa.
Po výpočte príkladu získavame krivku zadanú polynómom .
Hermite
Najznámejšie interpola
čné krivy používané v počítačovej grafike sú Hermitovské krivky, hlavne Hermitovské kubiky (tiež aj Fergusonove kubiky). Sú určené dvoma riediacimi bodmi ,
a dvomi dotykovými vektormi
,
. Body určujú začiatočný a koncový bod krivky, smer a veľkosť vektorov jej vyklenutie. Čím je vektor väčší, tým viac sa k nemu krivka primkýna. Ak sú obidva vektory nulové, jedná sa vlastne o úsečku.
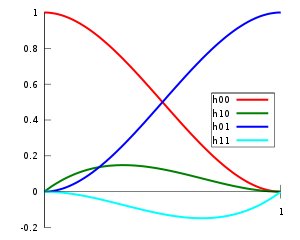
Predpis pre výpočet Hermitovskej kubiky má tvar ,
kde dostávame tzv. kubické Hermitovské polynómy (Hermitovské polynómy 3. stupňa) (červený),
(modrý),
(zelený),
(cyan).
Výhoda týchto kubík sa prejavuje pri ich nadväzovaní, keďže dotykové vektory v koncových bodoch sú priamo súčasťou definície. Napr. spojitosť je zaručená totožnosťou koncových bodov a identitou dotykových vektorov v týchto bodoch či spojitosť
docielime lineárnou závislosťou dotykových vektorov (viď spojitosť kriviek). Hermitovské kubiky sú aj základom animačných kriviek Kochanek-Bartels (viď otázka 13-gra).
Aproximačné krivky
Béziér
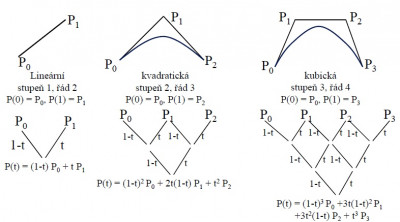
Bézierove krivky sa používajú častejšie na modelovanie v dvoch rozmeroch, napríklad pri definícii fontov. Bézierove krivky -tého stupňa sú určené
bodmi riadiaceho polynómu
. Medzi vlastnosti patrí, že zmenou polohy jedného riadiaceho bodu dôjde k zmene tvaru celej krivky. Preto sa krivky často delia na segmenty nižšieho stupňa (napr. kubiky), ktoré sa postupne naväzujú.
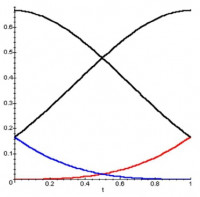
Základom Bézierových kriviek sú Bernsteinove polynómy -tého stupňa.
Medzi vlastnosti Bernsteinovych polynómov patrí ich nezápornosť (1), súčet váh vždy 1 (3), teda výsledná krivky bude ležať v konvexnej obálke bodov riadiaceho polynómu. Rekurentná definícia (2) vychádza z lineárnej kombinácie polynómov nižšieho stupňa.
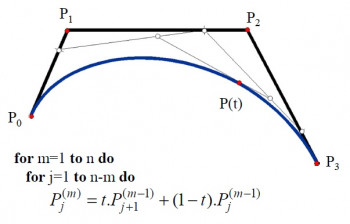
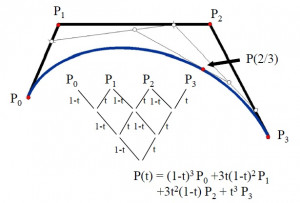
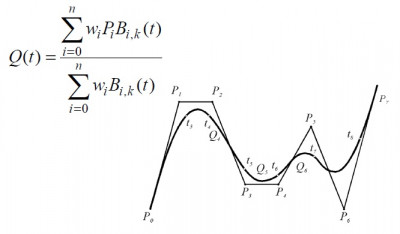
Na konštrukciu Bézierovej krivky sa používa rekurzívny algoritmus deCasteljau. Vstupom algoritmu sú riadiace body polygónu. Výstupom je bod krivky v určitom čase . Na druhom obrázku vidíme príklad výpočtu a schému výpočtu bodu Bézierovej kubiky v čase
.
Bézierova kubika je určená 4 bodmi ,
,
a
(zápis kubiky
vidíme na druhom obrázku). Popisujú ju 4 Bernsteinove polynómy 3. stupňa (vidíme ich graficky znázornené na obrázku s vlastnosťami Bernsteinových polynómov). Zaujímavé sú dotykové vektory
a
. Z tohto vzťahu pre dotykové vektory je totiž zrejmý jednoduchý a priamočiary prevod medzi Bézierovou kubikou a kubikou v Hermitovskej reprezentácii.
B-spline, Coons
Prirodzený spline je po častiach polynomiálna krivka, ktorá interpoluje svoje riadiace body. Prirodzený kubický spline sa skladá z polynomiálnych kriviek 3. stupňa a vo svojich uzloch je spojitý.
V počítačovej grafike sa najčastejšie používa ale B-spline, ktorý nie je prirodzený (interpolačný), ale jedná sa o krivku aproximačnú. Poznáme dva základné typy – uniformný neracionálny a neuniformný racionálny.
Uniformný neracionálný B-splajn nazývame tiež Coonsova kubika. Je určená 4 riadiacimi bodmi ,
,
a
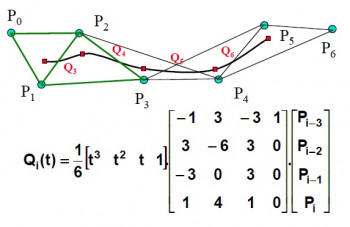
. Priebeh bázových polynómov Coonsových kubík môžeme vidieť na obrázku. Segment takejto krivky teda na rozdiel od Bézierových kriviek neprechádza krajnými bodmi svojho riadiaceho polygónu. Dosedením
do maticového zápisu (vidíme ho na obrázku) zistíme, že krivka začína v bode ležiacom v jednej tretine ťažnice pri
trojuholníka určeného prvými 3 bodmi (teda
,
a
). Takisto aj koncový bod krivky (na obrázku je krivka zaznačená ako segment
) v čase
leží v tretine ťažnice pri
trojuholníka určeného bodmi
,
a
.
Coonsov B-spline vzniká naväzovaním Coonsových kubík, je teda určená 4 a viacerými bodmi (). Skladá sa potom z
segmentov. Každý segment
je určený bodmi
,
,
a
. Koncový bod jedného segmentu a ziačiatočný bod ďalšieho segmentu majú rovnaké prvé a druhé derivácie, teda Coonsove krivky sú v uzloch
spojité.
Medzi dôležité vlastnosti B-spline kriviek patrí invariancia (nemennosť) voči otočeniu, posunutiu a zmene mierky. B-spline leží celý v konvexnej obálke určenej jeho riadiacimi bodmi. Zmenou polohy niektorého z riadiacich bodov sa zmení len tá časť krivky, ktorá je týmto bodom určená. Ak posunieme bod , zmení sa tvar štyroch segmentov
,
,
a
.
NURBS
Neuniformné racionálne B-spline krivky sú zovšeobecnením vyššie uvedených B-spline kriviek. Neuniformné sú ale preto, lebo vzdialenosť uzlov v zmysle parametru nemusí byť konštantná. Racionálne znamená, že body sú reprezentované svojimi homogénnymi súradnicami. Krivka NURBS je určená minimálne 4 bodmi
riadiaceho polygónu, rádom
(kde najvyšší stupeň polynómu je
) a uzlovým vektorom
, ktorý je tvorený postupnosťou neklesajúcich reálnych čísel – uzlových hodnôt.
V zápise NURBS krivky je váha
-tého bodu riadiaceho polygónu a
sú normalizované B-spline bázové funkcie. Pre váhu
krivku stredný riadiaci bod neovplyvňuje (je z nej úsečka), váhe
zodpovedá prípad neracionálnej krivky. So zvyšujúcou váhou sa krivka k riadiacemu bodu stále viac primkýna. Pri
krivka bodom prechádza a dochádza tak k strate spojitosti. Podmienka nezápornosti váh zaručuje umiestnenie krivky v konvexnej obálke.
Podobne ako u Bézierových kriviek a Bernsteinových polynómov majú aj NURBS polynómy analogické vlastnosti ako nezápornosť či to, že výsledná krivka bude ležať v konvexnej obálke bodov riadiaceho polynómu. Rekurentná definícia vychádza z lineárnej kombinácie dvoch polynómov nižších stupňov. Tento rekurentný vzťah je základom Cox-deBoorovho algoritmu na výpočet bodov NURBS krivky, ktorý je zovšeobecnením algoritmu deCasteljau pre spline krivky s neuniformnou parametrizáciou.
Základom kriviek NURBS je to, že umožňujú presne definovať kuželosečky a to za pomoci spomínaných váhových koeficientov. Medzi vlastnosti kriviek ďalej patrí invariancia voči transformáciam a voči rovnobežnému stredovému premietaniu.
Spojitosť
Predpokladajme, že a
su dve časti (segmenty) jedinej krivky
spojenej v bode
nazývanom uzol (knot). Spojitosť (continuity) je možné zjednodušene označiť ako spôsob napojenia týchto dvoch segmentov v uzle.
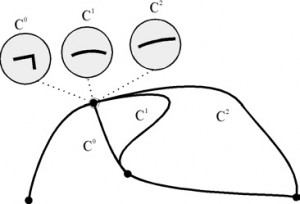
Hovoríme, že je triedy
, ak má vo všetkých bodoch spojité derivácie podľa parametru
do rádu
. Označenie
sa nazýva parametrická spojitosť stupňa n.
– dva segmenty sú spojito naviazané, ak je koncový bod prvého segmentu počiatočným bodom segmentu druhého
– ak dotykový (tečný) vektor v koncovom bode prvého segmentu je rovný dotykovému vektoru druhého segmentu v jeho počiatočnom bode
– analogicky je požadovaná rovnosť vektoru prvej a druhej derivácie
Čím vyššia je spojitosť, tím dlhšiu „dobu“ (v zmysle parametru ) oba segmenty akoby sledujú rovnaký smer. Zjavne platí vzťah
, teda napr. ak je krivka spojitá
, tak je spojitá aj
. Bod sa pohybuje po spojitej dráhe a v bode
môže skokom meniť smer pohybu, rýchlosť i zrýchlenie. V bode
nemôže skokom zmeniť smer pohybu a veľkosť rýchlosti, v bode
sa nemôže zmeniť ani zrýchlenie.
Hladkosť naviazania môžeme posudzovať tiež podľa tzv. geometrickej spojitosti stupňa n označovanej . Najčastejšie sa používajú spojitosti
a
.
– ak je koncový bod prvého segmentu totožný s počiatočným bodom druhého segmentu (osobne si myslím, že môžeme tvrdiť, niečo v zmysle
)
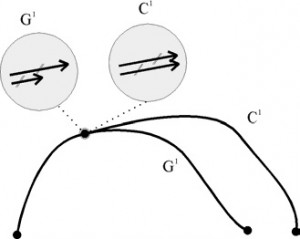
– ak sú
spojité a súčasne sú dotykové vektory segmentov súhlasne kolineárne, teda platí
Táto spojitosť nezaručuje totožnosť dotykových vektorov (tečných vektorů), ale len dotyčníc (tečen). Jednoducho vektory majú zhodný smer, nie však veľkosť. V bode sa nemení skokom smer pohybu, môže sa ale zmeniť jeho rýchlosť (krivka je vizuálne hladká). Spojitosť
je „skoro rovnaká“ ako
, ale zaručiť spojitosť
je oveľa jednoduchšie ako
. Môžme povedať, že
, ale výnimku tvorí prípad, kedy vektor rýchlosti v mieste spojenia dvoch segmentov je
. Opačná implikácia neplatí, pretože geometrická spojitosť nepostihuje rýchlosť a zrýchlenie pohybu.
(Rozpisovaním presných rovníc jednotlivých derivácií vás tu nechcem zaťažovať. Nie je v nich nič, čo by sa nedalo takto elegantne slove popísať. V prípade záujmu viď slajdy PB009 uvedené v použitých zdrojoch.)
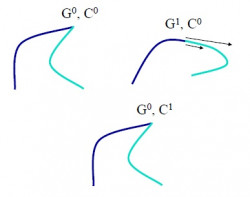
(Tento obrázok ze zo slajdov predmetu PB009. Myslím si ale, že tretí príklad je chybne. Možno sa tým chcelo ukázať, že vektory majú rovnakú veľkosť, rozhodne ale nemajú rovnaký smer, takže parametrická spojitosť prvého stupňa tam byť nemôže. Keď tak ma, prosím, opravte. ![]() )
)
Použité zdroje
ŽÁRA, Jiří., BENEŠ, Bedřich., SOCHOR, Jiří., FELKEL, Petr. Moderní počítačová grafika. Brno, CZ: Computer Press, 2004. 612 s. ISBN 80-251-0454-0.
SOCHOR, Jiří. Študijné materiály k predmetu „PB009 Základy počítačové grafiky“. Křivky v počítačové grafice [online]. Brno, CZ: Masarykova univerzita, 2013.