Toto je starší verze dokumentu! —-

Obsah

IN-POS 2. Algoritmy a datové struktury

IN-POS 2. Algoritmy a datové struktury

Zadání

Analýza složitosti, amortizovaná složitost.
Techniky návrhu algoritmů (rozděl a panuj, dynamické programování, hladové strategie).
Pokročilé datové struktury (haldy, union-find struktury).
Algoritmy pro práci s řetězci (algoritmy Karp-Rabin, KMP, Boyer-Moore, užití konečných automatů).

IV003

Vypracování

Analýza složitosti, amortizovaná složitost

Časová složitost

Časová složitost je funkce velikosti vstupu.

Vyjadřuje závislost času potřebného pro provedení výpočtu na rozsahu (velikosti) vstupních dat.

Rozlišujeme časovou složitost v nejlepším, nejhorším a průměrném případě.

Asymptotická notace

abstrakce od detailů při udávání složitosti

Θ notace

Pro danou funkci $g(n)$ označuje symbol $\Theta(g(n))$ množinu funkcí:

$\Theta(g(n)) = \lbrace f(n) \mid \exists c_1, c_2, n_0 : \forall n \geq n_0: 0\leq c_1g(n) \leq f(n) \leq c_2g(n)$

—

$f(n) \in \Theta(g(n))$ : f roste asymptoticky stejně rychle jako g

O notace

Pro danou funkci $g(n)$ označuje symbol $\mathcal{O}(g(n))$ množinu funkcí:

$\mathcal{O}(g(n)) = \lbrace f(n) \mid \exists c, n_0 : \forall n \geq n_0: 0 \leq f(n) \leq cg(n)$

—

$f(n) \in \mathcal{O}(g(n))$ : f roste asymptoticky rychleji než g

Ω notace

Pro danou funkci $g(n)$ označuje symbol $\Omega(g(n))$ množinu funkcí:

$\Omega(g(n)) = \lbrace f(n) \mid \exists c, n_0 : \forall n \geq n_0: 0 \leq cg(n) \leq f(n)$

—

$f(n) \in \Omega(g(n))$ : f roste asymptoticky pomaleji než g

Složitost problému

Dolní odhad složitosti problému: důkazové techniky
Horní odhad složitosti problému: složitost konkrétního algoritmu pro daný problém
Složitost problému: určeno dolním a horním odhadem, problém těsných odhadů

Techniky

Informační metoda

Řešení obsahuje určité množství informace.
V každém kroku jsme schopni určit pouze část této informace.

Permutace

Generování všech permutací n-prvkové posloupnosti

počet různých permutací: $n!$
⇒ dolní odhad: $\Omega(n!)$
⇒ složitost problému: $\Theta(n!)$

Polynom

Evaluace $a_{n}x^{n} + a_{n-1}x^{n-1} + ... + a_0$ v bodě $x$ .

Spracování všech koeficientů $\Omega(n)$
⇒ dolní odhad: $\Omega(n)$
⇒ složitost problému: $\Theta(n)$

Metoda redukce

známe dolní odhad pro Q
Q redukujeme na P (Q řešíme za pomoci P)
dolní odhad pro Q je i dolním odhadem pro P

Metoda sporu

Snažíme se dokázat dolní odhad složitosti.
Dvě varianty:
- Předpokládáme, že má algoritmus asymptoticky menší složitost a konstruujeme vstup, pro který nevypočte korektní řešení.
- Předpokládáme, že algoritmus najde vždy korektní řešení a konstruujeme vstup, pro který složitost přesáhne uvažovanou mez.

Amortizovaná složitost

Technika pro přesnější určení složitosti.

Analyzujeme posloupnost operací jako celek, ne složitost každé operace.

Používané metody

Seskupení: Operace seskupíme do skupin a analyzujeme složitost celé skupiny operací současně.

Zásobník

Skupina 1: operace PUSH: součet složitostí nepřesáhne n
Skupina 2: operace POP a MULTIPOP
- Součet složitostí (= počet prvků vybraných ze zásobníku) nepřesáhne počet operací PUSH (= počet vložených prvků)
- Složitost celé skupiny je n

Celá posloupnost n operací má v nejhorším případě složitost 2n.

Metoda účtů:
- Každé operaci přiřadíme kredit (číslo), které může být různé od skutečné složitosti.
- Při realizaci zaplatíme skutečnou cenu kredity
  - nedoplatek placen z účtu
  - přebytek vrácen na účet
- Počáteční stav kreditů je 0.
- Pokud je stav kreditů po celou dobu výpočtu nezáporný. Součet kreditů je $\geq$ složitosti vykonaných operací.
- Pro přehlednost lze kredity lze přiřazovat/odebírat objektům, na kterých se operace realizují.

Zásobník

operace	složitost	kredity
PUSH	1	2
POP	1	0
MULTIPOP	$\min(k, \mid S \mid)$	0

Nezápornost kreditů dokážeme pomocí invariantu: „Počet kreditů na účtu je rovný počtu prvků na zásobníku.“
Invariant platí na začátku.
PUSH zaplatí jeden kredit, 1 kredit dáme na účet
POP a MULTIPOP zaplatí kredity z účtu

Celá posloupnost n operací je $\leq$ součet kreditů vykonaných operací.
Součet kreditů vykonaných operací je $\leq 2n$

Potenciálová funkce
- Zvolíme potenciálovou funkci, která přiřadí každého hodnotě datové struktury číslo.
- Po celou dobu výpočtu nesmí hodnota klesnout pod počáteční mez.
- Definujeme amortizované ceny operací pomocí skutečné ceny a změně potenciálu.
- Součet amortizovaných cen je $\geq$ součtu skutečných cen. (Tedy je i horním odhadem složitosti posloupnosti operací.)

Zásobník

operace	složitost	amortizovaná cena
PUSH	1	$1 + (\|S\|+1) - \|S\| = 2$
POP	1	$1 + \|S\| - (\|S\|+1) = 0$
MULTIPOP	$\min(k, \mid S \mid)$	$\begin{cases} k + (\mid S \mid - k) - \mid S \mid = 0 \text{ pro } \mid S \mid \textgreater k \\ \mid S \mid + 0 - \mid S \mid = 0 \text{ pro } \mid S \mid \leq k \end{cases}$

Celá posloupnost n operací je $\leq$ součet amortizovaných cen.
Součet amortizovaných cen je $\leq 2n$

Techniky návrhu algoritmů

Rozděl a panuj

Problém rozděl na podproblémy (stejného typu).
Vyřeš podproblémy.
Z řešení podproblému sestav řešení problému.

Příklady:
- Merge sort
- Quick sort
- Násobení celých čísel
- Násobení matic
- Fast Fourier Transformation

Dynamické programování

Charakteristická struktura problému:
- Problém lze rozdělit na podproblémy.
- Vhodné pro optimalizační problémy s překryvem podproblémů.
- Počet různých podproblémů je polynomiální.
- Optimální řešení problému v sobě obsahuje optimální řešení podproblému.
- Existuje přirozené uspořádání podproblémů od nejmenšího po největší.

Rekurzivní definice hodnoty optimálního řešení.
Výpočet hodnoty optimálního řešení zdola-nahoru.
Z vypočítaných hodnost sestav optimální řešení.

Memoizace = Pamatování si hodnot podproblémů.
➕ jednoduché na pochopení
➖ nutné určit pořadí řešení podproblémů ručně

Bottom-up
➕ nemá overhead způsobený rekurzí
➖jednodušší analýza složitosti

Příklady:
- Floydův alg.
- Warshallův alg.

Hladové strategie

Vhodné pro optimalizační problémy, kde optimální řešení obsahuje optimální řešení podproblémů.
Stačí získat optimální řešení jediného podproblému. (Výběr na základě lokální optimality.)
Postup shora-dolů

Příklady:
- Dijkstrův algoritmus pro problém nejkratších cest z daného vrcholu
- Kruskal a Prim pro nejlehčí kostry
- Huffmanovy kódy
- Problém mincí (placení co nejmenším počtem mincí)
- Problém pásky
  - n souborů různých délek ukládáme postupně na pásku
  - minimalizace přístupového času

Pokročilé datové struktury

Haldy

Halda = Datová struktura pro reprezentaci prvků, nad kterými je definované úplné uspořádání.
Podporované operace:
- MAKE_HEAP() vytvoří prázdnou haldu
- INSERT(H, x) do haldy H
- MINIMUM(H) najde minimální prvek v H
- EXTRACT_MIN(H) z haldy H odstraní minimální prvek
- DELETE(H, x) z hlady H odstraní prvek x
- UNION(H1, H2) vytvoří novou haldu sjednocením H1 a H2
- DECREASE_KEY(H, x, y) nahradí klíč x klíčem y (y < x)

Operace	Seznam	Binární halda	Binomiální halda	Fibonacciho halda
MAKE_HEAP	$\Theta(1)$	$\Theta(1)$	$\Theta(1)$	$\Theta(1)$
MINIMUM	$\Theta(n)$	$\Theta(1)$	$\Theta(\log n)$	$\Theta(1)$
INSERT	$\Theta(1)$	$\Theta(\log n)$	$\Theta(1)$ *	$\Theta(1)$
UNION	$\Theta(1)$	$\Theta(n)$	$\Theta(\log n)$	$\Theta(1)$
EXTRACT_MIN	$\Theta(n)$	$\Theta(\log n)$	$\Theta(\log n)$	$\Theta(\log n)$ *
DELETE	$\Theta(1)$	$\Theta(\log n)$	$\Theta(\log n)$	$\Theta(\log n)$ *
DECREASE_KEY	$\Theta(1)$	$\Theta(\log n)$	$\Theta(\log n)$	$\Theta(1)$ *

* amortizovaná složitost

Binomiální halda

Na rozdíl od binární haldy tvořena lesem binomiálních stromů.
Umožňuje snadné spojování stromů.

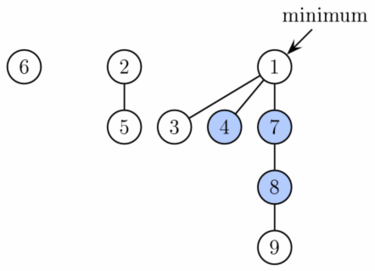
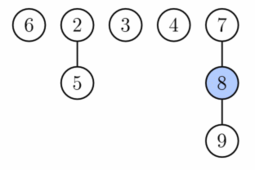
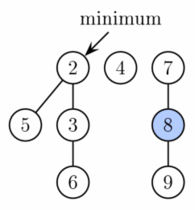
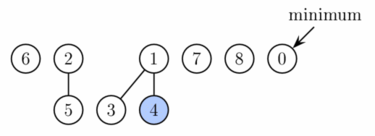
Fibonacciho halda

zobecnění binární haldy
struktura může obsahovat víc stromů; ukládáme ukazatel na minimální prvek
odkládáme operace až na dobu, kdy je to nutné
dvě hlavní mota (viz video Amortized analysis of Fibonacci heap):
- Někdy se vyplatí nechat nepořádek narůst. (A uklidit hromadně.)
  - = Nové uzly přidáváme jako jednouzlové stromy. Stromy se stejným stupněm spojujeme hromadně až při extract-min.
- Tvoji rodiče chtějí hodně vnoučat a pokud nemáš moc dětí, tak tě zavrhnou.
  - = Uzel, který již dvakrát ztratil při decrease-key potomka je přesunut jako nový strom.
Efektivně realizujeme UNION, INSERT a DECREASE_KEY, ale nezhoršujeme amortizovanou složitost ostatních operací.

EXTRACT_MIN

Odebrání prvku (1) a rozpad potomků.

Spojení a finální stav po EXTRACT_MIN

DECREASE_KEY

Snížení hodnoty z (9) na (0)

Union-find struktury

Reprezentace disjunktních množin.
Operace:
- MAKE_SET(x) vytvoří množinu obsahující prvek x
- UNION(H1, H2) vytvoří novou množinu sjednocením H1 a H2
- FIND_SET(x) najde reprezentanta množiny obsahující x

Aplikace:
- Kruskalův agoritmus
- komponenty souvislosti
- ekvivalence konečných automatů

algoritmus	MAKE_SET	UNION	FIND_SET
reverzní stromy	$\mathcal{O}(1)$	$\mathcal{O}(1)$	$\mathcal{O}(n)$
reverzní stromy (optimalizace)	$\mathcal{O}(1)$	$\mathcal{O}(\log n)$	$\mathcal{O}(\log n)$
plytké stromy	$\mathcal{O}(1)$	$\mathcal{O}(\log n)$	$\mathcal{O}(1)$

Stromy s kompresí: Posloupnost m operací UNION, FIND_SET a MAKE_SET, z toho n operací MAKE_SET má složitost $O(m . \alpha(n))$

Reverzní stromy (Reversed trees)

Každá množina reprezentována stromem.
Jeden vrchol stromu odpovídá jednomu prvku množiny.
Každý vrchol obsahuje odkaz na rodiče.
Kořen ukazuje na sebe a je reprezentantem množiny.

Implementace pomocí pole/seznamu.
MAKE_SET, UNION: konstantní složitost
FIND_SET: až lineární k počtu prvků prohledávané množiny

Optimalizace:
- Při spojení dvou množin se kořen menší množiny stane synem kořene větší množiny.
- Ke každému vrcholu asociujeme hloubku stromu jehož je kořenem.
- MAKE_SET konstantní složitost
- UNION, FIND_SET $\mathcal{O}(\log n)$

Plytké stromy (Shallow threaded trees)

Množinu reprezentujeme jako spojovaný seznam, první prvek je reprezentantem.
Každý prvek má ukazatele na následníka a na reprezentanta.
Reprezentant obsahuje údaj o kardinalitě množiny.

MAKE_SET, FIND_SET konstantní složitost
WEIGHTED_UNION $\mathcal{O}(\log n)$ amortizovaná složitost

Stromy s kompresí (Trees with path compresion)

FIND_SET: Při postupu zpět napojíme vrcholy na cestě přímo na kořen.
Posloupnost m operací UNION, FIND_SET a MAKE_SET, z toho n operací MAKE_SET má složitost $O(m . \alpha(n))$

Algoritmy pro práci s řetězci

Některé algoritmy (naivní, Karp-Rabin, automaty) jsou podrobněji rozepsány zde: http://statnice.dqd.cz/home:inf:in17

Algoritmy pro:

Vyhledávání vzorku v textu.
Vzdálenosti řetězců a transformace řetězců
Společná podposloupnost
Aproximace řetězců
Opakující se podřetězce

Algoritmus	Předspracování	Vyhledávání
Úplné prohledávání	$O$	$O((n-m+1)m)$
Karp-Rabin *	$\Theta(m)$	$O((n-m+1)m)$
Konečné automaty	$O(m \|\Sigma\|)$	$\Theta(n)$
Knuth-Morriss-Pratt	$\Theta(m)$	$\Theta(n)$
Boyer-Moore *	$\Theta(m + \|\Sigma\|)$	$O((n-m+1)m)$

* Očekávaná složitost je výrazně lepší.

Karp-Rabin

Řetězce chápeme jako čísla v desítkové soustavě.
Vzorek i jednotlivé podřetězce hašujeme (pomocí Hornerova schématu) a porovnáváme tyto haše.
Při posunutí o jednu pozici jsme schopni přepočíst haš v konstantním čas.

Příprava: $\Theta(m)$
1. Vypočteme haš hledaného řetězce.
2. Vypočteme haš prvního podřetězce.
Výpočet: $O((n-m+1)m)$
1. Porovnáme haš vzorku a haš aktuálního podřetězce. (Pokud je roven, porovnáme řetězce a případně uložíme nalezenou pozici.)
2. Posuneme se o jednu pozici v prohledávaném textu a přepočteme haš (v konstantním čase).
3. Porovnáváme a posouváme se dokud jsme nedosáhli $(m-1)$ -té pozice od konce. Poté vrátíme všechny nalezené pozice.

Očekávaná složitost pro c nálezů: $\mathcal{O}((n-m+1) + cm)$
- ➕ vhodné pro delší vzorky s malým počtem očekávaných nálezů

Užití konečných automatů

Pro daný vzorek zkonstruujeme konečný automat.
- Využití sufixové funkce $\sigma$ určující délku nejdelšího prefixu vzorku, který je sufixem slova.
- $\delta(q, a) = \sigma(P[1] ... P[q] a)$
- Tato metoda v $\mathcal{O}(m^3 \times \mid\Sigma\mid)$ .
  - Existuje procedura s $\mathcal{O}(m \times \mid\Sigma\mid)$ .
Text zpracujeme konečným automatem. $\Theta(n)$

KMP

Nekonstruujeme celý automat ale před vyhledáváním vypočteme prefixovou funkci pro vzorek.
- Postupně pro každou pozici ve vzorku určíme délku největšího podvzorku, který je zároveň prefixem i sufixem dosud zpracované části vzorku.
- $\mathcal{O}(m)$
Samotný výpočet pak probíhá obdobně jako naivní prohledávání, ale při neshodě (nebo nalezení vzorku) se:
- na textu nevracíme
- na vzorce posuneme na pole dle prefixové funkce
$\mathcal{O}(n)$

Boyer-Moore

Postupujeme zleva doprava a porovnáváme vzorek a text zprava.
Při neshodě můžeme využít dvě pravidla pro přeskočení pozic (vybereme větší skok):
- Heuristika špatného znaku
  - nejbližší další pozice znaku z textu ve vzorku
  - symbol se nevyskytuje ve vzorku ⇒ posun o i pozic
- Heuristika dobrého suffixu
  - najdeme nejpravější výskyt u = T[j+i+1…m-1], před kterým je symbol různý od a
    - ⇒ posun o i-r pozic (r = index znaku různého od a)
  - nenajdeme nejdelší řetězec v, který je současně prefixem i sufixem P
    - ⇒ posun vzorku o m-|v| pozic
Tabulky pro heuristiky si lze ze vzorku předpočítat před samotným výpočtem. $\mathcal{O}(m \times |\Sigma|)$
Vyhledávání $\mathcal{O}(m \times n)$ , ale očekávaně výrazně lepší.
- nejlepší případ: $\mathcal{O}(\frac{n}{m})$

Zdroje:

slidy IV003 (verze 2016)

mgr-szz/in-pos/2-pos.1560759675.txt.gz · Poslední úprava: 2020/04/12 16:56 (upraveno mimo DokuWiki)

Nahoru