Obsah
N-AP13
Zadání
Regulární jazyky. Konečné automaty, regulární gramatiky a regulární výrazy. Minimalizace konečného automatu. Převod nedeterministického konečného automatu na deterministický automat. Vztah mezi konečnými automaty a regulárními jazyky. Použití pumping lemmatu pro regulární jazyky.
Regulární jazyky
Abeceda je libovolná konečná množina, jejíž prvky se nazývají znaky. Abeceda může být i prázdná množina, zapisuje se Σ.
Slovo je libovolná konečná posloupnost znaků z abecedy.
Jazykem se rozumí libovolná množina slov nad nějakou abecedou. Jazyky mohou být konečné i nekonečné.
Regulární jazyk je jazyk generovatelný regulární gramatikou. Též je to jazyk rozpoznatelný konečným automatem nebo popsaný regulárním výrazem.
Vlastnosti regulárních jazyků
Popis vlastností regulárních jazyků je důležitý pro popis regulárních výrazů.
- Ø je regulární jazyk.
- { ε } je regulární jazyk.
- { a } je regulární jazyk.
Pokud jsou A a B regulární jazyky, pak sjednocení, průnik, rozdíl, zřetězení a iterace jsou regulární jazyky.
Pokud je A regulární jazyk, pak komplement A je regulární jazyk.
Pokud je A regulární jazyk, pak zrcadlový obraz jazyka A je regulární jazyk.
Všechny konečné jazyky jsou regulární.
Příklad: Iterace jazyka {„ab“, „c“}* je { ε, „ab“, „c“, „abab“, „abc“, „cab“, „cc“, „ababab“, … }
Jazyk L je regulární, právě když:
- může být vygenerován regulární gramatikou (tzn. existuje regulární gramatika G taková, že L(G) = L),
- je akceptovaný nějakým deterministickým konečným automatem (tzn. existuje deterministický konečný automat M takový, že L(M) = L),
- je akceptovaný nějakým nedeterministickým konečným automatem (tzn. existuje nedeterministický konečný automat M takový, že L(M) = L),
- může být popsán regulárním výrazem (tzn. existuje regulární výraz RE takový, že L(RE) = L)
Uzávěrové vlastnosti regulárních jazyků
Třída regulárních jazyků je uzavřena na:
- sjednocení (L1
L2),
- průnik (L1
L2),
- rozdíl (L1 \ L2),
- komplement (co–L),
- zřetězení (L1.L2)
- iteraci (L*),
- pozitivní iteraci (L+),
- zrcadlový obraz (reverzi) (LR)
Konečné automaty
Definice 2.1. 1)
- Q je neprázdná konečná množina stavů,
je konečná množina vstupních symbolů (vstupní abeceda),
: Q x
→ Q je parciální přechodová funkce (
: Q x
→ 2Q totální v případě nedeterministického konečného automatu),
- q0
Q je počáteční stav,
- F
Q je množina koncových stavů
Slovo akceptované automatem M je právě takové slovo, pod kterým automat přejde z počátečního stavu do koncového stavu.
Jazyk akceptovaný automatem M je množina všech slov, na kterých automat přejde z počátečního stavu do koncového stavu.
Rozšířená přechodová funkce deterministického konečného automatu:
Abychom mohli definovat jazyk akceptovaný automatem, je třeba zavést rozšířenou přechodovou funkci
: Q x
* → Q definována induktivně vzhledem k délce slova ze
*:
(q,
) = q pro každý stav q
Q
(q, wa) =
(
(q, w), a) je-li
(q, w) i
(
(q, w), a) definováno
jinak
Jazyk akceptovaný konečným automatem M, označovaný L(M) je tvořen právě všemi takovými slovy, pod kterými automat přejde z počátečního stavu do některého z koncových.
L(M) = {w * |
(q0,w)
F}
Rozšířená přechodová funkce nedeterministického konečného automatu:
: Q x
* → 2Q, definována induktivně vzhledem k délce slova ze
*:
(q,
) = {q}
(q, wa) =
Jazyk akceptovaný nedeterministickým konečným automatem M, označovaný L(M) je tvořen právě všemi takovými slovy, pod kterými automat přejde z počátečního stavu do některého z koncových.
L(M) = {w * |
(q0,w)
F
}
Regulární gramatiky
Definice 1.2. 2)
- N je neprázdná konečná množina neterminálních symbolů (neterminálů),
je konečná množina terminálních symbolů (terminálů) taková, že
;
je množina všech symbolů gramatiky,
- P
V*NV* x V* je konečná množina pravidel. Pravidlo
obvykle zapisujeme ve tvaru
(čteme „alfa přepiš na beta“),
- S
N je počáteční neterminál, neboli kořen gramatiky.
Gramatika je regulární, jestliže každé její pravidlo je tvaru A → aB (nebo A → Aa, tzv. levo lineární gramatika) nebo A → a s výjimkou S → , pokud se S nevyskytuje na pravé straně žádného pravidla.
Je to gramatika typu 3 podle Chomského hierarchie gramatik.
Regulární výrazy
Množina regulárních výrazů nad abecedou , označovaná RE(
), je definována induktivně takto:
,
a a pro každé a
jsou (základní) regulární výrazy nad
.
- Jsou-li E, F regulární výrazy nad
, jsou také (E.F), (E + F) a (E*) regulární výrazy nad
.
- Každý regulární výraz vznikne po konečném počtu aplikací kroků 1–2.
Závorky je možné vypouštět s tím, že největší prioritu má operátor „ * “, pak „ . “ a nakonec „ + “
Každý regulární výraz E nad abecedou popisuje jazyk L(E) nad abecedou
podle těchto pravidel:
- L(
) =
- L(
) =
- L(a) = {a} pro každé a
- L(E.F) = L(E).L(F)
- L(E+F) = L(E)
L(F)
- L(E*) = L(E)*
Regulární výrazy jsou tedy výrazy, které popisují množinu slov. Jsou ekvivalentní nějakému automatu případně gramatice. Využívají vlastností sjednoceni, průniku, rozdílu, iterace, zřetězení a komplementu. Lze napsat algoritmus, který rozhodne, zda jsou dva regulární výrazy ekvivalentní, tj. popisují stejný jazyk a redukovat daný jazyk na nějaký minimální automat.
Ekvivalenci mezi regulárními výrazy a konečnými automaty shrnuje Kleeneho veta:
Kleeneho věta
Minimalizace konečného automatu
Minimální automat je automat s nejmenším počtem stavů, který rozpoznává daný regulární jazyk L. Lze jej sestrojit z jakéhokoliv automatu rozpoznávající nějaký jazyk L.
Existence minimálního konečného automatu souvisí s Myhill–Nerodovou větou (viz otázka AP8,IN8 Regulární jazyky), kterou můžeme přeformulovat takto:
Věta 2.29 Myhill–Nerodova, 2. varianta3)
Důsledek M-N věty
Minimalizace konečného automatu probíhá tak, že nejprve jsou odstraněny nedosažitelné stavy a poté jsou ztotožněny jazykově ekvivalentní stavy.
Odstranění nedosažitelných stavů
Definice - dosažitelné a nedosažitelné stavy
Algoritmus pro eliminaci nedosažitelných stavů konečného automatu
Vstup: Konečný automat M = (Q, ,
, q0, F)
Výstup: Ekvivalentní automat M' bez nedosažitelných stavů.
Algoritmus
Si := {q0}
repeat Si+1 := Si
i := i + 1
until Si = Si–1 Q' := Si M' = (Q',
Poznámka: Zápis |Q' znamená, že funkce
je omezena na množinu Q'.
Intuitivně: Množina Si je množina stavů dosažitelná v automatu v maximálně i krocích.
Ztotožnění jazykově ekvivalentních stavů
Nechť M = (Q, ,
, q0, F) je konečný automat bez nedosažitelných stavů, jehož přechodová funkce je totální.
Definice - jazykově ekvivalentní stavy
p ≡ q
Definice - Redukt
- Stavy jsou třídy rozkladu Q/≡ (třída obsahující stav q je [q]).
- Přechodová funkce
je funkce splňující:
p,q
Q,
a
:
(q, a) = p
([q], a) = [p].
- Počáteční stav je třída rozkladu Q/≡ obsahující stav q0.
- Koncové stavy jsou právě ty třídy rozkladu Q/≡, které obsahují alespoň jeden koncový stav.
Věta
Definice
p ≡i q
- p ≡i q právě když p a q nelze „rozlišit“ žádným slovem délky
i
- p ≡ q právě když p ≡i q pro každé i
0. (≡ =
i)
- ≡0 = {(p, q) | p
F
q
F}
- ≡i+1 = {(p, q) | p ≡i q
a
:
(p, a) ≡i
(q, a)}
Algoritmus konstrukce minimálního automatu
Vstup: Konečný automat M = (Q, ,
, q0, F) bez nedosažitelných stavů s totální přechodovou funkcí
Výstup: Redukt M/≡.
Algoritmus
≡0 := {(p, q) | p
repeat ≡i+1 := {(p, q) | p ≡i q
i := i + 1
until ≡i = ≡i–1 ≡ = ≡i M/≡ := (Q/≡,
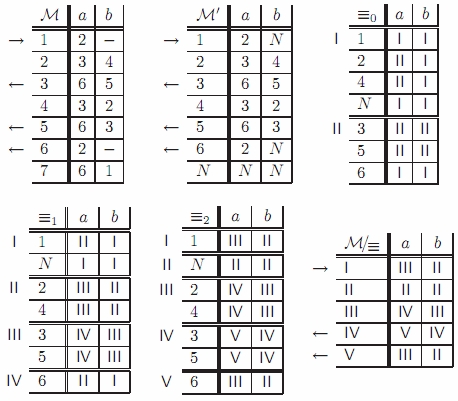
Příklad
- První tabulka obsahuje nedostupné stavy (stav 7).
- Druhá tabulka ukazuje přechodovou funkci po úpravě na totální, přidáním nového stavu N a nasměrováním všech nedefinovaných přechodů do něj.
- Ostatní čtyři tabulky reprezentují postupnou minimalizaci automatu.
Praktické vysvětlení algoritmu
Tabulku opět rozdělíme, do částí(tříd) které označíme římskými číslicemi, v každé necháme stavy ze kterých se pod všemi prvky abecedy dostaneme do stejných částí tabulky. Aplikujeme předchozí krok.(tabulka 4,5)
Tento postup aplikujeme dokud každá část tabulky neobsahuje jen stavy přecházející do stejných tříd. Ve výsledné tabulce nezapisujeme názvy stavů, ale jen označení tříd s jejich přechody(tabulka 6).
Převod nedeterministického automatu na deterministický
Věta
Nedeterministický konečný automat je definován stejne jako deterministický automat s tím rozdílem, že přechodová funkce se definuje jako totální zobrazení do množiny všech podmnožin stavů.
Jinými slovy z každého stavu může nedeterministický automat pod stejným vstupním symbolem přejít do různých stavů.
Obecně algortimus převodu vypadá tak, že:
1. Stavy nového automaty jsou z množiny všech podmnožin stavů Q.
2. Přechodová funkce je z množiny podmnožin do množiny podmnožin Q a na pravé straně přechodové funkce je množina všech stavů Q, kam by se NFA mohl dostat. V další iteraci je pak na pravé straně množina všech stavů, kam by se NFA mohl dostat ze všech stavů z podmnožiny z předchozí iterace.
3. Konečné stavy jsou pak ty, kde se v podmnožině vyskytuje alespoň jeden z koncových stavů z předchozího NFA.
Algoritmus transformace NFA na DFA
Vstup: NFA M = (Q, ,
, q0, F).
Výstup: Ekvivalentní DFA M' = (Q', ,
', {q0}, F') bez nedosažitelných stavů a s totální přechodovou funkcí.
Algoritmus
while (Q' – Done)
od M' = (Q',
Příklad
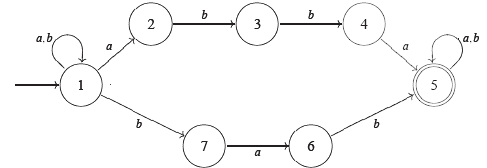
Mějme nedeterministický konečný automat :
| a | b | |
|---|---|---|
| → 1 | 1,2 | 1,7 |
| 2 | - | 3 |
| 3 | - | 4 |
| 4 | 5 | - |
| ← 5 | 5 | 5 |
| 6 | - | 5 |
| 7 | 6 | - |
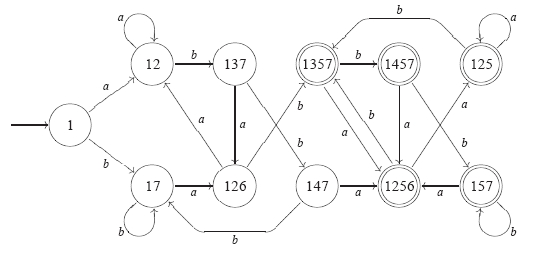
Převod nedeterministického automatu na deterministický provedeme pomocí algoritmu následovně:
Praktické vysvětlení algoritmu
Algoritmus končí, ve chvíli kdy není možné nalézt žádný nový stav. Vstupní stavy zůstávají stejné, koncové stavy jsou ty, které obsahují některý z původních koncových stavů.
Takto vytvořený automat nemusí být minimální, ale je bez nedosažitelných stavů, s totální přechodovou funkcí.
| a | b | |
|---|---|---|
| → 1 | 12 | 17 |
| 12 | 12 | 137 |
| 17 | 126 | 17 |
| 137 | 126 | 147 |
| 126 | 12 | 1357 |
| 147 | 1256 | 17 |
| ← 1357 | 1256 | 1457 |
| ← 1256 | 125 | 1357 |
| ← 1457 | 1256 | 157 |
| ← 125 | 125 | 1357 |
| ← 157 | 1256 | 157 |
Vztah mezi konečnými automaty a regulárními jazyky
Platí věta, že pro každý jazyk popsatelný nějakým regulárním výrazem existuje automat, který jej rozpoznává.
Dále platí věta, že pokud je jazyk rozponávaný nějakým DFA, pak je popsatelný regulráním výrazem.
Tj. obě třídy jazyku jsou ekvivalentní (Kleeneho věta).
Pumping Lemma pro regulární jazyky
Lemma 2.13. (o vkládání)4)
Je to prostředek jak dokázat, že nějaký daný jazyk není regulární. Představuje nutnou (nikoliv postačující) podmínku, kterou musí každý regulární jazyk splňovat.
Pumping lemma prakticky říká, že v dostatečně dlouhém slově w, které patří do jistého jazyka, lze nalézt tři části x, y a z, přičemž y může být i celé slovo. y lze pak libovolně opakovat (napumpovat), či zcela vyloučit a výsledné slovo bude patřit do jazyka. Délka slova musí být větší nebo rovna pumpovací konstantě n a délka části xy musí být menší nebo rovna n.
Postupujeme tak, že ukážeme, že pokud platí obměna lemmatu o vkládání (jde o implikaci), potom jazyk L není regulární:
- pro libovolné (všechna) n
(pumpovací konstanta)
- existuje takové w
L délky alespoň n, pro které platí, že
- při libovolném (všech) rozdělení slova w na tři části x, y, z, že |xy| ≤ n, y ≠
- existuje alespoň jedno i
0 takové, že xyiz
L
Potom z lemmatu o vkládání plyne, že L není regulární.
Intuitivní důkaz tvrzení říká:
• Pro konečné jazyky se jako pumpovací konstanta vezme délka nejdelšího slova.
• Pro nekonečné jazyky musí existovat nějaký minimální konečný automat, který je akceptuje. Spočítá se počet jeho stavů a vezme se jako pumpovací konstanta p. Pokud automat akceptuje i slova delší než p, pak musí některými stavy procházet vicekrát. Jeden tento stav označíme S. Transakce, které automat posunou ze stavu S, a zpět do stavu S, akceptují nějaký řetězec. Tento řetězec je y v pumping lemmatu, tj. platí tvrzení lemma, že lze slovo nafukovat i že lze nafukování přeskočit rovnou dál.
Předměty
IB102 Automaty a gramatiky
IB005 Formální jazyky a automaty
Vypracoval
Marek Menšík UČO 255679
Nevím přesně, kdo otázky zpracoval přede mnou, pouze jsem je sem umístil, doplnil chybějící věci a opravil nepřesnosti. Připomínám, že věci zde uvedené nemusí být korektní a zatím neprošly kontrolou žádného z profesorů. Z mé strany je tato otázka dokončena a případné chybějící věci a chyby mě můžete napsat na UČO mail nebo se registrujte a upravte je sami.