Obsah
AP8, IN8 Regulární jazyky
Zadání
regulární jazyky, způsoby jejich reprezentace, vlastnosti regulárních jazyků, vztah mezi konečnými automaty a regulárními gramatikami
Základní pojmy
Abeceda je libovolná konečná množina znaků (písmen, symbolů)
Slovo nad abecedou je libovolná konečná posloupnost znaků této abecedy
Jazyk nad abecedou je libovolná množina slov nad
Reprezentace regulárních jazyků
Jazyk L je regulární, právě když:
- může být vygenerován regulární gramatikou (tzn. existuje regulární gramatika G taková, že L(G) = L),
- je akceptovaný nějakým deterministickým konečným automatem (tzn. existuje deterministický konečný automat M takový, že L(M) = L),
- je akceptovaný nějakým nedeterministickým konečným automatem (tzn. existuje nedeterministický konečný automat M takový, že L(M) = L),
- může být popsán regulárním výrazem (tzn. existuje regulární výraz RE takový, že L(RE) = L)
Regulární gramatika
Definice 1.2. 1)
- N je neprázdná konečná množina neterminálních symbolů (neterminálů),
je konečná množina terminálních symbolů (terminálů) taková, že
;
je množina všech symbolů gramatiky,
- P
V*NV* x V* je konečná množina pravidel. Pravidlo
obvykle zapisujeme ve tvaru
(čteme „alfa přepiš na beta“),
- S
N je počáteční neterminál, neboli kořen gramatiky.
Gramatika je regulární, jestliže každé její pravidlo je tvaru A → aB nebo A → a s výjimkou S → , pokud se S nevyskytuje na pravé straně žádného pravidla.
Je to gramatika typu 3 podle Chomského hierarchie gramatik.
Konečný automat
Definice 2.1. 2)
- Q je neprázdná konečná množina stavů,
je konečná množina vstupních symbolů (vstupní abeceda),
: Q x
→ Q je parciální přechodová funkce (
: Q x
→ 2Q totální v případě nedeterministického konečného automatu),
- q0
Q je počáteční stav,
- F
Q je množina koncových stavů
Rozšířená přechodová funkce deterministického konečného automatu:
: Q x
* → Q definována induktivně vzhledem k délce slova ze
*:
(q,
) = q pro každý stav q
Q
(q, wa) =
(
(q, w), a) je-li
(q, w) i
(
(q, w), a) definováno
jinak
Rozšířená přechodová funkce nedeterministického konečného automatu:
: Q x
* → 2Q, definována induktivně vzhledem k délce slova ze
*:
(q,
) = {q}
(q, wa) =
Konečný automat je možné reprezentovat:
- uspořádanou pěticí
- tabulkou
- přechodovým grafem
- výpočetním stromem
více viz otázka AP9,IN9 Konečné automaty
Regulární výrazy
Množina regulárních výrazů nad abecedou , označovaná RE(
), je definována induktivně takto:
,
a a pro každé a
jsou (základní) regulární výrazy nad
.
- Jsou-li E, F regulární výrazy nad
, jsou také (E.F), (E + F) a (E*) regulární výrazy nad
.
- Každý regulární výraz vznikne po konečném počtu aplikací kroků 1–2.
Závorky je možné vypouštět s tím, že největší prioritu má operátor „ * “, pak „ . “ a nakonec „ + “
Každý regulární výraz E nad abecedou popisuje jazyk L(E) nad abecedou
podle těchto pravidel:
- L(
) =
- L(
) =
- L(a) = {a} pro každé a
- L(E.F) = L(E).L(F)
- L(E+F) = L(E)
L(F)
- L(E*) = L(E)*
Ekvivalenci mezi regulárními výrazy a konečnými automaty shrnuje Kleeneho veta:
Kleeneho věta
Lemma o vkládání (pumping lemma)
Lemma 2.13. (o vkládání)3)
Lemma o vkládání je nutnou (nikoliv postačující) podmínkou pro regularitu jazyka a lze jej použít pro důkaz toho, že nějaký jazyk není regulární (NE pro důkaz toho, že jazyk je regulární!!!). Postupujeme tak, že ukážeme, že pokud platí „negace“ lemmatu o vkládání, potom jazyk L není regulární:
- pro libovolné n
(pumpovací konstanta)
- existuje takové w
L, délky alespoň n, pro které platí, že
- při libovolném rozdělení slova w na tři části x, y, z, že |xy| ≤ n a y ≠
- existuje alespoň jedno i
0 takové, že xyiz
L
Potom z lemmatu o vkládání plyne, že L není regulární.
Myhill-Nerodova věta
Myhill-Nerodova věta představuje nutnou a postačující podmínku pro regularitu jazyka.
Pro formulaci M-N věty potřebujeme několik pomocných pojmů:
Definice – pravá kongruence
Definice – prefixová ekvivalence
u ~L v
Lemma
Věta 2.28 Myhill-Nerodova věta4)
- L je rozpoznatelný konečným automatem.
- L je sjednocením některých tříd rozkladu určeného pravou kongruencí na
* s konečným indexem.
- Relace ~L má konečný index.
Vlastnosti regulárních jazyků
Uzávěrové vlastnosti
Třída regulárních jazyků je uzavřena na:
- sjednocení (L1
L2),
- průnik (L1
L2),
- rozdíl (L1 \ L2),
- komplement (co–L),
- zřetězení (L1.L2)
- iteraci (L*),
- pozitivní iteraci (L+),
- zrcadlový obraz (reverzi) (LR)
Rozhodnutelné problémy pro třídu regulárních jazyků
Mějme konečné automaty M a M'.
Následující problémy jsou rozhodnutelné:
- ekvivalence: jsou M a M' ekvivalentní? (platí L(M)=L(M')?)
- inkluze (jazyků): platí L(M)
L(M')?
- příslušnost (slova k jazyku): je-li dáno w
*, platí w
L(M)?
- prázdnost (jazyka): je L(M) =
?
- univerzalita (jazyka): je L(M) =
*?
- konečnost (jazyka): je L(M) konečný jazyk?
Vztah mezi konečnými automaty a regulárními gramatikami
Třídy jazyků, které lze generovat regulárními gramatikami, resp. rozpoznat konečnými automaty, jsou si rovny. To znamená, že k dané regulární gramatice lze sestrojit ekvivalentní (deterministický, nedeterministický, …) konečný automat a naopak.
Regulární gramatika → konečný automat
Lemma 2.695)
(Důkaz viz skripta z Automatů a formálních jazyků I, str. 49)
Myšlenka důkazu:
Stavy automatu budou odpovídat neterminálům gramatiky, tj. pro každý neterminál A bude existovat stav . Pro každé pravidlo A → aB přidáme do
(
, a) stav
. Abychom se mohli vypořádat také s pravidly tvaru C → a, zavedeme speciální koncový stav qf, který přidáme do
(
, a). Počáteční stav bude
, koncový stav qf a případně také
, pokud gramatika obsahuje pravidlo S →
.
Konečný automat → regulární gramatika
Lemma 2.716)
(Důkaz viz skripta z Automatů a formálních jazyků I, str. 50)
Myšlenka důkazu:
Neterminály budou odpovídat stavům, pravidla budou simulovat přechodovou funkci. Je tu však jeden problém – pokud automat přijímá prázdné slovo (tj. počáteční stav je koncovým stavem), musí každá ekvivalentní gramatika nutně obsahovat pravidlo S → , kde S je kořen. Pak se ale S nesmí vyskytovat na pravé straně žádného pravidla. Přitom je ale možné, že některé přechody automatu končí v počátečním stavu a mají být simulovány pravidly, které mají na pravé straně S, což by vedlo ke konfliktu s požadavkem pravostranných výskytů S. Tento problém vyřešíme tak, že ke zkonstruované gramatice (mající jak S →
, tak i pravostranné výskyty S) nalezneme ekvivalentní regulární gramatiku.
Poznámka
Lingvista Noam Chomsky rozdělil gramatiky do čtyř skupin (typů) na základě různých omezení na tvar pravidel a podle jejich popisné síly.
Chomského hierarchie rozlišuje tyto čtyři (základní) typy gramatik:
- typ 0
Libovolná gramatika je gramatikou typu 0; na tvar pravidel se nekladou žádné omezující požadavky. Někdy též se takové gramatiky označují jako gramatiky bez omezení či frázové gramatiky.
- typ 1
Gramatika je typu 1 nebo též kontextová, jestliže pro každé její pravidlo platí platí
s eventuelní výjimkou pravidla
pokud se
nevyskytuje na pravé straně žádného pravidla.
- typ 2
Gramatika je typu 2, též bezkontextová, jestliže každé její pravidlo je tvaru , kde
s eventuelní výjimkou pravidla
pokud se
nevyskytuje na pravé straně žádného pravidla.
- typ 3
Gramatika je typu 3, též regulární, jestliže každé její pravidlo je tvaru nebo
s eventuelní výjimkou pravidla
, pokud se
nevyskytuje na pravé straně žádného pravidla.
Literatura
Vypracoval
Lukáš Hala, 173454@mail.muni.cz
Pokud si myslíte, že tady něco chybí, přebývá nebo že je něco blbě, tak to prosím upravte ![]()
 Je potřeba ještě zapracovat poznámky od Jitky Pospíšilové.
Je potřeba ještě zapracovat poznámky od Jitky Pospíšilové.


Diskuze
Doplnil som cast „Regularni vyrazy“ podla mna o dost dolezitu Kleeneho vetu a pravidla generovania jazyka z reg. vyrazov.
K pumping lematu - neni nahodou pumpovaci konstanta i? n je přece délka slova
Podle skript je jako pumpovací konstanta označeno n.
Je to pumpovaci _konstanta_, takze i to byt nemuze, to je cislo ktere se „pumpuje“
Neměla by tu být prefixová ekvivalence místo pravá kongruence??
(Třetí Lemma M-N věty)
Lemma: Nechť L je libovolný jazyk nad Sigma. Pak relace ~L je _pravá kongruence_ a L lze vyjádřit jako sjednocení některých (ne nutně konečně mnoha) tříd rozkladu Sigma*/~L.
Myslím, že ne. Prefixová ekvivalence (~L) je zároveň i pravou kongruencí(~) (důkaz je ve skriptech na straně 24 dole).
Ta Definice 1.2 není regulární gramatika ale obecná gramatika, regulární by měla mít množinu pravidel P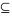 N x \Sigma*(N+ε)
N x \Sigma*(N+ε)