Obsah
AP9, IN9 Konečné automaty
Zadání
definice, konstrukce konečného automatu, minimalizace konečného automatu, převod nedeterministického konečného automatu na deterministický automat
Definice konečného automatu
Definice 2.1. 1)
- Q je neprázdná konečná množina stavů,
je konečná množina vstupních symbolů (vstupní abeceda),
: Q x
→ Q je parciální přechodová funkce (v případě nedeterministického konečného automatu je definována jako totální zobrazení
: Q x
→ 2Q),
- q0
Q je počáteční stav,
- F
Q je množina koncových stavů
Rozšířená přechodová funkce deterministického konečného automatu:
Abychom mohli definovat jazyk akceptovaný automatem, je třeba zavézt rozšířenou přechodovou funkci
: Q x
* → Q definována induktivně vzhledem k délce slova ze
*:
(q,
) = q pro každý stav q
Q
(q, wa) =
(
(q, w), a) je-li
(q, w) i
(
(q, w), a) definováno
jinak
Jazyk akceptovaný konečným automatem M, označovaný L(M) je tvořen právě všemi takovými slovy, pod kterými automat přejde z počátečního stavu do některého z koncových.
L(M) = {w * |
(q0,w)
F}
Rozšířená přechodová funkce nedeterministického konečného automatu:
: Q x
* → 2Q, definována induktivně vzhledem k délce slova ze
*:
(q,
) = {q}
(q, wa) =
Jazyk akceptovaný nedeterministickým konečným automatem M, označovaný L(M) je tvořen právě všemi takovými slovy, pod kterými automat přejde z počátečního stavu do některého z koncových.
L(M) = {w * |
(q0,w)
F
}
Konstrukce konečného automatu
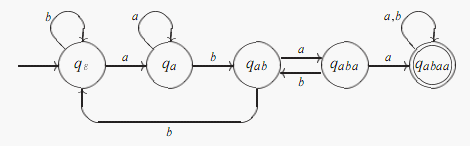
Mějme například jazyk L = {w {a, b}* | w obsahuje podslovo abaa}.
- konstrukce konečného automatu, který rozpoznává daný jazyk, je obecně netriviální úkol. Pro zjednodušení proto volíme označení stavů tak, aby bylo patrné, jaká část podslova abaa již byla automatem přečtena.
Konečný automat akceptující jazyk L je možné reprezentovat:
Uspořádanou pěticí
kde přechodová funkce
vypadá následovně:
| | |
| | |
| | |
| | |
| | |
Tabulkou
| a | b | ||
|---|---|---|---|
| → | | | |
| | | |
|
| | | |
|
| | | |
|
| ← | | | |
Přechodovým grafem
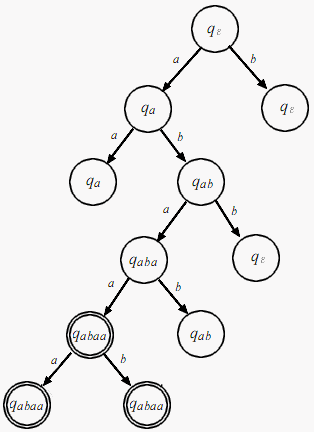
Výpočetním stromem
- není určen jednoznačně. Může se lišit podle toho, jakým způsobem jej konstruujeme.
- Příklad výpočetního stromu pro automat M:
Synchronní paralelní kompozice
Pro dané automaty M1 a M2 umožňuje sestrojit automat rozpoznávající průnik, sjednocení či rozdíl jazyků L(M1) a L(M2).
Nechť M1 = (Q1, ,
1, q1, F1), M2 = (Q2,
,
2, q2, F2) a přechodové funkce
1,
2 jsou totální.
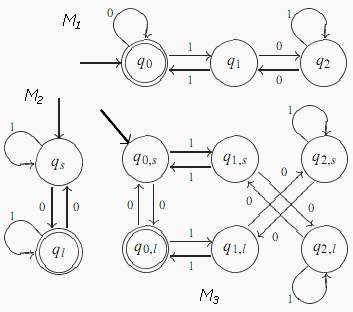
Definujeme konečný automat M3 = (Q3, ,
3, q3, F3), kde
- Q3 = Q1 x Q2 = {(p,q) | p
Q1, q
Q2}
- F3 = F1 x F2 = {(p,q) | p
F1, q
F2}
- q3 = (q1, q2)
3( (p,q),a) = (
1(p,a),
2(q,a) )
Potom L(M3) = L(M1) L(M2)
Podobně pro sjednocení a rozdíl - zmení sa len množina koncových stavov
- F3 = (F1 x Q2)
(Q1 x F2) = {(p,q) | p
F1 ∨ q
F2} pre zjednotenie
- F3 = F1 - F2 = {(p,q) | p
F1 ∧ q
F2} pre rozdiel
Příklad průniku
Automat pro komplement
K automatu M = (Q, ,
, q0, F) s totální přechodovou funkcí sestrojíme automat
rozpoznávající jazyk co–L(M) jako
= (Q,
,
, q0, Q – F).
Poznámka: přechodovou funkci ztotálníme tak, že přidáme nový nekoncový stav („černá díra“), do kterého „nasměrujeme chybějící šipky“.
Minimalizace konečného automatu
Minimální konečný automat = automat s nejmenším počtem stavů, který rozpoznává daný regulární jazyk L.
Existence minimálního konečného automatu souvisí s Myhill–Nerodovou větou (viz otázka AP8,IN8 Regulární jazyky), kterou můžeme přeformulovat takto:
Věta 2.29 Myhill–Nerodova, 2. varianta2)
Důsledek M-N věty
Minimalizace konečného automatu probíhá tak, že nejprve jsou odstraněny nedosažitelné stavy a poté jsou ztotožněny jazykově ekvivalentní stavy.
Odstranění nedosažitelných stavů
Definice - dosažitelné a nedosažitelné stavy
Algoritmus pro eliminaci nedosažitelných stavů konečného automatu
Vstup: Konečný automat M = (Q, ,
, q0, F)
Výstup: Ekvivalentní automat M' bez nedosažitelných stavů.
Algoritmus
Si := {q0}
repeat Si+1 := Si
i := i + 1
until Si = Si–1 Q' := Si M' = (Q',
Poznámka: Zápis |Q' znamená, že funkce
je omezena na množinu Q'.
Intuitivně: Množina Si je množina stavů dosažitelná v automatu v maximálně i krocích.
Ztotožnění jazykově ekvivalentních stavů
Nechť M = (Q, ,
, q0, F) je konečný automat bez nedosažitelných stavů, jehož přechodová funkce je totální.
Definice - jazykově ekvivalentní stavy
p ≡ q
Definice - Redukt
- Stavy jsou třídy rozkladu Q/≡ (třída obsahující stav q je [q]).
- Přechodová funkce
je funkce splňující:
p,q
Q,
a
:
(q, a) = p
([q], a) = [p].
- Počáteční stav je třída rozkladu Q/≡ obsahující stav q0.
- Koncové stavy jsou právě ty třídy rozkladu Q/≡, které obsahují alespoň jeden koncový stav.
Věta
Definice
p ≡i q
- p ≡i q právě když p a q nelze „rozlišit“ žádným slovem délky
i
- p ≡ q právě když p ≡i q pro každé i
0. (≡ =
i)
- ≡0 = {(p, q) | p
F
q
F}
- ≡i+1 = {(p, q) | p ≡i q
a
:
(p, a) ≡i
(q, a)}
Algoritmus konstrukce minimálního automatu
Vstup: Konečný automat M = (Q, ,
, q0, F) bez nedosažitelných stavů s totální přechodovou funkcí
Výstup: Redukt M/≡.
Algoritmus
≡0 := {(p, q) | p
repeat ≡i+1 := {(p, q) | p ≡i q
i := i + 1
until ≡i = ≡i–1 ≡ = ≡i M/≡ := (Q/≡,
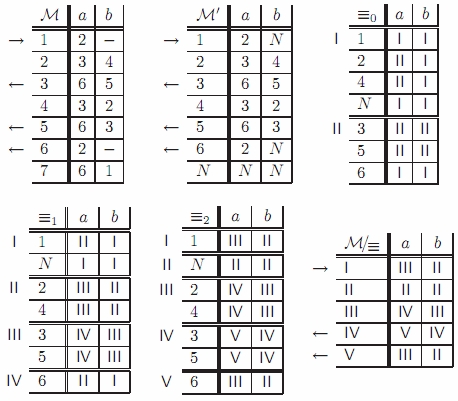
Příklad
- První tabulka obsahuje nedostupné stavy (stav 7).
- Druhá tabulka ukazuje přechodovou funkci po úpravě na totální, přidáním nového stavu N a nasměrováním všech nedefinovaných přechodů do něj.
- Ostatní čtyři tabulky reprezentují postupnou minimalizaci automatu.
Praktické vysvětlení algoritmu
Tabulku opět rozdělíme, do částí(tříd) které označíme římskými číslicemi, v každé necháme stavy ze kterých se pod všemi prvky abecedy dostaneme do stejných částí tabulky. Aplikujeme předchozí krok.(tabulka 4,5)
Tento postup aplikujeme dokud každá část tabulky neobsahuje jen stavy přecházející do stejných tříd. Ve výsledné tabulce nezapisujeme názvy stavů, ale jen označení tříd s jejich přechody(tabulka 6).
Převod NFA na DFA
Věta
Algoritmus transformace NFA na DFA
Vstup: NFA M = (Q, ,
, q0, F).
Výstup: Ekvivalentní DFA M' = (Q', ,
', {q0}, F') bez nedosažitelných stavů a s totální přechodovou funkcí.
Algoritmus
while (Q' – Done)
od M' = (Q',
Příklad
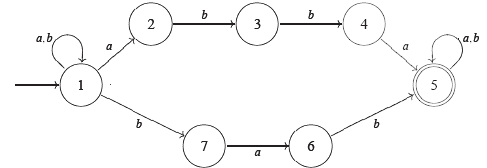
Mějme nedeterministický konečný automat :
| a | b | |
|---|---|---|
| → 1 | 1,2 | 1,7 |
| 2 | - | 3 |
| 3 | - | 4 |
| 4 | 5 | - |
| ← 5 | 5 | 5 |
| 6 | - | 5 |
| 7 | 6 | - |
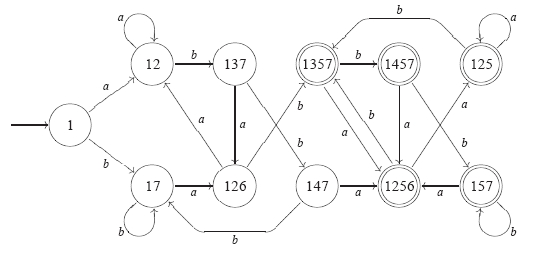
Převod nedeterministického automatu na deterministický provedeme pomocí algoritmu následovně:
Praktické vysvětlení algoritmu
Algoritmus končí, ve chvíli kdy není možné nalézt žádný nový stav. Vstupní stavy zůstávají stejné, koncové stavy jsou ty, které obsahují některý z původních koncových stavů.
Takto vytvořený automat nemusí být minimální, ale je bez nedosažitelných stavů, s totální přechodovou funkcí.
| a | b | |
|---|---|---|
| → 1 | 12 | 17 |
| 12 | 12 | 137 |
| 17 | 126 | 17 |
| 137 | 126 | 147 |
| 126 | 12 | 1357 |
| 147 | 1256 | 17 |
| ← 1357 | 1256 | 1457 |
| ← 1256 | 125 | 1357 |
| ← 1457 | 1256 | 157 |
| ← 125 | 125 | 1357 |
| ← 157 | 1256 | 157 |
Využití
Konečné automaty se používají např. k lexikální analýze.
Literatura
Vypracoval
Lukáš Hala, 173454@mail.muni.cz
Pokud si myslíte, že tady něco chybí, přebývá nebo že je něco blbě, tak to prosím upravte ![]()
 Je potřeba ještě zapracovat poznámky od Jitky Pospíšilové.
Je potřeba ještě zapracovat poznámky od Jitky Pospíšilové.


Diskuze
Ahoj, bylo by dobre, dat obrazky sem na wiki, ted se tahaji od tebe z webu, v budoucnu by pak mohli chybet.
done
Ok.
A díky za doplnění příkladu a praktických vysvětlení algoritmů
Nemyslím, že výpočetní strom je vhodná reprezentace automatu. Spíš reprezentuje výpočet automatu nad daným slovem.
Podle mě nereprezentuje jenom výpočet nad daným slovem, ale nad jakýmkoliv slovem z jazyka. Například když dojdu po slově abb do stavu qe, tak můžu pokračovat zase od kořene qe (nebo od kteréhokoliv jiného stavu qe).
A když spojíš stejně pojmenované stavy, tak dostaneš přechodový graf. Na původním obrázku mi chyběli dva spodní koncové stavy, tak to asi bylo trochu matoucí. Teď už je to snad jasnější.
A že můžeme konečný automat reprezentovat výpočetní stavem potvrzují i skripta na straně 12.
(kdybych náhodou psal nesmysly, tak mě někdo opravte )
)
Ahoj, v casti o minimalizacii, pri definicii reduktu je uvedene, ze stavy su triedy rozkladu <em>M</em>/≡, ma tam byt zrejme Q namiesto M…
Díky, opraveno.
Myslím si, že v definici 2.1 je slovo totální v zavádějícím kontextu. Takhle to vypadá, jako by Q x Sigma → Q byla parciální a Q x Sigma → 2^Q byla totální a přitom imho je rozdíl v tom, jestli má nebo nemá definovanou hodnotu pro každý parametr. To jestli má obor hodnot Q nebo 2^Q rozlišuje imho jen DFA od NFA…
Jinak řečeno parciální je třeba pro FA ({q0,q1},{a,b},delta,q0,{q1}) delta definovaná jako d(q0,a)=q1, zatímco totální by byla třeba: d(q0,a)=q1,d(q0,b)=qx,d(q1,a)=qx,d(q1,b)=qx a qx by se přidal jako nový stav „černá díra“. A v obou případech by to byl DFA a navíc by byly ekvivalentní.
Pletu se nebo je to tak ? Díky
? Díky  .
.
Jo, je to tak. Trochu jsem to přepsal, aby to nebylo zavádějící
Při převodu NFA na DFA jsou koncové stavy všechy, které vznikly sjednocením množiny stavů ve které byl aspoň jeden stav koncový?
viz prakticke vysvetleni algoritmu: „Algoritmus končí, ve chvíli kdy není možné nalézt žádný nový stav. Vstupní stavy zůstávají stejné, koncové stavy jsou ty, které obsahují některý z původních koncových stavů.“
jestli to jeste nekdo cte, tak me se u statnic zeptal p. Strejcek na redukci epsilon pravidel