Obsah

AP2, IN2 Elementární kombinatorika
Diskuze

AP2, IN2 Elementární kombinatorika

(variace, kombinace a permutace)

Vypracovanie

Variácie

Nech S je konečná množina. Variácie definujeme ako usporiadané (t.j záleží na poradí prvkov) výbery prvkov množiny S. Rozlišujeme ich podľa toho, či sa prvky z S v týchto výberoch môžu alebo nemôžu opakovať.

Variácie

Počet variácií k-tej triedy z n prvkov je:

bez opakovania $V_{k}(n) = \frac{n!}{(n-k)!}$
s opakovaním $n^{k}$

Variácie s opakovaním k-tej triedy z n prvkov jsou uspořádané k-tice vybrané z n prvků. Môžeme je chápať aj ako množinu všetkých zobrazení k-prvkovej množiny X (X je ľubovoľná množina obsahujúca k prvkov) do n-prvkovej množiny S. Variácie bez opakovania sú teda všetky prosté zobrazenia $X \rightarrow S$ .

Variácie bez opakovania

Zadanie: Na turnaj nastúpilo 16 mužstiev. Koľko je možností obsadenia prvých 3 priečok?
Riešenie: Záleží na poradí mužstiev, ide teda o variácie 3. triedy zo 16 prvkov: $V_{3}(16) = \frac{16!}{(16-3)!} = 16\cdot 15\cdot 14$

Variácie s opakovaním

Zadanie: Koľkými spôsobmi môžeme zakódovať zámok na bicykel, ak je kód trojmiestny?
Riešenie: Prvé číslo môžeme vyberať z číslic 0, 1, …, 9, druhé a tretie tak isto. Takže variácie 3-tej triedy z 10 prvkov a môžu sa opakovať: $V'_{3}(10) = 10^{3} = 1000$

Permutácie

Permutácia n prvkov je skupina všetkých n prvkov, ktoré sú usporiadané v nějakém fixním poradí, tzn. výber prvkov závisí na poradí. Je to vlastně speciální případ variace bez opakování n-té třídy z n prvků. Rozlišujeme permutácie bez opakovania a s opakovaním. Permutáciu môžeme chápať aj ako bijektívne zobrazenie $S \rightarrow S$ (S je konečná množina).

Permutácie bez opakování

Počet všetkých permutácií n prvkovej množiny vypočítame:

ak sa prvky v množine neopakujú:

$P(n) = V_{n}(n) = \frac{n!}{(n-n)!} = n!$ (permutácie n prvkovej množiny bez opakovania sú vlastne variácie n-tej triedy z n prvkov)

Príklad na permutácie bez opakovania

Zadanie: Koľkými spôsobmi sa dajú postaviť do rady 4 Angličani, 5 Francúzi a 3 Turci, ak osoby tej istej národnosti musia stáť vedľa seba?
Riešenie: Máme 3 skupiny (počet permutácií skupín - 3!) a v rámci každej skupiny chceme rôzne zoradiť ľudí tej istej národnosti - permutácie bez opakovania:
$3! \cdot 4! \cdot 5! \cdot 3!$

Permutace s opakováním

Pokud se prvky ve výběru mohou opakovat, pak počet permutací s opakováním je určen jako
$P(n_1,n_2,...,n_k) = \frac{(n_1+n_2+...+n_k)!}{n_1!\cdot n_2!\cdot ... \cdot n_k!} = \frac{n!}{n_1!\cdot n_2!\cdot ... \cdot n_k!}$ – přičemž mezi vybranými prvky je k skupin, které mají postupně $n_{1},n_{2},...,n_{k}$ stejných prvků. Musí přitom platit $n = \sum_{i=1}^{k} n_{i}$ . ¹⁾

Príklad na permutácie s opakovaním

Zadanie: Určte počet všetkých anagramov, ktoré sa dajú zostaviť z písmen slova ABRAKADABRA.
Riešenie: Jedná sa o permutácie s opakovaním, pretože niektoré písmená sa vyskytujú v slove viac ako 1x. Písmeno A sa vyskytuje 5x, R 2x, K 1x, B 2x, D 1x, výsledný počet anagramov teda je:
$\frac{(5+2+1+2+1)!}{5! \cdot 2! \cdot 1! \cdot 2! \cdot 1!}$

Grupa permutácií

Nech X je množina. Ak množinu všetkých permutácií na množině X označíme S(X) a $\circ$ operáciu skladania zobrazenia, $(S(X),\circ)$ je nekomutatívna grupa.
Neformálny dôkaz: $\circ$ je operácia na S(X), je asociatívna, neutrálny prvok je identická permutace a keďže permutácia je bijektívne zobrazenie, vždy existuje inverzný prvok (zobrazenie).

Permutácie môžeme zapísať rôznymi spôsobmi:

tabuľkou, kde v hornom riadku je vstupná hodnota funkcie a v dolnom riadku výsledná hodnota: $f = \begin{pmatrix}1 & 2 & 3 & 4 & 5 & 6 \\ 3 & 1 & 5 & 2 & 4 &6\end{pmatrix}$

ako zloženie cyklov a transpozíc (cyklov dĺžky 2): $f = (1,3,5,4,2) = (1,3) \circ (3,5,4,2) = (1,3) \circ (3,5) \circ (5,4) \circ (4,2)$ (identickú permutáciu v rozklade neuvádzame)

Veta 1.1

Každá permutácia množiny $\{1,...,n\}$ , kde $n > 1$ je súčin transpozíc. Identická permutace je súčin $(i,j)\circ(i,j)$ , kde i,j sú ľubovoľné navzájom rôzne prvky z $\{1,...,n\}$ .

Vlastnosti permutácií

Permutácia je sudá (lichá), ak sa dá rozložiť na sudý (lichý) počet transpozíc. Permutácia uvedená vyššie je teda sudá. Rozklad na transpozície nie je určený jednoznačne (napr. permutácia $(1,2,3) = (1,2)\circ(2,3)$ , ale aj $(1,2,3) = (1,3)\circ(1,2)$ ), jednoznačne je určená len parita permutácie.

Parita $p(f)=1$ ak permutácia f je sudá, ak je permutácia f lichá, $p(f)=-1$ .

Cyklus $(r,r),\ r \in X$ nie? je transpozícia, pretože sa jedná o cyklus dĺžky 1. Pri určovaní parity sa teda nebere do úvahy. Z toho bezprostredne vyplýva, že identická permutace je sudá - dá sa rozložiť na 0 transpozícií. Vo všeobecnosti platí:
cyklus dĺžky n sa dá rozložiť na n-1 transpozíc

Každý prvok $r \in X$ , pre ktorý platí $f(r) = r,\ f \in S(X)$ , se nazývá samodružným prvkom (v rozklade na transpozície ho neuvádzame, jedná sa o transpozíciu? (r,r)). Ak je každý prvok permutace samodružný, hovoríme o identickej permutácii.

Ak máme permutáciu $f,\ f^{k}$ značí permutáciu, ktorá vznikne k-násobným zložením permutácie $f$ , tj. $\ f^1 = f$ , $f^k = f \circ f^{k-1}$ .

Rád permutácie je nejmenšie prirodzené číslo k také, pre ktoré platí $\ f^k = I$ , tj. po k zloženiach vznikne identická permutácia.

Inverzná permutácia

K permutácii
$f = \begin{pmatrix}a_1 & a_2 & ... & a_n \\ b_1 & b_2 & ... & b_n\end{pmatrix}$

je možné vytvoriť inverznú permutáciu:

$f^{-1} = \begin{pmatrix}b_1 & b_2 & ... & b_n \\ a_1 & a_2 & ... & a_n\end{pmatrix}$

Zložením permutácie f a k nej inverznej permutácii f^-1 získame identickú permutáciu.

Skladanie permutací

Majme na množine X dve permutácie:

$f_1 = \begin{pmatrix}a_1 & a_2 & ... & a_n \\ b_1 & b_2 & ... & b_n\end{pmatrix}$

$f_2 = \begin{pmatrix}b_1 & b_2 & ... & b_n \\ c_1 & c_2 & ... & c_n\end{pmatrix}$

Zložením permutácií $f_1, f_2$ je permutácia

$f = f_2 \circ f_1 = \begin{pmatrix}a_1 & a_2 & ... & a_n \\ c_1 & c_2 & ... & c_n\end{pmatrix}$

Operácia zloženia permutácií nie je komutatívna, ak má množina X aspoň 3 prvky.

Kombinácie

Nech S je konečná množina. Kombinácie sú neusporiadané výbery prvkov (t.j. nezáleží na ich poradí) množiny S. Opäť rozlišujeme kombinácie s opakovaním a bez opakovania. Každá kombinácia k-tej triedy bez opakování určuje k! variácií, preto môžeme vzorec na výpočet kombinácií odvodiť zo vzorcu na výpočet variácií.
Pro kombinace s opakováním se vzorec odvodí metodou přepážek a kuliček.

Kombinácie

Počet kombinácií k-tej triedy z n prvkov ( $k \leq n$ ) sa rovná:

bez opakovania $C_k(n) = {n \choose k} = \frac{n!}{(n-k)!\cdot k!}$

s opakovaním $C'_k(n) = {n+k-1 \choose k}$

Čísla ${n \choose k}$ sa nazývajú kombinačné čísla. Platia pre ne nasledujúce vzťahy:

${n \choose k} = {n \choose n-k}$

$\sum_{k=0}^n {n \choose k} = 2^n$

${n+1 \choose k} = {n \choose k} + {n \choose k-1}$

${n \choose 0} = 1$

${n \choose n} = 1$

Tretí vzťah súvisí s Pascalovým trojuholníkom, ktorý je geometrickou reprezentáciou binomických koeficientov: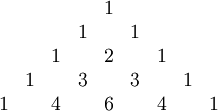
V 2.riadku Pascalovho trojuholníka (číslujeme od 0) sú čísla ${2 \choose 0},\ {2 \choose 1}$ a ${2 \choose 2}$ , sčítaním ${2 \choose 1}$ a ${2 \choose 2}$ dostaneme číslo pod nimi ${3 \choose 2} = 3$ . Pascalov trojuholník vyjadruje koeficienty v binomickom rozvoji podľa binomickej vety:

Binomická veta

Pre ľubovoľné $x,y \in C$ a $n \geq 0$ platí:
$(x+y)^n = \sum_{k=0}^n {n \choose k}\cdot x^{n-k}\cdot y^k$

n-tý riadok v Pascalovom trojuholníku určuje koeficienty binomického rozvoja $(x+y)^n$ , teda napr. pre $n=3$ :
$(x+y)^3 = x^3 + 3x^2 y + 3xy^2 + y^3$

Príklad na kombinácie

Zadanie: Koľkými spôsobmi sa dajú vybrať z čísel 1, 2, 3,..,29, 30 tri čísla tak, aby ich súčet bol sudý?
Riešenie: Súčet 3 čísel je sudý, ak sčítancami sú 2 liché a jedno sudé alebo 3 sudé čísla. V uvedenej číselnej rade je 15 sudých a 15 lichých čísel. Výsledný počet teda je:
${15 \choose 2}\cdot {15 \choose 1} + {15 \choose 3}$

Kombinácie s opakovaním

Zadanie: V cukrárni sa podávajú 4 druhy zákuskov :
venček, veterník, laskonky a doboška. Koľkými spôsobmi sa dá kúpit 7 zákuskov?
Riešenie: Kombinácie 7-mej triedy, vyberáme zo 4 prvkov, ktoré sa môžu opakovať: $C'_7(4) = {4+7-1 \choose 7}$

Kombinácie bez opakovania

Zadanie: Na vecierku sa stretne 5 priatelov. Každý si podá
ruku so všetkými ostatnými. Kolko bolo medzi týmito priateľmi podaní rúk?
Riešenie: 2-členné kombinácie z 5 prvkov bez opakovania: $C_2(5) = {5 \choose 2} = \frac{5!}{(5-2)!\cdot 2!} = 10$

Princípy použiteľné pri riešení kombinatorických úloh

Princíp súčtu

$A = A_1 \cup A_2 \cup \ldots \cup A_k$
používa sa tam, kde sa rôzne varianty spočítavajú, navzájom sa neovplyvňujú

Príklad na princíp súčtu

Zadanie: V triede je 30 žiakov. Koľko môžeme vytvoriť rôznych dvoj- alebo trojčlenných skupiniek?
Riešenie: Vypočítame, koľko môžeme vytvoriť dvojčlenných skupiniek (tých je ${30 \choose 2}$ ) a trojčlenných ( ${30 \choose 3}$ ) a tieto čísla potom iba spočítame. Výsledok je ${30 \choose 2} + {30 \choose 3}$ .

Princíp súčinu

$A = A_1 \times A_2 \times \ldots \times A_k$
používa sa tam, kde výsledok je súčin jednotlivých variánt, kde varianty spolu úzko súvisia
platí: $|A| = |A_1| \cdot |A_2| \cdot \ldots \cdot |A_k|$

Príklad na princíp súčinu

Zadanie: V triede je 30 žiakov, z toho 18 chlapcov a 12 dievčat. Koľko rôznych päťčlenných skupiniek takých, že 2 členovia skupinky budú chlapci a 3 dievčatá, môžeme vytvoriť?
Riešenie: Vyberáme 2 chlapcov z 18 (takže ${18 \choose 2}$ ) a 3 dievčatá z 12 ( ${12 \choose 3}$ ). Avšak dvojčlenná skupinka chlapcov môže vytvoriť päťčlennú skupinku s ktoroukoľvek možnou trojčlennou skupinkou dievčat, takže tieto dva kombinačné výbery musíme vynásobiť. Výsledok teda bude ${18 \choose 2} \times {12 \choose 3}$ .

Ak si nechcete pamätať alebo vymýšľať 2 nové príklady, posledný príklad na kombinácie v sebe spája princíp súčtu, aj princíp súčinu.

Princíp inklúzie a exklúzie

popisuje spôsob ako môžeme zistiť počet prvkov zjednotenia dvoch alebo viacerých množín

Príklad na princíp inklúzie a exklúzie

Zadanie:

Množiny A, B, C s neprázdným spoločným prienikom

Aký je počet prvkov zjednotenia množín A, B a C?
Riešenie: $|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |A \cap C| + |A \cap B \cap C|$

Všeobecný vzorec princípu inklúzie a exklúzie ²⁾

$\left|\bigcup_{i=1}^n A_i\right|=\sum_{i=1}^n\left|A_i\right| -\sum_{i,j\,:\,i<j}\left|A_i\cap A_j\right|+\sum_{i,j,k\,:\,i< j< k}\left|A_i\cap A_j\cap A_k\right|-\ \cdots$

$\cdots\ +(-1)^{(n-1)} \left|A_1\cap\cdots\cap A_n\right| =\\ \sum_{k=1}^n\sum_{1\leq i_1<\ldots <i_k\leq n}(-1)^{k+1}|A_{i_1}\cap\cdots\cap A_{i_k}|$

Predmety

FI:MB005 Základy matematiky (podzim 2005), Mgr. Ondřej Klíma, Ph.D.
FI:MB008 Algebra I (podzim 2006), doc. RNDr. Libor Polák, CSc.

Použitá literatúra

Učebné materiály k MB005
Permutace, Wikipedia
Princíp zapojenia a vypojenia, SK Wikipédia
Jiří Rosický: Algebra, ISBN 80-210-2964-1, Brno 2005

Vypracoval

Dušan Katona, ICQ: 426 081 873, snad do 30.5
hotovo: <99%>
môžete kluďne niečo doplniť alebo opraviť

Otázku si přečetl pan RNDr. Jan Bouda a rámcově prošel mimo části „Princípy použiteľné pri riešení kombinatorických úloh“, která byla dodána do otázky až po kontrole. Jeho podněty pro doplnění textu, opravy nesrovnalostí a odstranění matoucích či k otázce se nevztahujících textů byly do otázky zaneseny. Tato kontrola je jen rámcová, stále se může stát, že v otázce zůstala zapomenutá chybka či nesrovnalost, vyučující za toto nenese odpovědnost, berte tuto rámcovou kontrolu jako formu pomoci od vyučujících pro studenty.

¹⁾

prevzato z http://cs.wikipedia.org/wiki/Permutace

²⁾

prevzaté z: Princíp zapojenia a vypojenia - SK Wikipédia

Diskuze

Dusan Katona, 2008/05/29 19:00

Do otazky som nezahrnul „Princip inkluze a exkluze“, lebo som to nepovazoval za nutne…Ak si myslite opak, dajte mi vediet, doplnim to. Myslite si, ze Pascalov trojuholnik a binomicku vetu je vhodne spomenut v tejto otazke?
Ak najdete nejake vhodnejsie priklady na variacie, permutacie alebo kombinacie, mozete ich sem pridat, pripadne nahradit stavajuce priklady.

JK, 2008/06/02 09:41

Asi bych doplnil, ze binomicka veta plati pro kazda komplexni cisla x,y a kazde prirozene cislo n…

Dusan Katona, 2008/06/03 20:44

doplnene :)

Tomáš Gazárek, 2008/06/04 13:02

U rozkladu na transpozice f=(1,3,5,4,2)o(6,6) mame s kamosem za to, ze tam ma byt jen (6), nechapeme proc je tam (6,6).
A u prikladu vlastnosti permutaci (1,2,3) = (1,2)o(2,3), ale aj (1,2,3) = (1,3)o(1,2)← nema tu byt (3,1)o(1,2) ??

Nemate nekdo nejake vysvetleni?

Milan Kabát, 2008/06/08 23:09

Podľa mňa tam nemá byť ani (6), pretože nižšie uvedená definícia hovorí, že 6 je samodružným prvkom a v rozklade na transpozície sa neuvádza. Teda i parita uvedenej permutácie by mala byť párna (sudá).

Opravte ma prosím ak sa mýlim.

Michal Bednář, 2008/06/04 13:08

Neni nahodou identicka transpozice (i,i)?

Michal Bednář, 2008/06/04 13:11

tak sorry..mas pravdu..nasle jsem to ted ve skriptech..identicka permutace je opravdu (i,j)(j,i)

Michal Bednář, 2008/06/04 13:18

Pri skladani permutaci se sklada zprava. Takze kdyz f1°f2, tak se nejprve provede permutace f2, pak f1. Takze v tom uvedenem prikladu je ten vysledek vysledkem slozeni f2°f1 (rika se take f2 po f1).

Jan Palas, 2008/06/08 09:59

Ahoj, měl bych otázku ohledně parity permutací. V části vlastnosti permutací je uvedeno, že transpozice ve tvaru (r,r) se v rozkladu na transpozice neuvádějí. Nicméně v příkladu o kousek výše taková transpozice uvedena je a to (6,6). Není mi jasné, jak je to v tomto případě s paritou permutace. Zda se transpozice tvaru (r,r) berou při počítání parity v úvahu či nikoliv. Předem díky za osvětlení…

Dusan Katona, 2008/06/09 00:31

zda sa, ze si nasiel chybu :) transpozicia je cyklus dlzky 2, co identicka permutacia (r,r) nie je…opravim to, dik

Michal Bednář, 2008/06/12 22:03

Identické permutace se při zápisu cyklů vynechávájí a jsou sudé. Správně je f = (1,3,5,4,2) = (1,3)(3,5)(5,4)(4,2). Cyklus je lichý (parita -1), pokud má sudou délku → permutace (1,2,3,4) nebo (1,2) jsou liché. Transpozice je tedy lichá a má paritu -1. Z toho plyne, že permutace je sudá právě když se dá rozložit na sudý počet (lichých) transpozic (-1 * -1 = 1 → sudá permutace). Dále permutace je lichá pokud se dá rozložit na sudý počet lichých nezávislých cyklů, nemusíme tedy permutacy rozkládat na transpozice, abychom zjistili sudost/lichost.
Paritu permutace lze také vyjádřit jako (-1)^t, kde t je počet lichých cyklů.
Snad jsem to nenapsal moc nepochopitelně:)

Michal Bednář, 2008/06/12 22:03

*permutacI

Dusan Katona, 2008/06/13 21:00

Ja teda tu (6,6) zrusim, cerpal som z ceskej wikipedie a ako vidno, obcas tam pisu tiez bludy :) (mimo ineho je tam uvedene, ze tato permutacia je licha)
Uplne najjednoduchsie zistenie parity cyklu:
cyklus dlzky n → n-1 transpozíc (n-1 sude → suda, n-1 liche →licha)
Ak mame permutaciu rozlozenu na nezavisle cykly, pomocou tohto 'vzorceku' sa da prist na paritu velmi jednoducho..

Adam Libuša, 2008/06/15 08:30

Hm, podľa mňa princípy exklúzie a inklúzie, ako aj princípy súčtu a súčinu by tam mať boli. Príde mi to tam dôležitejšie ako grupa permutácii.

Adam Libuša, 2008/06/15 08:31

*byť mali :)

Dusan Katona, 2008/06/15 09:50

Riadil som sa podla toho, ze princip inkluze a exkluze v zadani napisany nie je a v zadani pisomnych statnic to je, z coho som vyvodil, ze to z ustnych statnic vylucili :)
Ked tak to tam mozes doplnit…

Adam Libuša, 2008/06/17 15:47

Doplnené.. Dúfam, že je to zrozumiteľné, príklady som si vymyslel, takže ak tam bude chyba, tak to please opravte. Ešte otázka, ako nahrám obrázok na server? Ten jeden čo tam mám sa mi ťahá z homu na aise.

Petr Tvaruzek, 2008/06/17 21:37

mam takovy pocit, ze je chyba v tom odstavci Skladani permutaci. tak jak jsou permutace f1 a f2 definovany, tak by myslim neslo provest f1 PO f2, ale pouze naopak.. nejprve f1 a pak f2, tedy f2 o f1..

Dusan Katona, 2008/06/18 11:34

mas pravdu, opravim to

Kouzelník, 2009/01/30 21:32

Proč v otázce, která zní Elementární kombinatorika, jsou rozebírány vlastnosti a skládání permutací? Kdyť skládání zobrazení (permutací) nijak nesouvisí s kombinatorikou.

Michal Trunečka, 2009/06/11 10:50

Také jsem na to teď narazil. Skládání permutací patří do algebry a ne do kombinatoriky. Já bych to uplně vyhodil a přidal třeba variace, permutace a kombinace s opakováním a podobné záležitosti.

Michal Trunečka, 2009/06/11 10:53

Aha, ok, už to tam je, přehlédnul jsem to, omouvám se.

Karel Hájek, 2009/06/07 01:00

opravil jsem všeobecný vzorec inkluze a exkluze, koeficient posledního členu je (-1)^(n-1), ne (-1)^n. na sk wiki je to špatně.

KosíŘ, 2009/06/07 22:08

To mi chcete říct, že si mám u státnic vymýšlet vlastní příklady (viz poznámku u příkladu na pravidlo součinu)?
Může mi to prosím někdo potvrdit/vyvrátit? (Přijde mi totiž dost ujetý..)

Karel Hájek, 2009/06/09 13:31

pokud neumíš vymyslet příklad, tak tomu imho dost dobře nerozumíš

Lenka, 2009/06/16 20:18

Pridala som príklady na variácie s opakovaním, kombinácie s opakovaním a bez, hádam je to ok :D

Jiří Kůs, 2009/06/18 19:02

„Každá kombinácia k-tej triedy určuje k! variácií, preto môžeme vzorec na výpočet kombinácií odvodiť zo vzorcu na výpočet variácií.“

Podle mě je to tvrzení špatně. Kombinace určuje 1/k! variací a to je imho podstatný rozdíl!

přesněji..
Kombinace = variace, kdy nechceme rozlišovat počet možností, když prvky mají pouze jiné pořadí (k! - z definice permutace)…tedy Ck(n)= Vk(n)/k!

Karel Hájek, 2009/06/30 12:54

Podle mě je to tvrzení dobře.
Každá kombinace k-té třídy určuje k! variací.
po dosazení definicí:
Každý neuspořádaný výběr k prvků určuje k! uspořádaných výběrů k prvků.
Čili na jeden neuspořádaný výběr (kombinaci) připadne k! uspořádaných (variací).
Variací je teda k!-krát víc, což odpovídá vzorci Ck(n)= Vk(n)/k!

You could leave a comment if you were logged in.

home/inf/ap2.txt · Poslední úprava: 2020/04/12 16:56 (upraveno mimo DokuWiki)

Nahoru