Obsah

AP11, IN11 Zásobníkové automaty, Syntaktická analýza
Diskuze

AP11, IN11 Zásobníkové automaty, Syntaktická analýza

Zadání

(definice, převod bezkontextové gramatiky na zásobníkový automat)

(syntaktická analýza shora dolů a zdola nahoru, průběh analýzy daného slova)

Vypracování

Intuice zásobníkového automatu

Zásobníkový automat = PushDown Automaton = PDA

Na vstupní pásce je napsáno slovo (nad jistou vstupní abecedou) – lze z ní pouze číst, čtecí hlava se pohybuje pouze vpravo. Automat může na vrchol zásobníku ukládat symboly (z jisté abecedy) a ty následně číst – čte vždy jen vrchol zásobníku, přečtený symbol je odstraněn = systém LIFO (Last In First Out).

Formální definice

Definice 3.36. - PDA ¹⁾

Nedeterministický zásobníkový automat (PushDown Automaton, PDA) je sedmice $M = (Q, \Sigma, \Gamma, \delta, q_{0}, Z_{0}, F)$ , kde
• Q je konečná množina, jejíž prvky nazýváme stavy,
• $\Sigma$ je konečná množina, tzv. vstupní abeceda,
• $\Gamma$ je konečná množina, tzv. zásobníková abeceda,
• $\delta : (Q \times (\Sigma \cup{{\varepsilon}})\times \Gamma) \rightarrow P_{Fin}(Q \times \Gamma^{*})$ , tzv. (parciální) přechodová funkce (zápis $P_{Fin}(Q \times \Gamma^{*})$ značí množinu všech konečných podmnožin množiny $Q\times \Gamma^{*}$ – dvojice stav a řetězec symbolů zásobníkové abecedy),
• $q_{0} \in Q$ je počáteční stav,
• $Z_{0} \in \Gamma$ je počáteční symbol v zásobníku,
• $F \subseteq Q$ je množina koncových stavů.

$\delta(q_{0}, a, Z_{0}) = \{(q_{0}, AZ_{0})\}; Z_{0}$ … dno zásobníku, A … vrchol zásobníku, přidal se v tomto kroku
$\delta(q_{0}, c, A) = \{(q_{1}, A)\}$ … obsah zásobníku se nezměnil, pouze se přešlo do stavu q₁ $\delta(q_{1}, b, A) = \{(q_{1}, \varepsilon)\}$ … stav se nezměnil, ze zásobníku se přečetlo A – bylo odebráno
vrchol zásobníku běžného PDA se píše vlevo

Výpočet zásobníkového automatu

Definice 3.37. Konfigurace, krok výpočtu ²⁾

Nechť $M = (Q, \Sigma, \Gamma, \delta, q_{0}, Z_{0}, F)$ je PDA.
Konfigurací nazveme libovolný prvek $(p, w, \alpha) \in Q \times \Sigma^{*} \times \Gamma^{*}$ .
Na množině všech konfigurací automatu M definujeme binární relaci krok výpočtu $|\frac{\ \ \ }{\ M \ }$ takto:
$(p, aw, Z \alpha) |\frac{\ \ \ }{\ M \ }(q, w, \gamma \alpha) \Leftrightarrow^{def} \exists(q, \gamma) \in \delta (p, a, Z)$ pro $a \in \Sigma \cup \lbrace \varepsilon \rbrace$

Reflexivní a tranzitivní uzávěr relace $|\frac{\ \ \ }{\ M \ }$ značíme $|\frac{\ * \ }{\ M \ }$ .
Je-li M zřejmý z kontextu, píšeme pouze $|\frac{\ \ \ }{\ \ \ }$ resp. $|\frac{\ * \ }{\ \ \ }$ .

Akceptující výpočet PDA

Definice 3.37. (pokračování) - akceptování ³⁾

Jazyk akceptovaný PDA M koncovým stavem definujeme jako
$L(M) = \lbrace w \in \Sigma^{*} | (q_{0}, w, Z_{0}) |\frac{\ * \ }{\ \ \ } (q_{f}, \varepsilon, \alpha)$ , kde $q_{f} \in F, \alpha \in \Gamma^{*} \rbrace$

a jazyk akceptovaný PDA M prázdným zásobníkem definujeme
$L_{e}(M) = \lbrace w \in \Sigma^{*} | (q_{0}, w, Z_{0}) |\frac{\ * \ }{\ \ \ } (q, \varepsilon, \varepsilon)$ , kde $q \in Q \rbrace$ .

Takto definovaný PDA je nedeterministický – akceptuje slovo, jestliže existuje alespoň jeden výpočet, který vede z počáteční konfigurace do akceptující. V případě možnosti automat „hádá správně“.

Grafická reprezentace konfigurací

Zpravidla nekonečné
Vnitřní konfigurace (= částečná konfigurace) = aktuální stav a celý obsah zásobníku (vrchol se píše vlevo)

Příklad: PDA $A = (\{q, r\}, \{a, b, c\}, \{Z, A\}, \delta, q, Z, \{r\})$ - akceptuje koncovým stavem
PDA $A'= (\{q, r\}, \{a, b, c\}, \{Z, A\}, \delta, q, Z, \emptyset)$ - akceptuje prázdným zásobníkem

Přechodovou funkci mají oba automaty stejnou:
$\delta(q, a, Z) = \{(q, AZ)\}$ $\delta(q, a, A) = \{(q, AA)\}$ $\delta(q, c, Z) = \{(r, Z)\}$ $\delta(q, c, A) = \{(r, A)\}$ $\delta(r, b, Z) = \{(r, \epsilon)\}$ $\delta(r, b, A) = \{(r, \epsilon)\}$

Grafické znázornění obou automatů, žlutě vybarvené jsou konfigurace, ve kterých akceptuje automat A, v tlustě orámované konfiguraci akceptuje automat A'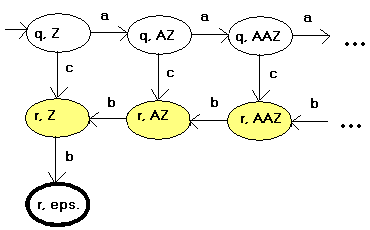

Ekvivalence dvou způsobů akceptování

Pro každý jazyk L platí:

Věta 3.39, ⁴⁾

$L = L(N)$ pro nějaký PDA N $\Leftrightarrow L = L_{e}(M)$ pro nějaký PDA M.

PDA N akceptuje koncovým stavem, PDA M prázdným zásobníkem

koncový stav => prázdná paměť

Intuice: K danému N zkonstruujeme M simulující jeho činnost.
Vejde-li N do koncového stavu, M se nedeterministicky rozhodne
• pokračovat v simulaci automatu N nebo
• přejít do nově přidaného stavu $q_{\varepsilon}$ , v němž vyprázdní zásobník.
Komplikace: Automat N by vyprázdnil zásobník, aniž by došel do koncového stavu – akceptoval by i nežádoucí vstup.
Řešení: Před zahájením simulace bude u M na dně zásovníku nový symbol, který nedovolíme odstranit jinde, než ve stavu $q_{\varepsilon}$ .

prázdná paměť => koncový stav

K danému M zkonstruujeme N simulující jeho činnost.
• N si před simulací přidá na dno zásobníku nový symbol.
• Je-li N schopen číst tento symbol (tj. zásobník automatu M je prázdný), potom N přejde do nově přidaného stavu $q_{f}$ , který je koncovým stavem.

důkaz viz skripta ⁵⁾, konstrukce viz slidy ⁶⁾

Rozšířený zásobníkový automat

Definice 3.44., Rozšířený PDA ⁷⁾

- sedmice $R = (Q, \Sigma, \Gamma, \delta, q_{0}, Z_{0}, F)$ , kde
• všechny symboly až na $\delta$ mají stejný význam jako v definici PDA,
• $\delta$ je zobrazením
z konečné podmnožiny množiny $Q \times (\Sigma \cup \lbrace \varepsilon \rbrace)\times\Gamma^{*}$ ,
do konečných podmnožin množiny $Q \times \Gamma^{*}$ .

Pojmy konfigurace a akceptovaný jazyk (koncovým stavem, prázdným zásobníkem) zůstávají beze změny. Krok výpočtu $|\frac{\ \ \ }{\ R \ }$ definujeme takto:
$(p, aw, \gamma_{1} \alpha) |\frac{\ \ \ }{\ R \ } (q, w, \gamma_{2} \alpha) \Leftrightarrow^{def} \exists(q, \gamma_{2}) \in \delta (p, a, \gamma_{1})$ pro $a \in \Sigma \cup \lbrace \varepsilon \rbrace$

Ekvivalence rozšířených PDA a PDA

Lemma 3.45. ⁸⁾

Ke každému rozšířenému PDA existuje ekvivalentní (obyčejný) PDA.

(Důkaz: skripta Formální jazyky a automaty I, str. 82)

Zásobníkové automaty a bezkontextové jazyky

Problém syntaktické analýzy pro bezkontextové gramatiky: pro danou bezkontextovou gramatiku G a slovo w rozhodnout, zda $w \in L(G)$ .

Ekvivalence bezkontextových gramatik a zásobníkových automatů

Věta 3.51 ⁹⁾

Ke každému PDA M lze sestrojit CFG G takovou, že $L_{e}(M) = L(G)$ .

Věta 3.47 ¹⁰⁾

Ke každé CFG G lze sestrojit PDA M takový, že $L(G) = L_{e}(M)$ .

Důsledek 3.52 ¹¹⁾

Třída jazyků rozpoznávaných zásobníkovými automaty je právě třída bezkontextových jazyků.

Konstrukce PDA řeší problém syntaktické analýzy. (platí pro dané G a w: $w \in L(G)?$ )
$w \in L(G) \Leftrightarrow$ v G existuje derivační strom s výsledkem w.

Nedeterministická syntaktická analýza shora dolů

Budování derivačního stromu simuluje levé derivace, tj. vždy rozvíjíme nejlevější neterminál.

Důsledek 3.47 ¹²⁾

Ke každé CFG G lze sestrojit PDA M takový, že $L(G) = L_{e}(M)$ .

Důkaz. K dané gramatice G konstruujeme PDA M, který simuluje levé derivace v G (rozvíjíme nejlevější neterminál).

V levé derivaci je v jednom kroku odvození nahrazen (nejlevější) neterminál A pravou stranou $X_{1} ...X_{n}$ nějakého A-pravidla.
V M této situaci odpovídá náhrada A na vrcholu zásobníku řetězem $X_{1} ...X_{n}$ .

$M = (\lbrace q \rbrace, \Sigma,N \cup \Sigma, \delta, q, S, \emptyset)$ , kde $\delta$ je definována:

$\delta(q, \varepsilon, A)$ obsahuje $(q, \alpha)$ právě když $A \rightarrow \alpha \in P$
$\delta(q, a, a) = \lbrace(q, \varepsilon)\rbrace$ pro všechna $a \in \Sigma$

korektnost + důkaz viz skripta ¹³⁾

Nedeterministická syntaktická analýza zdola nahoru

Lemma 3.55 ¹⁴⁾

Nechť G je libovolná CFG, pak lze zkonstruovat rozšířený PDA R takový, že L(G) = L(R).

Důkaz. Vrchol zásobníku píšeme vpravo. Konstruujeme rozšířený PDA R, který simuluje pravou derivaci v G v obráceném pořadí.
PDA R má kroky dvojího typu:

může kdykoli číst do zásobníku vstupní symbol,
(redukce) je-li na vrcholu zásobníku řetěz tvořící pravou stranu nějakého pravidla v G, může ho nahradit odpovídajícím levostranným neterminálem (a ze vstupu nic nečte).

Nechť $G = (N, \Sigma, P, S)$ .
Položme $R = (\lbrace q, r \rbrace, \Sigma, N \cup \Sigma \cup \lbrace \bot \rbrace, \delta, q, \bot, \lbrace r \rbrace )$ , kde $\bot$ je nově přidaný symbol a kde $\delta$ je definována takto:

$\delta(q, a, \varepsilon) = \lbrace(q, a)\rbrace$ pro všechna $a \in \Sigma$ …načítání vstupu na zásobník,
je-li $A \rightarrow \alpha$ , pak $\delta(q, \varepsilon, \alpha)$ obsahuje (q, A) …redukce,
$\delta(q, \varepsilon, \bot S) = \lbrace(r, \varepsilon)\rbrace$ …akceptování.

korektnost viz slajdy ¹⁵⁾

Příklad:

Zadání:
G = ({S, A, B}, {a, b}, P, S)
P =
{S → $\varepsilon$ | abSA
A → AaB | aB | a,
B → aSS | bA | $\varepsilon$ }
Derivační strom pro slovo w = abababaa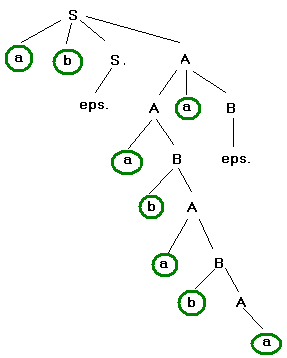
Automat, který provádí syntaktickou analýzu shora dolů: A = ({q}, {a,b}, {S, A, B, a, b}, $\delta$ , q, S, $\emptyset$ )
2 typy přechodových fcí:

levou stranu pravidel z gram. dáváme na zásobník levé strany přechodové fce PDA, pravou stranu pravidel z gram. na zásobník pravé strany

$\delta$ (q, $\varepsilon$ , S) = {(q, $\varepsilon$ ), (q, abSA)}
$\delta$ (q, $\varepsilon$ , A) = {(q, AaB), (q, aB), (q, a)}
$\delta$ (q, $\varepsilon$ , B) = { (q, aSS), (q, bA), (q, $\varepsilon$ )}

„mazací“ přechodové fce

$\delta$ (q, a, a) = {(q, $\varepsilon$ )}
$\delta$ (q, b, b) = {(q, $\varepsilon$ )}

Akceptující výpočet nad slovem abababaa:

(intuice: postupuju podle derivačního stromu, sleduju jeho rozvíjení odshora a čtu ho zleva)
vrchol zásobníku je vlevo $(q, abababaa, S) |\frac{\ \ \ }{\ \ \ } (q, abababaa, abSA) |\frac{\ \ \ }{\ \ \ } (q, bababaa, bSA) |\frac{\ \ \ }{\ \ \ }$
$(q, ababaa, SA) |\frac{\ \ \ }{\ \ \ } (q, ababaa, A) |\frac{\ \ \ }{\ \ \ } (q, ababaa, AaB) |\frac{\ \ \ }{\ \ \ }$
$(q, ababaa, aBaB) |\frac{\ \ \ }{\ \ \ } (q, babaa, BaB) |\frac{\ \ \ }{\ \ \ } (q, babaa, bAaB) |\frac{\ \ \ }{\ \ \ }$
$(q, abaa, AaB) |\frac{\ \ \ }{\ \ \ } (q, abaa, aBaB) |\frac{\ \ \ }{\ \ \ } (q, baa, BaB) |\frac{\ \ \ }{\ \ \ }$
$(q, baa, bAaB) |\frac{\ \ \ }{\ \ \ } (q, aa, AaB) |\frac{\ \ \ }{\ \ \ } (q, aa, aaB) |\frac{\ \ \ }{\ \ \ }$
$(q, a, aB) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, B) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, \varepsilon)$ … celé slovo se přečetlo a zásobník se vyprázdnil $\rightarrow$ automat slovo akceptuje

Automat pro syntaktickou analýzu zdola nahoru: $A_{2} = (\{q, r\}, \{ a,b\} , \{S, A, B, a, b, \bot\}, \delta, q, \bot, \{ r\})$ 3 typy přechodových funkcí:

terminály z gramatiky se předávají na zásobník

$\delta$ (q, a, $\varepsilon$ ) = {(q, a)}
$\delta$ (q, b, $\varepsilon$ ) = {(q, b)}

pravou stranu pravidel z gram. dáváme na zásobník levé strany přechodové fce PDA, levou stranu pravidel z gram. na zásobník pravé strany

$\delta$ (q, $\varepsilon$ , abSA) = {(q, S)}
$\delta$ (q, $\varepsilon$ , $\varepsilon$ ) = {(q, S), (q, B)} ! ! ! Nesmí být rozděleno na: $\delta$ (q, $\varepsilon$ , $\varepsilon$ ) = {(q, S)} a $\delta$ (q, $\varepsilon$ , $\varepsilon$ ) = {(q, B)}, nebyla by to pak funkce.
$\delta$ (q, $\varepsilon$ , AaB) = $\delta$ (q, $\varepsilon$ , aB) = $\delta$ (q, $\varepsilon$ , a) = {(q, A)}
$\delta$ (q, $\varepsilon$ , aSS) = $\delta$ (q, $\varepsilon$ , bA) = {(q, B)}

přechod do koncového stavu

$\delta$ (q, $\varepsilon$ , $\bot$ S) = {(r, $\varepsilon$ )}

Akceptující výpočet nad slovem abababaa:

(Intuice: čtu derivační strom zleva – jako když teče voda (= používám první skupinu pravidel), pokud by voda musela téct do kopce, použiju pravidlo z druhé skupiny)
vrchol zásobníku je vpravo $(q, abababaa, \bot) |\frac{\ \ \ }{\ \ \ } (q, bababaa, \bot a) |\frac{\ \ \ }{\ \ \ } (q, ababaa, \bot ab) |\frac{\ \ \ }{\ \ \ }$
$(q, ababaa, \bot abS) |\frac{\ \ \ }{\ \ \ } (q, babaa, \bot abSa) |\frac{\ \ \ }{\ \ \ } (q, abaa, \bot abSab) |\frac{\ \ \ }{\ \ \ }$
$(q, baa, \bot abSaba) |\frac{\ \ \ }{\ \ \ } (q, aa, \bot abSabab) |\frac{\ \ \ }{\ \ \ } (q, a, \bot abSababa) |\frac{\ \ \ }{\ \ \ }$
$(q, a, \bot abSababA) |\frac{\ \ \ }{\ \ \ } (q, a, \bot abSabaB) |\frac{\ \ \ }{\ \ \ } (q, a, \bot abSabA) |\frac{\ \ \ }{\ \ \ }$
$(q, a, \bot abSaB) |\frac{\ \ \ }{\ \ \ } (q, a, \bot abSA) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, \bot abSAa) |\frac{\ \ \ }{\ \ \ }$
$(q, \varepsilon, \bot abSAaB) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, \bot abSA) |\frac{\ \ \ }{\ \ \ } (q, \varepsilon, \bot S) |\frac{\ \ \ }{\ \ \ } (r, \varepsilon, \varepsilon)$ … automat přečetl celé slovo a přešel do koncového stavu r, slovo akceptuje.

U nedeterministické analýzy automat slovo neakceptuje, pokud žádný z možných výpočtů není akceptující.

Efektivnost syntaktické analýzy

Nederministický PDA ⇒ nedeterministický algoritmus ⇒ exponenciální deterministický algoritmus

Řešení: • deterministický algoritmus složitosti $O(n^{3})$ , kde n = |w| (algoritmus Cocke – Kasami – Younger)
• deterministické zásobníkové automaty a deterministické bezkontextové jazyky
• lineární algoritmy pro speciální třídy deterministických bezkontextových jazyků

C - Y - K algoritmus (Cocke - Younger - Kasami)

Problém: Lze v dané gramatice v CNF vygenerovat dané slovo w?
Řešení: Pro každé podslovo u slova w spočítáme množinu $T_{u}$ všech neterminálů, z kterých lze odvodit u.
* u = a
* u = ab
* u = abc
$T_{i, j} = \{ X| X \Rightarrow^{*} w_{i}w_{i+1}...w_{i+j}w_{i+j-1}\}$

Kubická složitost vzhledem k délce vstupního slova (velikost tabulky: $\frac{n^{2}}{2}$ , na vyplnění políčka je zapotřebí až n kroků.
Pracuje pouze s gramatikou v CNF (Chomského normální formě)

Algoritmus:

Algoritmus C - Y - K

Vstup: gramatika $G = (N, \Sigma, P, S)$ v CNF, slovo $w = w_{1}...w_{n}$ Poznámka: $T_{i,j} = {X | X \rightarrow^{*} w_{i}...w_{i+j-1}}$ for i:=1 to n do
$T_{i,1} := \bot$ for každé pravidlo $A \rightarrow a \in P$ do
if $a = w_{i}$ then $T_{i,1} := T_{i,1} \cup \lbrace A \rbrace$ fi
od od
for j:=2 to n do
for i:=1 to n-j+1 do
$T_{i,j}:= \bot$ for k:=1 to j-1 do
for každé pravidlo $A \rightarrow BC \in P$ do
if $B \in T_{i, k} \wedge C \in T_{i+k, j-k}$ then $T_{i, j}:= T_{i, j} \cup$ {A} fi

od od od od

Příklad

Je dána bezkontextová gramatika G = ({S,A,B,C}, {a, b, c, d}, P, S) v CNF, kde
P = { S → AA | BC | a | b,
A → BA | BB | a | c,
B → AB | CA | b,
C → BC | CC | SC | d }
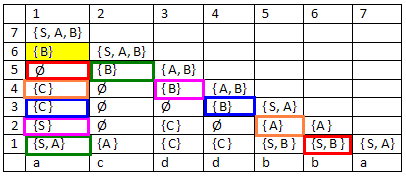
Syntaktická analýza slova $acddbba$ pomocí C-K-Y algoritmu:

Vidíme, že $S \in T_{1,7} = {S,B,A}$ , tedy $acddbba \in L(G)$ .

Intuitivní návod na vyplňování tabulky:

na nultý řádek napíšeme slovo, které chceme testovat (co sloupeček, to 1 terminál)
obsah každého políčka v 1. řádku tvoří množina neterminálů, ze kterých se vygenerují terminály v příslušném sloupečku nultého řádku
další řádky se vyplňují stylem, který je naznačený u žlutého políčka: do množiny v políčku se zapíší všechny neterminály, které generují všechny dvojice neterminálů z příslušných dvojic políček - každá používaná dvojice políček je orámovaná stejnou barvou.

Pro žluté políčko vezmeme jednu z dvojic políček - např. tu orámovanou zeleně. Vzniklé dvojice neterminálů jsou SB a AB. SB není generována žádným neterminálem, tedy do žlutého políčka nepřipisuju nic. AB je generovaná B, proto B zapíšu do žlutého políčka. Stejně postupuju i u ostatních dvojic políček.

Možnost, jak vybírat správné dvojice políček: začínám políčkem, které je nejníž v příslušném sloupečku a políčkem, který je nejblíž v úhlopříčce směrem doprava (pro žluté políčko to jsou zelené rámečky) a dál postupuju (podle krásně jednoduchého návodu Vaška Brožka:), tak že lezu nahoru po žebříku (ve sloupečku) a sestupuju po schodech (v úhlopříčce).

Předměty

IB102 Automaty a gramatiky IB005 Formální jazyky a automaty I

Literatura

Skripta Formální jazyky a automaty I
Slajdy k přednáškám IB102 na stránkách Jana Strejčka

Vypracoval

Didl - Dita Dlabolová
Stav: 100%, z mé strany hotovo a zkontrolováno.

Je potřeba ještě zapracovat poznámky od Jitky Pospíšilové.

¹⁾

skripta Automaty a formální jazyky I, str. 77

²⁾ , ³⁾ , ⁴⁾

skripta Automaty a formální jazyky I, str. 78

⁵⁾

skripta Automaty a formální jazyky I, str. 78

⁶⁾

Web IB102 - slajdy10, str. 5 a 8

⁷⁾ , ⁸⁾

skripta Formální jazyky a automaty I, str. 82

⁹⁾

skripta Formální jazyky a automaty I, str. 86

¹⁰⁾ , ¹²⁾

skripta Formální jazyky a automaty I, str. 83

¹¹⁾

skripta Formální jazyky a automaty I, str. 89

¹³⁾

str. 84 skripta Formální jazyky a automaty I, slajdy11 - str. 12

¹⁴⁾

skripta Formální jazyky a automaty I, str. 90

¹⁵⁾

slajdy11, str. 17

Diskuze

Jan Palas, 2008/05/27 20:55

Ahoj, problémy s hvězdičkou a symbolem pro krok výpočtu se dají vyřešit :) Jen musíš matematické vzorce uzavírat do tagů <math></math> a ne <m></m> jak to máš ty. Uvnitř tagů <math> ale musíš používat normální LaTeXovou syntax - koukal jsem, že tam máš poněkud odlišnou. Takže například symbol $\Gamma$ nebude prosté Gamma ale \Gamma atd. Takže $\Gamma^{\ast}$ napíšeš jako <math>\Gamma^{\ast}</math> a symbol pro krok výpočtu jako <math>\vdash</math>. Aspoň mě to fungovalo když jsem si to zkoušel na zdejším playgroundu. Myslím, že bude lepší, když si to upravíš sama - chvíli jsem to zkoušel, ale byla to pro mě dost chaotická práce, asi se v tom sama lépe vyznáš ;)

Dita Dlabolová, 2008/05/28 20:39

Díky moc:) já jsem to dělala podle toho, co je tady na playgroundu, protože latex je pro mě španělská vesnice :))
Každopádně jsem to teď zkoušela opravit a chová se to nějak divně… prostě se to odmítá zobrazovat, ale jen někde… bohužel se mi nepodařilo vysledovat proč… na playgroundu to funguje všechno :)

Jitka Pospíšilová, 2008/05/29 14:06

Ahoj, co jsem si zkousela ja, tak nejde kombinovat oba pluginy <m> a <math>, musis si vzbrat jen jeden…

Tomas Drexler, 2008/06/03 16:14

Ahoj, prijde mi, ze v te syntakticke analyze zdola nahoru mas v teorii zasobnik PDA vpravo a v prikladu zase vlevo.

Dita Dlabolová, 2008/06/03 21:29

Já to mam akorát zmateně napsaný, protože nejdřív v teorii říkám, že vrchol je vpravo a pak, že dno je vlevo, takže je to obojí stejně, akorát prostě blbě řečený :) Všechno to předělám, aby to bylo stejně… Díky za připomínku ;-)

→ Jitka: díky, to mi nedošlo ;-) Zatím to nechám, jak to je, snad časem.. :)

Dusan Katona, 2008/06/10 20:55

Ahoj,
chcem sa len opytat, myslite, ze je nutne poznat algoritmus C-Y-K? My na teoretickej informatike sme sa ho vobec neucili, nestacilo by len vediet analyzovat dane slovo pomocou zasobnikoveho automatu? (podla mna ano)

Marek Babák, 2008/06/17 19:25

Já se jej asi taky učit nebudu, taky jsem ho na teoretické zahlédl jen ve skriptech. Podle mě stačí (aspoň pro teoretický) umět syntaktickou analýzu odzvrchu dolu a odspodu nahoru :)

Tomáš Gazárek, 2008/06/11 16:26

Ahoj,
nevíte někdo jaký je rozdíl mezi oborem hodnot u přechodové funkce a u rozšířené přechodové funkce?
U přechodové funkce se píše, že delta je zobrazení z definičního oboru do $P_{Fin}(Q × Gamma^*)$ .
U rozšířené funkce se píše, že je to zobrazení z definičního oboru do konečných podmnožin množiny .
Jsou ty obory hodnot stejné nebo se liší? Nějak to v tom nevidím. Dík

Michal Smejkal, 2008/06/12 07:36

Cau,
rodil mezi tim neni zadny.
„P fin“ se slovne vyjadruje jako „mnozina vsech konecnych podmnozin“
Takze u prvniho pripadu to mas vyjadreno SYMBOLEM a u druheho pripadu to je SLOVNE.

Dita Dlabolová, 2008/06/12 17:25

→ Dušan: v zadání se na to neptají, takže to asi nebude požadovaný. Imho určitě neuškodí, když zmíníš, že nějaký deterministický algoritmus existuje. Ale nejspíš stejně čas na jeho předvádění nebo popis nezbyde .-)

→ Tomáš: je to to samé. Opsala jsem to, jak je to ve skriptech, žádné záměrné matení z mé strany ;-)

Jitka Pospíšilová, 2008/06/12 23:59

uff… tak jsem se pustila do prepisu tech matematickych symbolu do druheho pluginu… nekolikrat jsem kontrolovala s puvodni verzi, takze by se tam (snad) nemela vloudit zadna chybicka. Taky jsem si dovolila uz oddelat tu uvodni poznamku k wiki syntaxi.

Dita Dlabolová, 2008/06/13 23:19

→ Klobouk dolů, že ses do toho pustila :) Jasně, ta poznámka by tam teď byla už zbytečná…

Roman Plášil, 2008/06/14 12:38

Nahrál jsem obrázky sem na server, aby to bylo nezávislé na vnějším světě.

Erik Zitterbart, 2008/06/20 13:59

Nemela by byt soucasti odpovedi na otazku i Deterministicka analyza shorad dolu?

Marek Babák, 2008/06/20 15:02

Vzdyt tam je…

Erik Zitterbart, 2008/06/21 12:51

Vyjadril jsem se trochu nepresne. Jiste ze algoritmus C-Y-K je deterministicky. Ve slajdech k predmetu Automaty a gramatiky je zminea Deterministicka syntakticka analyza shora dolu. Obsahuje pojmy jako FIRST, FOLLOW. Ta zde neni uvedena. Proc?

Erik Zitterbart, 2008/06/21 13:33

Tak jsem se tomu snažil podívat trochu na zub. Možná to někoho bude zajímat:
PDA je deterministický (DPDA) jestliže platí:

pro všechna q ∈ Q a Z ∈ Γ platí: kdykoliv δ(q,ε,Z) ≠ ∅, pak δ(q,a,Z) = ∅ pro všechna a ∈ ∑.
pro žádné q ∈ Q, Z ∈ Γ a a ∈ ∑ ∪ {ε} neobsahuje δ(q,a,Z) více než jeden prvek.

Řekneme, že jazyk L je nedeterministický bezkont. jazyk (DFCL), právě když existuje DPDA M, takový, že L = L(M).

!! Existují bezkontextové jazyky, které nejsou deterministickými bezkontextovými jazyky.

Řekl bych, že tedy není nutné znát Deterministickou syn. analýzu shora dolů. V zadání se totiž zmiňují bezkontextové jazyky a NE nedeterministické bezkontextové jazyky.

Adam Jurčík, 2008/06/20 18:48

Ja mam jen takovou malou poznamku, pokud ji uznate za nepodstatnou tak ji kdyztak smazte.

Grafické znázornění obou automatů, žlutě vybarvené stavy jsou akceptující stavy automatu A, tlustě orámovaný stav je akceptující stav automatu A'

Tady bych spise napsal konfigurace misto slova stavy, jen kvuli zdrurazneni, ze nejde o zobrazeni stavu ze stavove jednotky a kvuli tomu, ze akceptujici stav u PDA akceptujiciho prazdnym zasobnikem nedava smysl.

Adam Jurčík, 2008/06/20 20:49

Ja mam jen takovou malou poznamku, pokud ji uznate za nepodstatnou tak ji kdyztak smazte.

Grafické znázornění obou automatů, žlutě vybarvené stavy jsou akceptující stavy automatu A, tlustě orámovaný stav je akceptující stav automatu A'

Tady bych spise napsal konfigurace misto slova stavy, jen kvuli zdrurazneni, ze nejde o zobrazeni stavu ze stavove jednotky a kvuli tomu, ze akceptujici stav u PDA akceptujiciho prazdnym zasobnikem nedava smysl.

Dita Dlabolová, 2008/06/22 18:26

→Adam: Jasně, máš pravdu, jsou to konfigurace, né stavy, upsala jsem se…
Díky za připomínku…

→ Erik: Snad by tam být deterministická analýza neměla, v první verzi otázek byla (otázka zněla: „Syntaktická analýza (syntaktická analýza shora dolů a zdola nahoru, syntaktická analýza deterministických bezkontextových jazyků metodou shora dolů, konstrukce LL(1) analyzátoru, průběh analýzy daného slova)“), ale na informační schůzce jsme si stěžovali, že se letos se na IB102 neprobírala, proto byla tahle otázka sloučená s otázkou na zás. automaty, kde už se o deterministický analýze nemluví, takže pevně věřím, že ji nikdo po nás chtít nebude (den před začátkem státnic mi nic jinýho než víra nezbývá :-D )

patrik, 2011/01/18 00:20

detail na časť „Grafická reprezentace konfigurací“: ten hrubo orámovaný stav „r,eps.“ v ňom by mali akceptovať oba automaty A' aj A, alebo sa mýlim? ak neakceptuje poprosím aj vysvetlenie

Matej Červeňák, 2011/01/20 02:59

Ja som sa tiez pri tom pozastavil a myslim, ze je to tak, ako pises ty. Nevidim dovod preco nie, kedze su pravidla rovnake pre obe „varianty“ PDA. Ale ze by si taku chybicku za 3 roky nikto nevsimol :/ ???

You could leave a comment if you were logged in.

home/inf/ap11.txt · Poslední úprava: 2020/04/12 16:56 (upraveno mimo DokuWiki)

Nahoru