Obsah

AP13 Prolog
- Zadání
Vypracování
Literatura
Diskuze

AP13 Prolog

Zadání

(SLD-rezoluce, SLD-stromy, výpočetní mechanismus Prologu, základy programování v Prologu)

Vypracování

Rezoluce

Rezoluce –- dokazuje se nesplnitelnost formulí, jsou v KNF, v kořenu je □ a nebo dokazovaná formule C, v listech jsou jednotlivé klauzule S, ve vnitřních listech resolventy

Lineární rezoluce –- jde o posloupnost dvojic $<C_{0}, B_{0}>$ , … , $<C_{n}, B_{n}>$ takovou, že $C = C_{n+1}$ a

$C_{0}$ a všechny $B_{i}$ jsou z S anebo nějaké $C_{j}$ , kde $j<i$
každé $C_{i+1}$ , $i \leq n$ je rezolventou $C_{i}$ a $B_{i}$ (vstupní klauzule S, boční $B_{i}$ a střední $C_{i}$ )

je korektní a úplná

Lineární vstupní rezoluce (LI) množiny $S=P \cup \{ G\}$ je lineární vyvrácení S, které začíná klauzulí G, a bočními klauzulemi jsou jen klauzule z P.

je úplná jen pro Hornovy klauzule

Hornovy klauzule (jsou v Prologu) = klauzule s nejvýše jedním pozitivním literálem (dají se reprezentovat jako implikace)

Typy:

programové –- fakta (bez negativního literálu. p.), pravidla (s aspoň 1 negativním literálem p:-q.)
cíle –- bez pozitivního literálu ?-p. (t.j. ekvivalent {neg p})

LD rezoluce –- už máme uspořádané klauzule a při rezoluci vkládáme dovnitř. LD rezoluční vyvrácení $P \cup \{ G\}$ je postupnost $<G_{0}, C_{0}>$ , … , $<G_{n}, C_{n}>$ uspořádaných klauzulí taková, že $G_{0}=G, G_{n+1}=$ □, $C_{i} \in T$ a každé $G_{i}$ , $1\leq i\leq n$ je rezolventou uspořádaných klauzulí $G_{i-1}$ a $C_{i-1}$

SLD-rezoluce

SLD rezoluce -– lineární vstupní rezoluce se selekčním pravidlem (selekční pravidlo = libovolná funkce, která vybere literál z každé uspořádané cílové klauzule)

úplnost SLD-rezoluce pro Prolog, t.j. pro Hornovy klauzule (umí to určitě vyvrátit, když je to možné)
pomocí selekčního pravidla algoritmizujeme výběr literálu z cílové klauzule, na které se bude rezolvovat
SLD-rezoluce je korektní a úplná pro Hornovy klauzule
budeme používat nejlevější literál

Význam SLD rezoluce

: máme množinu klauzulí P a cílovou klauzuli $G=[\neg A_{1}(\vec{x}) \cdots \neg A_{n}(\vec{x})]$

dokazujeme nesplnitelnost $P \cup \lbrace G \rbrace$ , tj. $P \wedge \forall \vec{x}(\neg A_{1}(\vec{x}) \cup \cdots \cup \neg A_{n}(\vec{x}))$
uvedená nesplnitelnost je ekvivalentní $P \vdash \neg G$ , tj. $P \vdash \exists \vec{x}(A_{1}(\vec{x}) \wedge \cdots \wedge A_{n}(\vec{x}))$
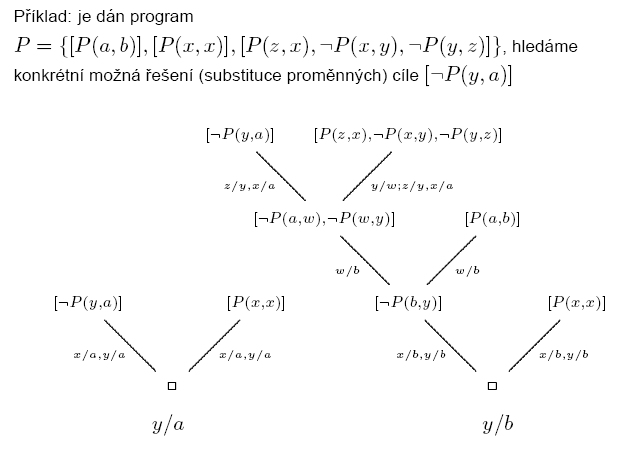
zadáním cíle G tedy chceme zjistit, zda existují nějaké objekty, které na základě P splňují formuli $A_{1}(\vec{x})\wedge \cdots \wedge A_{n}(\vec{x})$
aplikujeme-li kompozici všech mgu postupně použitých při SLD-odvození na jednotlivé proměnné vektoru $\vec{x}$ , získáme konkrétní případy zmíněných objektů splňujících danou formuli

Příklad(1)

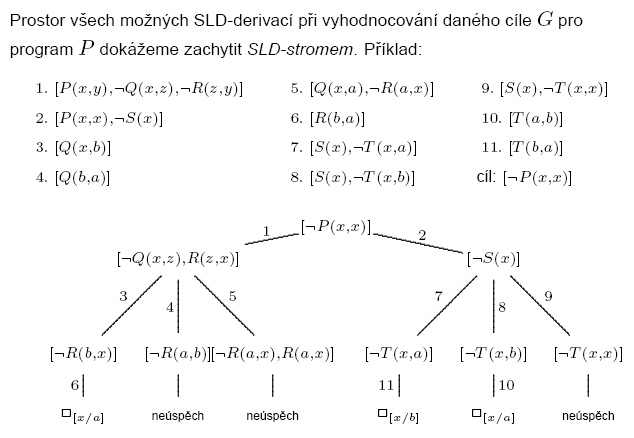
SLD-stromy

SLD strom pro program P a cíl G: v kořeni je G. Když je libovolný uzel označený G‘, tak jeho bezprostřední následníci jsou označení výsledkem rezoluce nejlevějšího literálu G‘ se všemi použitelnými klauzulemi z P.

takto vznikne hodně cest, i ty neúspěšné,
vždy v každém uzlu jsou všechny literály negované

Příklad(2)

EDIT: Tento příklad obsahuje chybu - doporučuji se podívat na interaktivní přednášku pana Popelínského:¹⁾ Chyba je hned na 1. řádku.
Ten má vypadat takto: $1. [P(x,y),\neg Q(x,z), R(z,y)]$

Prolog

Prolog je logický programovací jazyk. Patří mezi tzv. deklarativní programovací jazyky, ve kterých programátor popisuje pouze cíl výpočtu, přičemž přesný postup, jakým se k výsledku program dostane, je ponechán na libovůli systému. Prolog se snaží o pokud možno abstraktní vyjádření faktů a logických vztahů mezi nimi s potlačením imperativní složky. Prolog je využíván především v oboru umělé inteligence a v počítačové lingvistice (obzvláště zpracování přirozeného jazyka, pro nějž byl původně navržen).

Výpočetní mechanismus Prologu

úspěšné cesty v SLD-stromě jsou ty, které končí □, ostatní jsou neúspěšné.

Vyhodnocovací mechanizmus Prologu prochází SLD-strom do hloubky zleva doprava a hledá (první) úspěšnou cestu (backtracking) – případně projde celý strom a vyhlásí, že to není možné.

- zadání středníku (;) po úspěšném vyhodnocení čísla vynutíme backtracking a hledání alternativního důkazu
- odpověď „no“ systému znamená, že daný cíl není logickým důsledkem programu (případně že nemá alternativní důkaz) prologovská strategie prohledávání stavového prostoru (do hloubky) může vést k zacyklení (i v případě, že existují úspěšné větve)

Příklad programu, který vede k zacyklení, i když existují úspěšné větve: q:- r. r:- q. q. ?- q.

Základy programování v Prologu

Logické programování:

logický program = libovolná konečná množina programových Hornových klauzulí
odvozování (dokazování) cílů založené na SLD-rezoluci
deklarativní (specifikace programu je přímo programem)
teoretický model, zachovává úplnost

Prolog

konkrétní implementace logického programovacího jazyka
ztráta úplnosti (možnost zacyklení)
vhodný na řešení problémů týkajících se objektů a vztahů mezi nimi,
do značné míry využívá rekurzi

Syntax : datové objekty

Základem jsou termy (konstanty, proměnné, složené termy)
1. konstanty
  1. celá čísla (0, -12, …)
  2. desetinná čísla (1.0, 4.5E7, …)
  3. atomy ('ježek', [], ==, …)
2. proměnné (N, VYSLEDEK, …)
3. složené termy:
  1. funktor (jméno, arita)
  2. argumenty (bod(X,Y,Z),tree(Value, tree(LV,LL,LR), tree(RV,RL,RR)))

Syntax: program

množina programových klauzulí
proměnné v lokální klauzuli
pravidla: hlava:- tělo.
1. date(D,M,Y):- day(D), month(M), year(Y).
fakta: pravidla s prázdným tělem
cíle: klauzule bez hlavy, reprezentují dotazy

Poznámky

do značné míry využívá rekurzi
patří mezi deklarativní programovací jazyky

využíván v oboru umělé inteligence a zpracování přirozeného jazyka

založen na predikátové logice prvního řádu, zaměřuje se na Hornovy klauzule
1. seznamy
  1. definovány induktivně
  2. [] - prázdný seznam
základní využívané přístupy jsou unifikace a rekurze

anonymní proměnná _ (podtržítko), její hodnota není podstatná
1. používá se v pravidlech je_dite(X):- dite(X,_).
základ Prologu je databáze klauzulí (fakta a pravidla), nad kterou je možno klást dotazy formou tvrzení, kde Prolog vyhodnocuje jejich pravdivost
1. fakta - nejjednodušší klauzule, vypovídající o vlastnostech a vztazích mezi objekty, př. dívka(monika)
2. pravidla - odvozování nových dat pomocí aplikace hlavička:- tělo.
  1. hlavička - odvozovaný fakt
  2. tělo - podmínky
  3. př. syn(A,B):- rodic(B,A), muz(A).

Literatura

Wikipedia Prolog - http://cs.wikipedia.org/wiki/Prolog_%28programovac%C3%AD_jazyk%29 Slidy předmětu - http://www.fi.muni.cz/usr/popelinsky/lectures/bak_logika/ Vypracování otázek Elena Halicová - http://www.fi.muni.cz/~xhalic1/statnice/vypracovaneIM.doc

¹⁾

https://is.muni.cz/auth/th/173318/fi_b/5726674/5726798/3-24.htm

Diskuze

Tomáš Gazárek, 2008/06/09 18:00

Tuto otázku vypracovala Tereza Dvořáková, já ji sem přepsal. Klidně cokoliv dopište pokud si myslíte, že to sem patří.

Jitka Pospíšilová, 2008/06/16 00:20

mela jsem problem s tiskem teto stranky, tak jsem ji narychlo predelala to pluginu math… kontrolovala jsem to a pevne doufam, ze tam nejsou zadne chybky z toho prepisu.

Jitka Pospíšilová, 2008/06/17 14:03

podle me je v prikladu 2 u SLD stromu chyba… maji totiz byt vsechny literaly v uzlech negovane a ve dvou uzlech nejsou…

Pavel Koudela, 2008/06/20 09:11

Ano v druhem prikladu si taky myslim ze je chyba.
Konkretne ve druhem radku ma byt vysledna formule
[-Q(x,z),-R(z,x)]
a potom se chyba posouva i do tretiho radku.
Je to presne jak pises, nejsou negovane a maji byt.

Pavel Koudela, 2008/06/20 09:14

Akorat ted nevim jak je to s temy neuspechy… tam se nemuze provest substituce?

Jitka Pospíšilová, 2008/06/17 14:13

nezda se mi taky ten priklad u Prologu:

q:=r. r:-q. q. cíl ?- q. - respektive, co v nem znamena to “=“?

nemelo by spis byt:

q:-r.
r:-q.
q.
?- q.

EDIT: uz jsem to nasla ve skriptech.. opravuji na spravne.

Marek Blahuš, 2008/06/23 15:14

Doplním aspoň takto formou diskuze svůj výcuc k jednotlivým druhům rezolucí, který se onehdy snad docela ujal v DF dotyčného předmětu. Narozdíl od toho tady v článku je to založené na tvarech těch rezolučních stromů, což se minimálně mně na první pohled lépe chápe než ty formální definice v textu vypracování otázky:

(požadavky se postupně kumulují - pro každou rezoluci platí i vše uvedené pro ty před ní)
1. Obecná rezoluce - strom, spojuje se „cokoliv s čímkoliv“
2. Lineární rezoluce - všechno je na jedné vìtvi
3. LI rezoluce - první klauzule je cíl z dané množiny (taková, kde jsou všechny literály negativní); boèní (přidávané) klauzule bereme pouze ze vstupní množiny (není možná recyklace dříve vyrezolvovaných)
4. LD rezoluce - klauzule jsou uvnitř uspořádané, takže při rezolvování se dva stejné literály zapíší do výsledku dvakrát
5. SLD rezoluce - literál, na kterém rezolvuju, vybírám z aktuální klauzule podle pravidla (obv. zleva)

Michal Straňák, 2011/01/19 21:24

Ja by som len chcel jemne poopravit hned na zaciatku tu definiciu Linearnej rezolucie:

1. C0 patri do S a zaroven Bi patri do S alebo Bi = Cj, kde j<i (to znaci to, ze mozme pouzit v rezolucii uz v nejakom predoslom kroku vzniknutu rezolventu)

Pavel Grochal, 2011/06/07 02:18

S klidem to uprav, pokud máš jistotu, že je to dobře. Domnívám se, že studenti kteří toto udržovali v roce 2008, už sem nezavítají.

-- --, 2011/01/31 04:38

sjednotte pls nekdo posledni sekci „poznamky“ s odstavci predtim, je tam spousta duplicit…

You could leave a comment if you were logged in.

home/inf/ap13.txt · Poslední úprava: 2020/04/12 16:56 (upraveno mimo DokuWiki)

Nahoru