Obsah

AP3, IN3 Uspořádání
Diskuze

AP3, IN3 Uspořádání

(relace uspořádání, uspořádané množiny a svazy, číselné obory)

Vypracovanie

Relace usporiadania

Usporiadanie a predusporiadanie

Relace $R \subseteq M \times M$ je usporiadanie práve vtedy, keď R je reflexívna, antisymetrická a tranzitívna.
Relace $R \subseteq M \times M$ je predusporiadanie (kvaziusporiadanie, polousporiadanie) práve vtedy, keď R je reflexívna a tranzitívna (a neplatí antisymetrie).

Usporiadané množiny

Usporiadaná množina

(Pred)usporiadaná množina je dvojica $(M,\sqsubseteq)$ , kde M je množina a $\sqsubseteq$ je (pred)usporiadanie na M.
Usporiadaná množina $(M,\sqsubseteq)$ sa nazýva lineárne usporiadaná (reťazec), ak $\forall a, b \in M:\ a \sqsubseteq b\ \vee \ b \sqsubseteq a$ (každé dva prvky sú zrovnateľné).

Príkladom lineárne usporiadaných množín sú N, Z, Q, R vzhľadom k usporiadaniu podľa veľkosti. Príkladom predusporiadanej množiny, ktorá nie je usporiadaná je (Z*,|), kde Z* je množina všetkých nenulových celých čísel a | je relace deliteľnosti (množina (N,|) usporiadaná je) ¹⁾.

Na usporiadaných množinách môžeme definovať ďalšie relace usporiadania:

usporiadanie po bodoch

Nech M je množina a $(A,\leq)$ usporiadaná množina. Nech $F = \{f|f:\ M \rightarrow A\}$ . Definujeme binárnu relaci $\sqsubseteq$ na F predpisom:
$f\ \sqsubseteq \ g \ \Leftrightarrow \ \forall x \in M:\ f(x) \leq g(x)$ Potom $(F,\sqsubseteq)$ je usporiadaná množina a usporiadanie $\sqsubseteq$ sa nazýva „po bodoch“.

usporiadanie po zložkách

Nech $(A,\leq)$ a $(B,\preceq)$ sú usporiadané množiny. Definujeme binárnu relaci $\sqsubseteq$ na $A \times B$ predpisom:
$(a,b)\ \sqsubseteq \ (a',b')\ \Leftrightarrow \ a \leq a'\ \wedge \ b \preceq b'$ Potom $(A \times B,\sqsubseteq)$ je usporiadaná množina a usporiadanie $\sqsubseteq$ sa nazýva „po zložkách“.

usporiadanie lexikografické

Nech $(A,\leq)$ a $(B,\preceq)$ sú usporiadané množiny. Definujeme binárnu relaci $\sqsubseteq$ na $A \times B$ predpisom:
$(a,b)\ \sqsubseteq \ (a',b')\ \Leftrightarrow \ (a \leq a'\ \wedge\ a \neq a')\ \vee \ (a = a'\ \wedge \ b \preceq b')$ Potom $(A \times B,\sqsubseteq)$ je usporiadaná množina a usporiadanie $\sqsubseteq$ sa nazýva „lexikografické“. Ak sú usporiadania $\leq$ a $\preceq$ lineárne, je aj usporiadanie $\sqsubseteq$ lineárne.

Nech $(A,\leq)$ je usporiadaná množina.
Najmenší prvok je prvok $x \in A$ taký, že $\forall y \in A:\ x \leq y$ .
Minimálny prvok je prvok $x \in A$ taký, že $\forall y \in A:\ y \leq x \Rightarrow x \leq y$ (x je minimálny práve vtedy, keď neexistuje žiadny prvok menší ako x).
Najväčší prvok je prvok $x \in A$ taký, že $\forall y \in A:\ y \leq x$ .
Maximálny prvok je prvok $x \in A$ taký, že $\forall y \in A:\ x \leq y \Rightarrow y \leq x$ (x je maximálny práve vtedy, keď neexistuje žiadny prvok väčší ako x).

Najmenší (najväčší) prvok, ak existuje, je jediný a zároveň minimálny (maximálny). Minimálnych (maximálnych) prvkov môže byť viac, potom ale neexistuje najmenší (najväčší) prvek.

Usporiadané množiny môžeme prehľadne zobraziť pomocou tzv. Hasseovských diagramov. Nech sú usporiadané množiny zadané nasledovne ²⁾: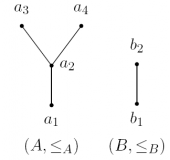
Prvok a₁ je minimálny a najmenší, prvky a₃, a₄ sú maximálne. Prvok b₁ je minimálny a najmenší, prvok b₂ maximálny a najväčší.
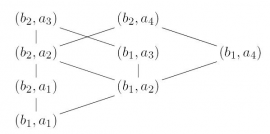
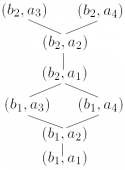
Pomocou Hasseovských diagramov môžeme znázorniť usporiadané množiny $(B \times A, \leq)$ , kde $\leq$ je usporiadanie po zložkách a $(B \times A, \preceq)$ , kde $\preceq$ je lexikografické usporiadanie:

Svazy

Svaz

Svaz je uspořádaná množina $(X,\preceq)$ , ve které existuje supremum i infimum pro libovolnou dvojici prvků. Ve svazu můžeme na supremum a infimum pohlížet jako na binární operace (protože je zaručeno, že jejich hodnoty jsou definovány pro každou dvojici). Supremum prvků x, y zde značíme $x \vee y$ , infimum jako $x \wedge y$ .
Definice svazu ze skript:³⁾.

Nech $(M,\leq)$ je usporiadaná množina.
Prvok $x \in M$ je horná závora množiny $A \subseteq M \Leftrightarrow \forall y\in A:\ y \leq x$ .
Prvok $x \in M$ je suprémum množiny $A \subseteq M$ (supA) $\Leftrightarrow$ x je najmenšia horná závora množiny A (t.j. pre ľubovoľnú hornú závoru y množiny A platí $x \leq y$ ).
Prvok $x \in M$ je dolná závora množiny $A \subseteq M \Leftrightarrow \forall y\in A:\ x \leq y$ .
Prvok $x \in M$ je infimum množiny $A \subseteq M$ (infA) $\Leftrightarrow$ x je najväčšia dolná závora množiny A (t.j. pre ľubovoľnú dolnú závoru y množiny A platí $y \leq x$ ).
Špeciálne prípady:⁴⁾.
Přehledné vysvětlení i s příklady:⁵⁾.
$sup\emptyset$ je najmenší prvok usporiadanej množiny M a $inf\emptyset$ je najväčší prvok M (ak existujú).
V usporiadanej množine $(P(M),\subseteq)$ , kde P(M) je potenčná množina množiny M a X je neprázdna podmnožina P(M) platí:
$supX = \bigcup X$ $infX = \bigcap X$

Veta 1 (Faktická správnost věty 1 je zpochybněna, viz diskusi)

Nech A je usporiadaná množina, potom nasledujúce výroky sú ekvivalentné.

ľuboboľná podmnožina množiny A má infimum
ľuboboľná podmnožina množiny A má suprémum

Dôkaz predchádzajúcej vety môžete nájsť v skriptách ⁶⁾.

Svaz a úplný svaz

Usporiadaná množina A sa nazýva svaz, ak jej ľubovoľná dvojprvková podmnožina má suprémum a infimum.
Nechť (A,∧,∨) je svaz a B je neprázdná podmnožina A. Pak B se nazývá podsvazem svazu A, platí-li, že B je uzavřená vzhledem ke svazovým operacím „∧“ a „∨“, tedy pro všechny a,b z B: a ∧ b náleží B, a ∨ b náleží B.
Usporiadaná množina A sa nazýva úplný svaz, ak jej ľubovoľná podmnožina má suprémum a infimum.

Z predchádzajúcich definícií vyplývajú nasledovné dôsledky:

Ak je $(A,\leq)$ svaz, potom tiež každá neprázdna konečná podmnožina v A má suprémum a infimum. Ak A je konečná (a neprázdna), pojmy svaz a úplný svaz splývajú.
Každý úplný svaz je tiež svaz.
Každý úplný svaz $(A,\leq)$ má najmenší a najväčší prvok, ktorým je $infA$ a $supA$ .

Príklady svazov a úplných svazov:

Každá lineárne usporiadaná množina je svaz, teda aj $(N,\leq)$ , $(Z,\leq)$ , $(Q,\leq)$ , $(R,\leq)$ sú svazy (žiaden z nich nie je úplný svaz (neexistuje supN, supZ), pokud se na uspořádání na daných množinách díváme tak, jak je obvyklé, ovšem tyto množiny lze přeuspořádat tak, aby již byly úplným svazem).
Usporiadaná množina $(N,|)$ je svaz – každá dvojprvková množina $\{a,b\}$ má suprémum (najmenší spoločný násobok a,b) a infimum (najväčší spoločný deliteľ a,b).

Uspořádaná množina $(N_{0},|)$ je úplný svaz. (Záleží tedy i na tom, jak si zadefinujeme relaci |. Například nechť $a,b \in N_{0}$ , $a | b \Leftrightarrow \exists x \in Z^{*}.\ a \cdot x = b\$ .)

Usporiadaná množina $(P(A),\subseteq)$ je úplný svaz, nájdenie supréma a infima ľubovoľnej podmnožiny je popísané vyššie.

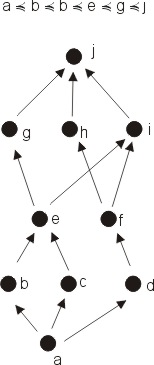
Krásně nakreslený příklad svazu + suprema a infima pro jeho podmnožiny 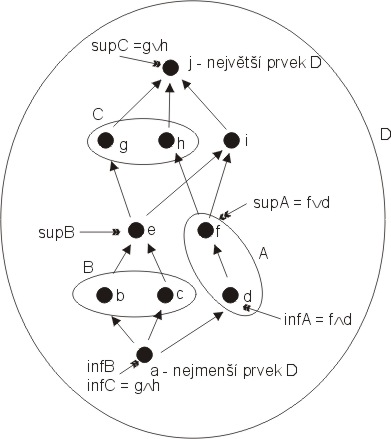zdroj⁷⁾

Číselné obory

Prirodzené čísla

Medzi prirodzené čísla N patria čísla 1, 2, 3, 4, 5,…, do N₀ patrí aj 0. Prirodzené čísla konštruujeme pomocou množín:
$0 = \emptyset$ $1 = \{\emptyset\}$ $2 = \{\emptyset, \{\emptyset\} \}$ $3 = \{ \emptyset, \{\emptyset\}, \{\emptyset, \{\emptyset\}\}\}$ … Vždy platí, že číslo n vyjadríme ako $n = \{0, 1,..., n-1\}$ .

Celé čísla

Celé čísla $Z = \{...,-3,-2,-1,0,1,2,3,...\}$ konštruujeme nasledovným spôsobom:
Definujeme na množine $N_{\small 0}\ \times \ N_{\small 0}$ relaci $\sim$ vzťahom:
$(a,b)\ \sim \ (c,d) \Leftrightarrow a + d = c + b$ Jedná sa o relaci ekvivalence, ak položíme $Z = N_{\small 0}\ \times \ N_{\small 0} / \sim$ , dostaneme rozklad množiny. Triedu ekvivalence $\sim$ určenú prvkom $(a,b)$ označíme $\overline{(a,b)}$ (reprezentuje rozdiel a-b). Definujeme operácie:

$\overline{(a,b)} + \overline{(c,d)} = \overline{(a+c,b+d)}$

$\overline{(a,b)} \cdot \overline{(c,d)} = \overline{(ac+bd,ad+bc)}$

$- \overline{(a,b)} = \overline{(b,a)}$

(tip: operácie sa ľahko pamätajú, ak si pod $\overline{(a,b)}$ predstavíte $a-b$ )
Uvedené definície nezávisia na voľbe reprezentantov ⁸⁾. Prirodzenému číslu n odpovedá celé číslo $\overline{(n,0)}$

Racionálne čísla

Na množine $Z\ \times \ Z^{*}$ ( $Z^{*}$ značí množinu nenulových celých čísel) definujeme relaci $\sim$ vzťahom:
$(a,b)\ \sim \ (c,d) \Leftrightarrow ad = cb$ Jedná sa o relaci ekvivalence, ak položíme $Q = (Z\ \times \ Z^{*}) / \sim$ , dostaneme rozklad množiny. Triedu ekvivalence $\sim$ určenú prvkom $(a,b)$ označíme $\overline{(a,b)}$ (reprezentuje zlomok $\frac{a}{b}$ ). Definujeme operácie:

$\overline{(a,b)} + \overline{(c,d)} = \overline{(ad+bc,bd)}$

$\overline{(a,b)} \cdot \overline{(c,d)} = \overline{(ac,bd)}$

(tip: operácie sa ľahko pamätajú, ak si pod $\overline{(a,b)}$ predstavíte $\frac{a}{b}$ )
Pre $a,b \neq 0$ platí $\overline{(a,b)}^{-1} = \overline{(b,a)}$ . Celému číslu a odpovedá racionálne číslo $\overline{(a,1)}$ .

Reálne čísla

Konštrukcia reálnych čísiel je trochu zložitejšia, preto tu nebudem uvázdať celý postup. Je nutné definovať usporiadanie na množinách Z a Q a následne definovať operácie pomocou rezov množiny Q. R definujeme ako množinu všetkých rezov, ktoré sú buď mezery (iracionálne čísla) alebo dedekindovské rezy 1.druhu (racionálne čísla). Viac informácií nájdete v skriptách ⁹⁾.

Komplexné čísla

Množinu komplexných čísel C chápeme ako množinu všetkých dvojíc reálnych čísel, teda $C = R \times R$ . Pre ľubovoľné $(a,b),\ (c,d)\in C$ definujeme operácie sčítania a násobenia:

$(a,b)+(c,d) = (a+c,b+d)$

$(a,b)\cdot (c,d) = (ac-bd,ad+bc)$

Ak komplexné číslo (0,1) označíme i a (t,0) t, môžeme každé komplexné číslo $z= (a,b)$ písať v tvare:
$z= a+bi$ (algebraický tvar, a - reálna časť, b -imaginárna časť)
Pre imaginárnu jednotku platí $i^2 = -1$ , to nám dovoľuje riešiť aj také rovnice (napr. $x^2 + 1= 0$ ), ktoré v obore reálnych čísel nemajú riešenie.
Z algebraického tvaru a ze vztahu $i^2 = -1$ pak můžeme zpětně rekonstruovat násobení komplexních čísel: $(a,b)\cdot(c,d) = (a+bi)\cdot(c+di) = ac-bd + adi+bci = (ac-bd, ad+bc)$

Co byste ještě měli znát?

Měli byste chápat a být schopni vysvětlit rozdíl mezi minimálním a nejmenším prvkem.
Měli byste být schopni sami uvést příklady svazu, úplného svazu nebo nelineárního uspořádání.
Ale také byste měli být schopni určovat supréma, infima pro množiny zadané komisí a měli byste umět určit, zda je daná množina svaz, úplný svaz apod.

Predmety

FI:MB005 Základy matematiky (podzim 2005), Mgr. Ondřej Klíma, Ph.D.
FI:IB000 Úvod do informatiky (podzim 2005), prof. RNDr. Antonín Kučera, Ph.D.

Použitá literatúra

skriptá Úvod do informatiky, prof. RNDr. Antonín Kučera, Ph.D. (odkaz som nenašiel)
Mgr. Jan Holeček riešené príklady 6.sada (dostupné pouze z domény muni.cz)
Učebné materiály k MB005
Uspořádání, skripta pro ÚdoI, doc. RNDr. Petr Hliněný, Ph.D.

Vypracoval

Dušan Katona, ICQ: 426 081 873, snad do 27.5
hotovo: <99%>
môžete kluďne niečo doplniť alebo opraviť

Otázku si přečetl pan RNDr. Jan Bouda a rámcově prošel. Jeho podněty pro doplnění textu, opravy nesrovnalostí a odstranění matoucích či k otázce se nevztahujících textů byly do otázky zaneseny. Tato kontrola je jen rámcová, stále se může stát, že v otázce zůstala zapomenutá chybka či nesrovnalost, vyučující za toto nenese odpovědnost, berte tuto rámcovou kontrolu jako formu pomoci od vyučujících pro studenty.

¹⁾

Základy matematiky skriptá, str. 13

²⁾

riešené príklady od Mgr. Jana Holečka, 6. sada

³⁾

www.cam.zcu.cz/~ryjacek/students/DMA/skripta/3.pdf

⁴⁾

Základy matematiky skriptá, str. 14

⁵⁾

http://user.mendelu.cz/marik/in-mat-web/in-mat-webse18.html

⁶⁾

skriptá RNDr. Pavla Horáka

⁷⁾

Algebra v obrázcích - http://algebra.matfyz.info/

⁸⁾

Základy matematiky skriptá, str. 12

⁹⁾

Základy matematiky skriptá, str.17

Diskuze

Petr Kott, 2008/06/03 15:22

Chapu dobre, ze nejmensi prvek je mensi nez VSECHNY ostatni, a tak znamenko < neznamena „mensi rovno“, ale je symbolem pro usporeadani…

Petr Kott, 2008/06/03 17:01

Jeste jedna otazecka… co je ta ekvivalence Z v celych cislech ze Zo do Zo. Respektive Q v racionalnich.. nejak jem to nepobral. Dik

Dusan Katona, 2008/06/03 20:38

ano, najmensi prvok musi byt porovnatelny a byt mensi so vsetkymi ostatnymi, aby bol najmensi
ta relace ekvivalence ti urcuje, kedy su tie prvky „rovnake“, aby si mohol nasledne spravit rozklad mnoziny…teda pri Q, mas ad = cb pre zlomky a/b a c/d –> napr 1/2 a 2/4 ti dava 1*4 = 2*2, preto su 1/2 a 2/4 v relaci a patria do rovnakej faktorovej mnoziny rozkladu Q

Petr Kott, 2008/06/04 11:16

jaaj, chapu.. dik

Zdeněk Kedaj, 2008/06/08 01:42

chybi mi tu komplexni cisla

Dusan Katona, 2008/06/08 10:11

mozem ich sem doplnit, ale len definiciu, konstrukciu komplexnych cisel sme sa nikde neucili…

Zdeněk Kedaj, 2008/06/09 17:42

myslim ze by tam mely byt zmineny. Podle me by stacilo ze nosna mnozina je R x R a ze maji realnou a imaginarni cast, ze lze provest odmocninu z -1

Dusan Katona, 2008/06/09 22:28

doplnil som, ak nieco este chyba, mozes to kludne doplnit :)

Roman Plášil, 2008/06/20 22:18

Definice a konstrukce jsou v Algebře 1. Je to faktorové těleso $\mathbb{R}[x]/_{(x^2 + 1)}$ neboli polynomy nad reálnými čísly podělené ideálem x^2 + 1. Jinými slovy, jsou to polynomy nad reálnými čísly, které jsou stupně menšího než 2. Navíc právě tento polynom má řešení, jímž je polynom x neboli imaginární jednotka. No ale věřím, že tohle po nás nebudou chtít.

Radim Čebiš, 2008/06/11 14:09

Ten obrazek Hasseovskeho diagramu lexikografického urporadani je IMHO spatne… Lexikograficky by mela byt „dlouha cara“. Tzn. prvek (b1,a1) nad nim (b1,a2) nad nim (b1,a3) nad nim (b1,a4) nad nim (b2,a1) nad nim (b2,a2) atd.
Jestli je ma uvaha spravna a jestli nekdo umite ty diagramy kreslit, tak ho tam vymente.
diky

Tomáš Hanáček, 2008/06/11 17:18

Myslím, že je správně, lexikografické uspořádání kopíruje tvar té množiny A dvakrát nad sebou, nemůže to být čára, některé prvky jsou neporovnatelné.

Radim Čebiš, 2008/06/11 21:21

Samozrejme mas pravdu…, nejak mi nedoslo, ze jsou to vlastne ty mnoziny, co jsou kresleny vejs…

Winsik, 2008/06/13 15:55

tady jsem nasel popis ciselnych oboru pro trouby jako jsem ja … http://cs.wikipedia.org/wiki/%C4%8C%C3%ADslo#.C4.8C.C3.ADseln.C3.A9_obory

je tam i dobry obrazek jak se mnoziny vlastne doplnuji.

Nepridat to i sem?

Dusan Katona, 2008/06/13 21:11

jj ten obrazok sa hodi, mozes ho sem pridat :)

Michal Ďurec, 2008/06/14 21:37

Ahoj, mam pripomienku k „svazom“ - specialne pripady.
Oproti skriptam zo zakladov matematiky si pouzil ine oznacenie mnozin, co vedie k mylnej predstave o tom, co je sup(0) a inf(0), (0) som oznacil prazdnu mnozinu. Odkazujes na mnozinu A (sice pisane inym fontom, ale to je jedno…), ktora ma v texte predtym iny vyznam, nez v skriptach. Teda aspon podla mna navazuje text v skriptach na predoslu definiciu mnoziny A. Ak je tak, v tomto texte by sa malo pisat o mnozine M. Skontroluj, prosim, ci je to tak a sprav pripadne potrebne zmeny :)

PS1: To iste sa tyka aj nasledujuceho textu az po vetu 1.
PS2: Oznacenie P(A) je, predpokladam, pre potencnu mnozinu mnoziny A. Aj toto je vhodne doplnit, lebo v inych textoch sa potencna mnozina oznacuje 2(umocnene na)A. Na tychto strankach som zatial na oznacenie P(A) inde nenarazil..

Dusan Katona, 2008/06/15 09:59

Tie specialne pripady mali byt oddelene od predosleho textu, cize A mala byt ina mnozina…ale mas pravdu, moze to byt matuce, preto to opravim na M. Ohladom toho fontu: nechcelo sa mi to vsetko uzatvarat do tagov <math>, som lenivy :) ak to vadi, tak to oprav…
Ohladom P(A): ja som sa pocas svojho studia stretaval hlavne s tymto oznacenim, doplnim to tam ale, ze to je potencna mnozina…
Dik za pripomienky :)

Dusan Katona, 2008/06/15 11:43

Ked to tu uz upravujete, tak si budte na 100% isty, ze to je spravne:
Niekto upravil tvrdenie, ze “(Z*,|) nie je usporiadana mnozina“ na tvrdenie “(Z*,|) nie je _linearne_ usporiadana mnozina“, to je sice pravda, ale to mimo ineho znamena, ze (Z*,|) je usporiadana, len nie linearne. To ale nie je pravda, pretoze | na Z* nie je antisymetricka:
4|-4 a -4|4 → 4 sa nerovna -4

Pavel Koudela, 2008/06/15 13:41

Nechci vnest zmatky proto se radsi ptam:

svaz = kazda neprazdna konecna mnozina musi mit sup a inf
uplny svaz = kazda mnozina musi mit sup a inf

a dvojprvkovych mnozinach by nemela byt vubec rec, mam pravdu?

Marek Babák, 2008/06/15 14:48

Co jsem se díval do různých zdrojů, tak při svazu se skutečně mluví o dvojprovkové. Nicméně, když se nad tím zamyslíš, tak zjistíš, že to co jsi napsal ty, je ekvivalentní tomu jak je to napsáno, vzhledem k vlastnostem uspořádání(když má sup(A,B), sup(B,C) a sup(A,C) ⇒ tak má i sup(A,B,C)). Nejsem si jistý, jak je to s podmínkou naprázdnosti, imho musí být jak u svazu, tak u úplného svazu(co je sup. prádzné množiny?). Jestli se v něčem pletu, tak mě prosím opravte.

Dusan Katona, 2008/06/15 14:58

supremum a infimum prazdnej mnoziny je popisany v tych specialnych pripadoch - je to najmensi a najvacsi prvok usp. mnoziny, ak existuje…svaz ale nemusi mat najmensi alebo najvacsi prvok (uplny svaz musi), aby bol svaz (priklad teraz nestvorim, ale nejaky existuje urcite :) )
inak dik za super obrazok k tym svazom :)

Michal Ďurec, 2008/06/17 13:38

tie obrazky su sice super, ale bud je tam chyba v zapise a < b < b < e < g < j (zjednodusene, len znak <), alebo tomu vobec nerozumiem :) preco su tam len tieto prvky, preco nie aj ine… a preco je tam b dvakrat?? snad sa najde niekto, kto to chape :) vdaka

Dusan Katona, 2008/06/18 16:55

Ja som si to vobec nevsimol, v tom zapise je urcite chyba…aj tak tam ide len o urcenie suprem/infim z toho Hasseovskeho diagramu. A ten H.D. je podla mna v pohode citatelny (to ako su jednotlive prvky usporiadane, si urcite vyvodis sam :) )

Roman Plášil, 2008/06/20 22:20

Dobrý příklad svazu, jež není úplný svaz jsou celá čísla. Každá dvojprvková (a tedy i konečná) množina má supremum a infimum, jenže nekonečné množiny to nemají.

Dusan Katona, 2008/06/20 22:30

Podla mna $(P(N),\subseteq)$ je uplny svaz a pritom P(N) je nekonecna…pri usporiadani podla velkosti klasickych mnozin N,Z.. samozrejme plati, co si napisal…

Dusan Katona, 2008/06/15 14:42

Pojmy kazda neprazdna konecna podmnozina a kazda dvojprvkova mnozina su vzajomne zamenitelne (je to nakoniec napisane aj v tych dosledkoch pod tou vetou), toto som myslim citoval zo skript RNDr. Pavla Horáka, tam je to uvedene takto. V skriptach Zakladov matematiky to najdes tiez (neviem ako v Matematike v apl.informatike)
Je to asi z toho dovodu, ze sa to lahsie potom dokazuje (vid priklad (N,|))…

Ondřej Božek, 2008/06/20 12:52

Neměla by u těch nejmenších, největších, maximálních a minimimálních prvků být ta množina (A,<) předusporádání misto uspořádání? Napřiklád definice minimálního resp. maximálního prvku používá symetrii - y<x ⇒ x<y .

Marek Babák, 2008/06/20 15:01

řekl bych, že ne, podle toho jak to chápu - u kvaziuspořádání si mohou být dva prvky rovny(může tam být symetrie), kdežto u uspořádání ne(je tam požadavek na antisymetrii). Maximální prvky splňují tu definici která tam je, ale navzájem mohou být neporovnatelné(nikoliv si rovné). Ta definice maximálního prvku je tam divně, to jsem si taky říkal, já ji radši píšu takhle:
“(A,>= ) je usp. Řekneme, že prvek x množiny A je maximální ⇔ neexistuje y!=x takové, že y>=x“

Dusan Katona, 2008/06/20 17:15

k tym definiciam max. a min prvkov:
Je to opisane zo slidov Uvodu do informatiky, takze je to v poriadku :) Vysvetlenie, napr. minimalny prvok (obdobne pre maximalny)
ak existuje prvok y, ktory je mensi ako x ⇒ (x = y) (lava a prava strana implikacie nam davaju $y \leq x \wedge x \leq y$ , z coho vyplyva, ze x = y).
Lepsie je asi pouzit tu definiciu v zatvorke, ako vravim, v Uvode do inf. to bolo uvedene takto, preto som to sem radsej napisal uplne presne.

KsR, 2009/06/08 15:19

Tak úplně nerozumím „větě 1“ - chápu dobře, že libovolná podmnožina uspořádané množiny A má infimum?
A co třeba množina {a,b,c}, kde: a<b, a<c. Taková množina je uspořádaná, ale podmnožina {a} nemá supremum (protože prvky b,c nelze porovnat)… Může mi to prosím někdo objasnit?

KsR, 2009/06/08 17:25

už to chápu - jestliže libovolná podmnožiny uspoř. množiny má infimum, pak má libovolná podmnožina i supremum (a naopak) - omlouvám se za „špatný“ dotaz :)

Stefan Sakalik, 2011/01/22 16:53

Podla mna „veta 1“ neplati. Tvoja mnozina {a,b,c}, kde: a<b, a<c ma infimum pre kazdu podmnozinu. Ale napriklad mnozina {a,b,c} (ona je tiez podmnozinou {a,b,c}) nema supremum. Btw mnozina {a} ma napriklad supremum b.

Pavel Smolka, 2011/06/19 15:52

Souhlasím s neplatností věty 1, dalším příkladem mohou být přirozená čísla (třeba s nulou):

Libovolná podmnožina N má infimum (buď je to nula nebo nejmenší číslo té podmnožiny).
Libovolná podmnožina N NEmá supremum - konkrétně celá množina přirozených čísel nemá supremum (resp. má, ale ne v množině přirozených čísel). - Zdroj: http://cs.wikipedia.org/wiki/Supremum

Vojtěch Havel, 2012/06/12 14:02

Veta 1 platí.

Tento protipříklad {a,b,c}; a<b, a<c nefunguje, protože není pravda, že každá jeho podmnožina má infimum.
Neexistuje totiž inf{} (infimum prázdné množiny), to by mělo být rovno největšímu prvku (protože lib. prvek je také dolní závorou prázdné množiny), ale takový prvek v {a,b,c} neexistuje.

Stejně tak není pravda, že libovolná podmnožina N má infimum - prázdná množina je opět protipříkladem.

Fanda Blahoudek, 2009/06/16 09:02

Ahoj, mám 2 dotazy:
1) nějak mi uniká význam té věty 1: Množina A, která je jako příklad Hasseovských diagramů, obsahuje infimum pro každou svoji podmnožinu, ale pro {a3,a4} nelze najít supremum. Nebo to funguje nějak jinak?

2) Svazové operace ∧ a ∨ jsou infimum a supremum?

Fanda Blahoudek, 2009/06/16 09:05

Ad 1) Znamená to, že inf i sup musí být prvky A? Pokud ano, tak už tomu rozumím.

Fanda Blahoudek, 2009/06/16 09:12

Ad 2) Ano :-)

You could leave a comment if you were logged in.

home/inf/ap3.txt · Poslední úprava: 2020/04/12 16:56 (upraveno mimo DokuWiki)

Nahoru