Obsah
N-AP15
Zadání
Rekurzivní a rekurzivně spočetné jazyky. Turingovy stroje. Pojem nerozhodnutelnosti a částečné rozhodnutelnosti.
Rekurzivní a rekurzivně spočetné jazyky
Definice
- rekurzivně spočetný ⇔ L = L(M) pro nějaký Turnigův stroj M
- rekurzivní ⇔ L = L(M) pro nějaký úplný Turnigův stroj M
Ke každému rekurzivnímu jazyku L existuje Turingův stroj, který ho rozhoduje, tj. výpočet na každém vstupním slovu je konečný. Rekurzivně spočetný jazyk musí splňovat slabší podmínku: musí pro něj existovat Turingův stroj, který ho akceptuje, tj. akceptuje každé slovo z L, ale výpočet na slovu nepatřícím do L může být bud’ zamítající, nebo nekonečný.
Mezi rekurzivní jazyky patří regulární, bezkontextové, kontextové jazyky a další jazyky, které splňují podmínku rekurzivního jazyka. Každý rekurzivní jazyk je i rekurzivně spočetný (opačně to neplatí). Rekurzivně spočetné jazyky se dají generovat gramatikami typu 0. Metodou diagonalizace se dá dokázat, že existuje jazyk, který není rekurzivně spočetný.
S rekurzivními a rekurzivně spočetnými množinami úzce souvisí rozhodnutelné, nerozhodnutelné a částečně rozhodnutelné problémy:
Problémy
- rozhodnutelný – právě když množina všech řetězců, která má vlasnost P, je rekurzivní
- nerozhodnutelný – právě když není rozhodnutelný
- částečně rozhodnutelný – právě když množina všech řetězců, která má vlastnost P, je rekurzivně spočetná
Uzávěrové vlastnosti rekurzivních a rekurzivně spočetných jazyků
Věta
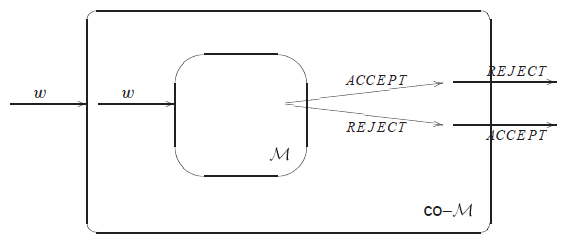
Důkaz pro sjednocení
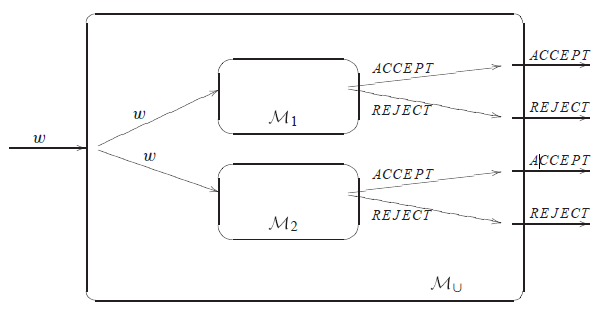
Důkaz pro průnik
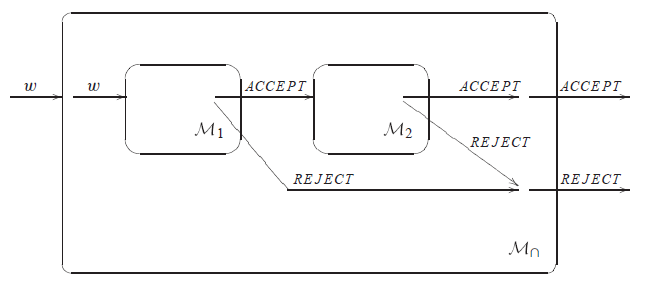
Důkaz pro zřetězení
Nedeterministický stroj M∗, akceptující L1∗, je zobecněním stroje M·.
Věta
Postova věta
Důkaz
Důsledkem Postovy věty je, že třída rekurzivně spočetných jazyků není uzavřená na komplement. Pokud by platil opak, třídy rekurzivních a rekurzivně spočetných jazyků by se rovnaly.
Turingovy stroje
Definice
je konečná množina stavů
je konečná množina vstupních symbolů
je konečná množina páskových (pracovních) symbolů, obsahující jako svou podmnožinu abecedu
je levá koncová značka
je symbol označující prázdne políčko
je totální přechodová funkce
je počáteční stav
je akceptující stav
je zamietající stav
Turingův stroj má konečnou množinu stavů Q, pásku, která je rozdělena na jednotlivá políčka, a hlavu, která se může po pásce pohybovat doleva a doprava, číst a zapisovat symboly. Na každém políčku pásky je zapsán právě jeden z konečně mnoha páskových (pracovních) symbolů. Páska je jednosměrně nekonečná. Na nejlevějším (nultém) políčku je zapsán speciální symbol , označující levý konec pásky. Na začátku výpočtu je na prvním až n-tém, n ≥ 0, políčku pásky zapsán vstupní řetěz (vstupem tedy může být i prázdný řetěz). Ostatních nekonečně mnoho políček napravo od vstupu je prázdných — tuto skutečnost vyjádříme pomocí speciálního znaku
. Výpočet začíná v počátečním stavu q0, přičemž hlava snímá nulté políčko obsahující levou koncovou značku
. Krok výpočtu spočívá v tom, že stroj v závislosti na momentálním stavu a symbolu snímaném hlavou
- změní svůj stav (či přesněji může změnit),
- zapíše symbol na políčko snímané hlavou (čímž přepíše symbol, který tam byl zapsán předtím) a
- posune hlavu o jedno políčko doprava, nebo doleva.
Způsob, jakým se má změnit stav, přepsat symbol a posunout hlava, předepisuje přechodová funkce δ. Stroj akceptuje vstupní řetěz, právě když přejde do speciálního akceptujícího stavu qaccept. Stroj zamítá právě když přejde do speciálního zamítajícího stavu qreject. Na některých vstupech může výpočet běžet nekonečně dlouho, aniž by stroj vstupní slovo akceptoval, nebo zamítnul. V takovém případě říkáme, že stroj pro daný vstup cyklí. 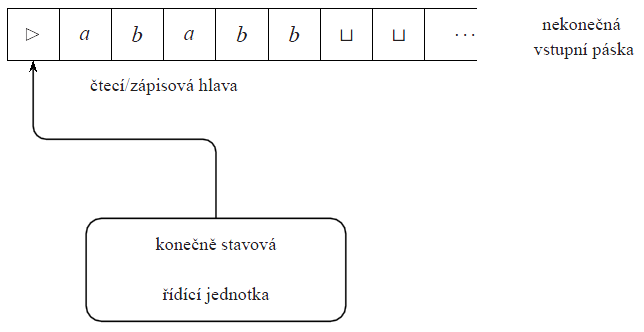 Navíc požadujeme, aby Turingův stroj nikdy nepřepsal levou koncovou značku jiným symbolem a aby nikdy neposunul svou hlavu vlevo od políčka obsahujícího levou koncovou značku. Formálně, požadujeme aby pro každé
Navíc požadujeme, aby Turingův stroj nikdy nepřepsal levou koncovou značku jiným symbolem a aby nikdy neposunul svou hlavu vlevo od políčka obsahujícího levou koncovou značku. Formálně, požadujeme aby pro každé existoval stav
takový, že:
Pojem nerozhodnutelnosti a částečné rozhodnutelnosti
Problém, kdy se má určit, zda řetěz w má vlastnost P, nazýváme:
- rozhodnutelný právě když množina všech řetězů majících vlastnost P je rekursivní, tj. existuje úplný Turingův stroj M, který akceptuje každý řetěz mající vlastnost P a zamítne každý řetěz, který tuto vlastnost nemá (M rozhoduje jazyk obsahující právě všechna ta slova, která mají vlastnost P);
- nerozhodnutelný právˇe když není rozhodnutelný;
- částečně rozhodnutelný (semirozhodnutelný) právě když množina všech řetězů majících vlastnost P je rekursivně spoěetná, tj. existuje Turingův stroj, který akceptuje každý řetěz mající vlastnost P (a zamítá anebo cyklí pro řetěz nemající vlastnost P).
Namísto ”problém určit, zda řetěz w má vlastnost P je rozhodnutelný (částečně rozhodnutelný)“ zkráceně říkáme, že vlastnost P je rozhodnutelná resp. že problém P je rozhodnutelný (částečně rozhodnutelný). Ačkoli vlastnost rekursivní resp. rekursivně spočetný vypovídá o množinách, zatímco rozhodnutelnost resp. semirozhodnutelnost je vlastnost problémů, jsou oba pojmy úzce spjaty.
Platí mezi nimi tato ekvivalence:
P je rozhodnutelný ⇔ jazyk {w | w má vlastnost P} je rekursivní
L je rekursivní ⇔ problém ”w?∈L“ je rozhodnutelný
P je semirozhodnutelný ⇔ jazyk {w | w má vlastnost P} je rekursivně spočetný
L je rekursivně spočetný ⇔ problém ”w?∈L“ je semirozhodnutelný
Předměty
IB102 Automaty a gramatiky
IB005 Formální jazyky a automaty
Vypracoval
Marek Menšík UČO 255679
Nevím přesně, kdo otázky zpracoval přede mnou, pouze jsem je sem umístil, doplnil chybějící věci a opravil nepřesnosti. Připomínám, že věci zde uvedené nemusí být korektní a zatím neprošly kontrolou žádného z profesorů. Z mé strany je tato otázka dokončena a případné chybějící věci a chyby mě můžete napsat na UČO mail nebo se registrujte a upravte je sami.
Z mě strany prozatím hotovo
Možná by se u nerozhodnutelných problémů dalo doplnit více věcí jako Postův korespondenční problém, diagonalizace a jiné.