Obsah

AP12 Pravděpodobnost a statistika
Diskuze

AP12 Pravděpodobnost a statistika

(klasická a podmíněná pravděpodobnost, distribuční funkce a rozdělení náhodných veličin, výpočet střední hodnoty, rozptylu a kovariance)

Pravděpodobnost náhodného jevu je číslo, které je mírou očekávatelnosti výskytu jevu. ¹⁾ (Popisná) statistika je zpracování číselných dat o nějakém souboru objektů.
Matematická statistika je věda aplikovaná na problémy spojené se sběrem a pozorováním náhodných dat.

Terminologie

$\Omega$ = množina všech možných výsledků, základní prostor. Prvky $\omega \in \Omega$ představují jednotlivé možné výsledky.

Jevové pole je systém podmnožin $\Delta$ základního prostoru uzavřený na konečné průniky, spočetná sjednocení a množinové rozdíly. Jednotlivé množiny $A \in \Delta$ nazýváme náhodné jevy (vzhledem k $\Delta$ ).

Základní pojmy

jistý jev je celý základní prostor $\Omega$
nemožný jev je prázdná podmnožina $\emptyset \in \Delta$
elementární jevy jsou jednoprvkové podmnožiny $\{\omega\}, \omega \in \Omega$
společné nastoupení jevů $A_{i}, i \in I$ je jejich průnik, tedy odpovídá jevu $\bigcap_{i \in I}{}{} A_{i}$ ,
nastoupení alespoň jednoho z jevů $A_{i}, i \in I$ je jejich sjednocením, odpovídá jevu $\bigcup_{i \in I}{}{} A_{i}$
neslučitelné jevy $A,B \in \Delta$ jsou jevy, pro které platí $A \cap B$ = $\emptyset$
jev A má za důsledek jev B, když $A \subset B$
opačný jev k jevu A je jev $B = \Omega \backslash A$ , píšeme $B = A^c$

Pravděpodobnostní funkce je funkce $P : \Delta \rightarrow R$ na jevovém poli $(\Omega,\Delta)$

Vlastnosti pravděpodobnostní funkce

je nezáporná, tj. $P(A) \geq 0$ pro všechny jevy $A$ ,
je aditivní, tj. $P\left(\bigcup_{i \in I}{}{} A_{i}\right) = \sum_{i \in I} P(A_{i})$ , pro každý nejvýše spočetný systém po dvou neslučitelných jevů (laicky: „dá se sčítat, když jsou jevy neslučitelné“),
pravděpodobnost jistého jevu je 1.
pravděpodobnost opačného jevu je $P(A^c) = 1 - P(A)$

Pravděpodobnosti

Rozlišujeme dvě definice pravděpodobností: klasickou a geometrickou. Pokud klademe podmínky, bavíme se o tzv. podmíněné pravděpodobnosti.

Klasická pravděpodobnost

Klasická pravděpodobnost je pravděpodobnostní prostor $(\Omega, \Delta, P)$ s pravděpodobnostní funkcí $P : \Delta \rightarrow R,$
$P(A) = \frac{{|}A{|}}{{|}\Omega{|}}$ .

Jednoduchý príklad

Zadanie: Hádžeme kockou. Aká je pravdepodobnosť, že hodíme číslo 6?

Riešenie:

${|}A{|}$ - úspešný výsledok (hodená 6)
${|}\Omega{|}$ - všetky možné výsledky (1 až 6)

$P(A) = \frac{{|}A{|}}{{|}\Omega{|}} = \frac{1}{6} = 0,166666667 = 17\%$ .

Geometrická pravděpodobnost

Zde je definice pravděpodobnosti založena na porovnání objemů, ploch či délek geometrických útvarů.
$P(A) = \frac{vol\ A}{vol\ \Omega}$

Příklad - jen nastínění řešení

Zadání: Romeo a Julie si smluvili schůzku mezi 12:00 a 13:00. Přijdou náhodně v tomto rozmezí a čekají na sebe 20 minut, nejdéle však do 13:00. Jaká je pravděpodobnost, že se setkají?

Nástin řešení: musíme si vytvořit funkci, která nám v pravděpodobnostním prostoru odděluje jev příznivý od nepříznivého. Potom spočítáme obsah části, která znázorňuje jev příznivý a dělíme obsahem celého prostoru.

Podmíněná pravděpodobnost

Nechť H je jev s nenulovou pravděpodobností v jevovém poli $\Delta$ v pravděpodobnostním prostoru $(\Omega, \Delta, P)$ . Podmíněná pravděpodobnost $P(A|H)$ jevu $A \in \Delta$ vzhledem k hypotéze H je definována vztahem $P(A|H) = \frac{P(A \cap H)}{P(H)}$ (napr. „jaká je pravděpodobnost, že při hodu dvěmi kostkami padly dvě pětky, je-li součet hodnot deset?“).

Pravděpodobnost průniku a sjednocení jevů

Definice odpovídá požadavku, že jevy A a H nastanou zároveň, za předpokladu, že A nastal s pravděpodobností $P(A \cap H)/P(A)$ .

Je také vidět přímo z definice, hypotéza H a jev A jsou nezávislé tehdy a jen tehdy, je-li $P(A) = P(A|H)$ .

Přepsáním formule pro podmíněnou pravděpodobnost dostáváme

$P(A \cap B) = P(B \cap A) = P(A)P(B|A) = P(B)P(A|B)$

$P(A \cup B) = P(A) + P(B) - P(A\cap B)$ … závislé
$\ \ \ \ \ \ \ \ \ \ \ \ \ = P(A) + P(B)$ … nezávislé

$P(A \cap B) = P(A|B) \cdot P(B)$ … závislé
$\ \ \ \ \ \ \ \ \ \ \ \ \ = P(A) \cdot P(B)$ … nezávislé
obecně: $P(A_{1}\cap A_{2} \cap ... \cap A_{n})= P(A_{1}) \cdot P(A_{2}|A_{1}) \cdot .. \cdot P(A_{n}|A_{1} \cap A_{2} \cap ... \cap A_{n})$

Bayesův vzorec Pro pravděpodobnost jevů A a B platí
$P(A|B) = \frac{P(B|A) P(A) }{P(B)}$

Využíváme jej, když známe podmíněnou pravděpodobnost P(B|A) a chceme zjistit P(A|B).

Jednoduchý příklad

Zadání: Dva střelci vystřelí každý jednu ránu na terč. První má pravděpodobnost zásahu 80%, druhý 60%. V terči se našla jedna rána. Jaká je pravděpodobnost, že patří prvnímu střelci?

Řešení: $P(H_{1})= 0,8$ , $P(H_{2})= 0,6$ Jev A: rána patří prvnímu střelci
Pravděpodobnost toho, že se trefí první střelec = (pravděpodobnost, že se první trefí a druhý ne) / (pravděpodobnost, kdy je v terči 1 rána)

Pravděpodobnost, kdy je v terči 1 rána: $0.8\cdot 0.4 + 0.2\cdot 0,6 = 0,44$ (bud se prvni trefi a druhy ne a nebo naopak)
$P(A) = \frac{0,8\cdot 0,4}{0,44}$ ²⁾.

Distribuční funkce a rozdělení náhodných veličin

Nahodná veličina –- zavádíme ji, protože chceme pracovat s intervaly – vyjádřit, jaká je pravděpod., že daná hodnota bude právě z tohoto intervalu.
Rozdělení pravděpodobnosti je pravidlo, které přiřazuje pravděpodobnosti událostem nebo tvrzením.
Existuje několik způsobů, jak vyjádřit rozdělení pravděpodobnosti. Nejobvyklejší je uvést hustotu rozdělení pravděpodobnosti; samotná pravděpodobnost jevu se pak získá integrací funkce hustoty.
Diskrétní rozdělení pravděpodobností (definováno na spočetné, diskrétní množině, jako je podmnožina celých čísel) - např. binomické, Poissonovo
Spojité rozdělení (existuje spojitá distribuční funkce, např. polynomická nebo exponenciální) - např. normální rozdělení, exponenciální rozdělení ³⁾

Distribuční funkce

distribuční funkcí náhodné veličiny X je funkce $F : R \rightarrow R$ definovaná pro všechny $x \in R$ vztahem
$F(x) = P(X \leq x)$

Diskrétní náhodná veličina X

X na pravděpodobnostním prostoru $(\Omega, A, P)$ nabývá jen konečně mnoha hodnot $x_{1}, x_{2}, . . . , x_{n} \in R$ . Pak existuje tzv. pravděpodobnostní funkce f(x) taková, že
$f(x) = P(X = x_{i}) x = x_{i}\ ;\ 0\ jinak.$ Evidentně $\sum_{i=1}^{n}\ f(x_{i}) = 1$ a pro rozdělení pravděpodobnosti platí
$P(X^{-1} B) =\sum_{x_{i} \in B}\ f(x_{i})$ a tedy zejména je distribuční funkce tvaru
$F_{X}(t) =\sum_{x_{i} \leq t}\ f(x_{i})$ Každá náhodná veličina definovaná pro klasickou pravděpodobnost je diskrétní.

Diskrétní veličinu si můžeme představit jako graf složený z bodů, které odpovídají pravděpodobnosti daného jevu (pro házení kostkou je to 1/6)

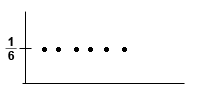Sečtení hodnot bodů musí dát 1.
Distribuční funkce $F_{X}$ v bodě 3 se vlastně rovná součtu pravděpodobnostních hodnot do tohoto bodu, tedy $\frac{1}{6} + \frac{1}{6} + \frac{1}{6}$

Spojité náhodné veličině odpovídá spojitá distribuční funkce.
$F(x) = P(A \leq X \leq B) = \int_{a}^{b} f(x) dx$ , kde f(x) je funkce hustoty pravděpodobnosti.

Funkce hustoty pravděpodobnosti

Nechť X je náhodná veličina, F(x) je její distribuční funkce.

F je zleva spojitá, $lim_{x \rightarrow -\infty} = 0$ a $lim_{x \rightarrow \infty} = 1$ .
Vždy platí $P(a \leq X < b) = F(b) - F(a)$ .
Je-li X diskrétní s hodnotami $x_{1}, . . . , x_{n}$ , pak je F(x) po částech konstantní, $F(x) = \sum_{x_{i} \leq x}\ P(X = x_{i})$ a $F(x) = 1$ kdykoliv $x > x_{n}$ .
Je-li X spojitá, pak je F(x) diferencovatelná a její derivace se rovná hustotě pravděpodobnosti X, tj. platí

$F'(x) = f(x)$ .

Spojitou veličinu si můžeme představit jako spojitý graf (když například zobrazujeme výšku lidí)

Plocha pod křivkou musí mít obsah 1.
Distribuční funkce $F_{X}$ se proto vyjadřuje jako integrál.

Rozdělení náhodných veličin

Diskrétní

sem patří degenerované rozdělení, alternativní rozdělení, binomické rozdělení, Poissonovo rozdělení

Degenerované rozdělení

$Dg(\mu)$ – konstantní hodnota $X = \mu$
distribuční funkce: $F_{X}(t) = 0$ pro $t \leq \mu$ ; 1 pro $t > \mu$
pravděpodobn. funkce: $f_{X}(t) = 1$ pro $t = \mu$ ; 0 jinak

Alternativní rozdělení

A(p) – popisuje pokus s pouze dvěma možnými výsledky (zdar nebo nezdar), pravděpodobnosti jsou p a (1-p):
$F_{X}(t) = 0$ pro $t \leq 0$ ; $1-p$ pro $0 < t \leq 1$ ; 1 pro $t > 1$
$f_{X}(t) = p$ pro $t = 1$ ; $1-p$ pre $t = 0$ ; 0 jinak

Binomické rozdělení

$Bi(n, p)$ – odpovídá n–krát nezávisle opakovanému pokusu popsanému alternativním rozdělením, přičemž naše náhodná veličina měří počet zdarů.
$f_{X}(t) = {n \choose t}\ p^{t}\ (1 - p)^{n-t}$ pro $t \in {0, 1, . . . , n}$ ; 0 jinak
nejvíce výsledků bude blízko hodnoty np

Příklad s nastíněným řešením

Zadání: Pravděpodobnost narození chlapce je 0,515. Jaká je pravděpodobnost, že mezi deseti tisíci novorozenci bude stejně nebo více děvčat než chlapců?

Řešení: $P(p) = 0,515$ , $n = 10000$

Protože se vlastně nezávisle stále opakuje „pokus“ s výsledkem „kluk“ nebo „děvče“, použijeme Binomické rozdělení Bi(n,p), tedy Bi(10000; 0,515).

$Y_{10000} \sim Bi(10000; 0,515)$

$P(Y_{10000}=x) = {n \choose k}\ p^{t}\ (1 - p)^{n-t}$ …dosadíme 10000 za n

$P(Y_{10000}=5000)=$ dosadíme do vzorce

$P(Y_{10000}\leq 5000)= \sum_{x=0}^{5000} \ldots$

Poissonovo rozdělení

$Po(\lambda)$ – dobře aproximuje binomická rozložení $Bi(n, \lambda/n)$ pro konstantní $\lambda > 0$ a veliká n:
$f_X(t) = \left(\frac{\lambda^{t}}{t!}\right) e^{-\lambda}$ pro $t \in N$ ; 0 jinak

Spojité

sem patří rovnoměrné rozdělení, exponenciální rozdělení, normální rozdělení

Rovnoměrné rozdělení

* R(a, b) -– hustota $f_{X}(t)$ je konstantní na daném intervalu, jinde je 0

$f_{X}(t) = 0$ pro $t \leq a$ ; $\frac{1}{b-a}$ pro $t \in (a, b)$ ; 0 pro $t \geq b$
$F_{X}(t) = 0$ pro $t \leq a$ ; $\frac{t-a}{b-a}$ pro $t \in (a, b)$ ; 1 pro $t \geq b$ ,

Exponenciální rozdělení

$ex(\lambda): F_{X}(t) = 1 - e^{-\lambda t}$ pro $t > 0$ ; 0 pro $t \leq 0$ .
$f_{X}(t)= \lambda e^{-\lambda t}$ pro $t > 0$ ; 0 pro $t \leq 0$ .

Normální rozdělení

hustota $f_{X}(x) = \left(\frac{1}{\sqrt{2\pi}}\right)\ e^{-\frac{x^2}{2}}\ =\$ Gaussova křivka – rozdělení s touto hustotou se nazývá normální rozdělení N(0,1) (první parametr střední hodnota, druhý rozptyl)
binomické B(n,p) pro velké n konverguje k normálnímu N(np, np(1 − p))
$F_{X}(x)= \int_{-\infty}^{\infty} e^{\frac{-x^{2}}{2}} dx$

Výpočet střední hodnoty, rozptylu a kovariance

Výpočet střední hodnoty

při rovnoměrném rozdělení je střední hodnotou aritmet. průměr
pro diskrétní veličinu: $EX = \sum_{i}\ x_{i} f_{X}(x_{i})$ - hodnotu vždy vynásobím hodnout její hustoty v daném bodě
pro spojitou veličinu: $EX = \int_{-\infty}^{\infty} x f_{X}(x) dx$

Výpočet rozptylu

Rozptyl $DX=E((X-EX)^{2})$ udává, jak jsou hodnoty „daleko“ od střední hodnoty
udává se v jednotkách na druhou, zavedla se také výběrová směrodatná odchylka, která se rovná $\sqrt{DX}$ a udává hodnotu v jednotkách

Aby se dal rozptyl lépe spočítat, můžete využít alternativní vzorec: $DX = E(X^{2}) - (EX)^{2}$ , kde $E(X^{2})$ znamená, že do vzorce pro střední hodnotu $EX$ všude místo $X$ dáme $X^{2}$ , $(EX)^{2}$ je jen vypočítaná střední hodnota na druhou.

Výpočet kovariance a korelačního koeficientu

Kovariance

kovariance měří sílu lineární závislosti (jen lineární, jiné závislosti ne)
$cov(X,Y) = E(XY) - E(X)E(Y)$

Korelační koeficient

Korelační koeficient udává míru lineární závislosti, označuje se $\rho_{XY}$ a je to bezrozměrné číslo z intervalu $<-1,1>$
Pro $\rho = 1$ je mezi X,Y přímá lineární závislost. Pro $\rho = - 1$ je mezi X,Y nepřímá lineární závislost. Pro $\rho = 0$ jsou veličiny X,Y lineárně nezávislé, a říkáme o nich, že jsou nekorelované. Nulová hodnota koeficientu korelace tedy neznamená obecnou nezávislost obou veličin X a Y, ale pouze nezávislost lineární.⁴⁾
pro výpočet potřebuje kovarianci
$\rho_{XY} = \frac{cov(X, Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$

Příklad

Zadání: Nechť náhodné veličiny U,V mají diskrétní rozdělení určené následující tabulkou:

U\V	1	2	3
1	0,1	0,2	0,3
2	0,2	0,1	0,1

Najděte marginální rozdělení obou náhodných veličin, jejich střední hodnoty, rozptyly a korelační koeficient.

Řešení:
Nejprve si jen pro kontrolu můžete spočítat součet všech hodnot v tabulce, pokud je roven 1, je zadání spravné.
Do tabulky si přidáme marginální hodnoty – jsou to laicky řečeno projekce řádků a sloupců

U\V	1	2	3	P(U)
1	0,1	0,2	0,3	0,6
2	0,2	0,1	0,1	0,4
P(V)	0,3	0,3	0,4	1

Spočítáme si střední hodnoty E(V) a E(U) a hodnotu E(UV):

$E(U) = 1 \cdot 0,6 + 2 \cdot 0,4 = 1,4$

$E(V) = 1 \cdot 0,3 + 2 \cdot 0,3 + 3 \cdot 0,4 = 2,1$

$E(UV) = 1 \cdot 1 \cdot 0,1 + 1 \cdot 2 \cdot 0,2 + 1 \cdot 3 \cdot 0,3 + 2 \cdot 1 \cdot 0,2 + 2 \cdot 2 \cdot 0,1 + 2 \cdot 3 \cdot 0,1 = 2,8$
Spočítáme si rozptyl D(V) a D(U):

$D(U) = E(U^{2}) - (E(U))^{2} = (1^{2} \cdot 0,6 + 2^{2} \cdot 0,4) - (1,4)^{2} = 0,24$

$D(V) = E(V^{2}) - (E(V))^{2} = (1^{2} \cdot 0,3 + 2^{2} \cdot 0,3 + 3^{2} \cdot 0,4) - (2,1)^{2} = 0,69$
Spočítáme si kovarianci:

$cov (U,V) = E(UV)- E(U) \cdot E(V) = 2,8 - 1,4 \cdot 2,1 = -0,14$
Spočítáme si korelační koeficient:
$\rho_{uv} = \frac{cov(U,V)}{\sqrt{D(U)D(V)}} = \frac{-0,14}{\sqrt{0,24\cdot 0,69}} = -0,344$ (přibližně)

Důsledek: mezi veličinami U,V je spíše nepřímá lineární závislost. ⁵⁾

Zdroj

http://www.fi.muni.cz/~xhalic1/statnice/vypracovaneIM.doc http://www.math.muni.cz/~xpupik/dokumenty/pst-prednasky.pdf http://cs.wikipedia.org/wiki/Kovariance http://cs.wikipedia.org/wiki/Rozdělení_pravděpodobnosti http://cs.wikipedia.org/wiki/Pravděpodobnost

Informace trochu zorganizovala, opravila a doplnila Jitka Pospíšilová.

¹⁾ , ³⁾

převzato z http://cs.wikipedia.org/wiki/Pravděpodobnost

²⁾

příklad pochází z cvičení z předmětu MB104

⁴⁾

převzato z http://cs.wikipedia.org/wiki/Kovariance

⁵⁾

příklad převzat z domácích úkolů předmětu MB104

Diskuze

Jakub Talaš, 2008/05/30 15:25

Pravděpodobnost a statistiku jsem nikdy neměl rád a na její zpracování se fakt necítím :) ale aspoň nějaký základ jsem zkopíroval a malinko upravil od Eleny Halické. K této otázce se ještě nikdo nepřihlásil, tak aspoň torzo tu je pro ty, kteří by ji zpracovat chtěli nebo ty, co netuší, co od této otázky čekat.

JR, 2008/06/15 21:28

No to je fakt skareda otazka… Som z nej uplne uplne mimo (hlavne z tej statistiky.. nikto tomu nerozumie, koho poznam :-( )

Jitka Pospíšilová, 2008/06/18 00:50

prevedla jsem ty matematicke znaky do pluginu math – ale statistiku jsem se jeste nezacla ucit, takze jsem tomu zadnou vetsi informacni hodnotu nepridala, jsem si jen jista, ze jsem zadnou neubrala :) … behem dneska ci zitrka se zacnu ucit i statistiku podle mych zapisku z matiky, tak predelam ty zapisy, aby byly spravne (co budu vedet).

Jitka Pospíšilová, 2008/06/19 00:25

vsude jsem misto „velkeho Alfa“ (jevove pole) dala „velke Delta“ – velke Alfa se mi tady totiz nezobrazuje a mit tam jen pismenko A bylo hrozne matouci… jeste mam problem, ze se mi nezobrazuje binomicke cislo, to zatim nevim, jak vyresit.. je jen jedno, tak treba tam dam pak obrazek. Jinak vzorce jsem zatim jen prepsala podle skript pana Slovaka… zatim jim moc nerozumim, zvlast z tech skript, az se to budu ucit ze sesitu matiky, tak treba doplnim neco na pochopeni… a konec neni hotovy, protoze pan Slovak skripta nedokoncil, musim cerpat nekde jinde.

Jitka Pospíšilová, 2008/06/19 15:07

Věci, které jsem dala do modrých rámečků jsou buď příklady, nebo věci sloužící na pochopení. „To důležité“ by mělo být především v normálním textu otázky. Jen u rozdělení náhodných veličin si myslím, že je snad nemožné si ty všechny jednotlive funkce zapamatovat.

Jakub Talaš, 2008/06/20 15:08

Je z toho nakonec výborně zpracovaná otázka. Díky moc!

Peter Škoda, 2008/06/20 15:35

2 mini chybky su v casti „Rovnomerne rozdeleni“. f(t) je 0 ak je t>=b, F(t) je 1 ak je t>=b. Treba len otocit symboly mensie-vacsie. Myslim si, ze si kazdy sam tu chybku aj tak nasiel…

Michal Růžička, 2008/06/20 21:53

Dovolil bych si upozornit na zápisky z MB104 ze semestru jaro 2006. Konkrétně na zápisky z 5. (od strany 7), 6. (strana 1), 7. (strana 1–2, 4–9; geometrická pravděpodobnost v zadání této otázky není), 8., 9., 10. a 11. přednášky. Toto téma je tam myslím velmi pěkně vysvětleno.

Je tam pár „překlepů“ (psalo se to v dost svižným tempu), ale snad nic zásadního.

Marek Blahuš, 2008/06/21 13:03

Jestliže jev je prvkem jevového pole a to je systémem podmnožin základního prostoru, pak bych očekával, že i elementární jev, jakožto speciální případ jevu, bude jistou podmnožinou základního prostoru, a ne že bude přímo prvkem tohoto prostoru. Zápis {w} sedí, protože to je množina obsahující právě jeden možný výsledek, ale podle mne má tato množina být prvkem DELTA a nikoliv prvkem OMEGA (prvkem OMEGA je w samotné, nikoliv v množině). Opravte mne, pokud to špatně chápu, nebo opravte (či já opravím) článkem, pokud to chápu správně :-)

Jitka Pospíšilová, 2008/06/22 00:07

myslela jsem si, ze to celkem chapu, ale jak jsi to ted popsal, tak uz si tim vlastne nejsem jista. Kazdopadne cerpala jsem z tohoto dokumentu:
http://is.muni.cz/el/1433/jaro2007/MB104/um/matIV.pdf, konkretne strana 38. Opravuj otazku, jak uznas za vhodne.

Marek Blahuš, 2008/06/22 15:30

Díky za poukázání na zdroj. Myslím, že jsem po chvíli čtení pochopil, jak to prof. Slovák měl tehdy asi na mysli: Když nejprve píše, že celý základní prostor je jistý jev, tak pak elementární jev (taky jev) musí být intuitivně ten celý základní prostor bez něčeho. Tedy pokud víme, že elementární jev je jen nějaká jediná věc, tak pak to musí být celý základní prostor bez všech jeho prvků až na právě jeden. Pokud bychom celý základní prostor označili jako Omega = {omega_1, omega_2, …, omega_n}, pak elementární jev bude {omega_i} pro nějaké i \in {1, 2, …, n}. V materiálu použitý množinový tvar zápisu je tedy dobře, jen už není korektní to „patřítko“, protože prvkem množiny Omega není {omega}, nýbrž omega.

Myslím si, že to vzniklo jako jakási nevhodná zkratka od toho, že elementární jev je jednoprková množina, k tomu, že pro formální správnost nesmí být zapomenuto uvést, že omega je vybírána jako prvek z Omega (což ostatně sice nepřímo, ale velmi přesvědčivě potvrzuje jiná zmínka vztahu těchto proměnných v horní části téže stránky).

Opravil jsem tedy vypracování otázky v tom smyslu, že nikoliv elementární jev je {omega} náležící Omega, ale že elementární jev je {omega} a omega náleží Omega.

Marek Blahuš, 2008/06/21 13:15

K příkladu s Romeem a Julií: Má být funkce, kterou potřebujeme sestavit, skutečně v „prostoru“? To by musela mít tři vstupy, zatímco já si to dovedu představit snadno jako graf se dvěma osami, tedy v rovině.

Marek Blahuš, 2008/06/21 13:30

Aha, možná se tím myslel pravděpodobnostní prostor. Pak by ale bylo vhodné to v článku uvést jasněji.

Petr Koutný, 2008/06/21 17:12

Ad příklad s distribuční funkcí pro F(3): nemělo by to být jenom 2 * 1/6 namísto 3 * 1/6, protože se to určuje pro X < x a x = 3. Nebo se pletu? Trošku tápu, pokud mi někdo pomůže, tak budu rád.

Marek Blahuš, 2008/06/21 17:29

To stávající řešení odpovídá definici distribuční funkce jak je těsně nad tím rámečem. Ve Wikipedii (cs i en) je ale porovnávání v definici této funkce neostré, takže pokud to náhodou není nějaký zakořeněný zvyk na FI, který by bylo záhodno dodržovat, tak bych se spíš klonil k této asi uznávanější definici, a sice, že ta nerovnost má být neostrá, nikoli ostrá jako je tam teď. Ono nakonec pro nediskrétní náhodné veličiny je ta (ne)ostrost asi docela jedno, ale u těch diskrétních jako v tomto případě už to má docela význam.

Petr Koutný, 2008/06/21 21:48

Já mám právě v poznámkách ze cvičení ostrou…nicméně tohle je fakt asi detail, kterej nikdo řešit nebude, když víš, co to náhodná veličina je a co je to distribuční funkce :-)

Marek Blahuš, 2008/06/21 22:44

OK, i bych to opravil v textu, ale teď vidím, že by to tam asi způsobilo změny na mnoha místech, tak se do toho radši nechci pouštět. Nicméně tak, jak to tam je teď, je to taky nekonzistentní, jak správně poznamenal. Příklad s kostkou bych ale kvůli tomu neopravoval, protože by mi přišlo dost divné, kdyby se „plýtvalo“ na začátku a P(0) bylo totéž co P(1), zatímco jedničková pravděpodobnost by se získávala nejdříve až jako P(7). Tak to bude muset buď někdo projet a doplnit tam tu možnost rovnosti důkladně, nebo se to zatím nechá tak s tím, že tomu stejně každý už sám rozumí, jak to je :-)

Petr Koutný, 2008/06/22 07:40

Je to nesmysl něco upravovat, ostrá neostrá..o to nejde. Důležitý je vědět, co v té otázce je :-)

Jiri Schlemmer, 2008/06/25 21:40

Ahojte, nasel jsem chybku v binomickem rozdeleni, kde by (1-p)^1-t melo spravne byt (1-p)^n-t.
Dalsi chyba je v normalnim rozdeleni, kde hustota fX(x) neni …….e^x, ale …….e^((-x^2)/2).

Ondra Kozina, 2009/01/22 18:10

Je to tak, ze reseni prikladu na geometrickou pravdepodobnost je 5/18?

cele jmeno, 2009/01/31 21:03

je to 5/9

Jammo :), 2009/06/15 16:34

V tom priklade na binomicke rozdelenie by IMHO malo byt (n nad t) namiesto (n nad k)

Voštek Knyttr, 2009/06/19 10:18

Ten první jednoduchý příklad není zase tak jednoduchý. Ač to do toho autor nezaobalil, již tak se jedná o podmíněnou pravděpodobnost.

Petr Kadlec, 2009/06/20 16:28

Jen tak namatkove chyba je napriklad ve vzorci na Binomicke rozdeleni, ve vzorcich na hustotu a distrib. fci Normalniho rozdeleni. Spravne jsou vzorce treba na wikipedii.

Pavel Dvořák, 2009/06/23 16:18

Pokud uvidíš chybu, oprav ji prosím.

Petr Šigut, 2010/02/01 20:44

binomické rozdělení má být n-t, 1-t - snad po státnicích opravím, teď jsem jaksi na tom bídně s časem:)

You could leave a comment if you were logged in.

home/inf/ap12.txt · Poslední úprava: 2020/04/12 16:56 (upraveno mimo DokuWiki)

Nahoru