Obsah
12. Paralelní a distribuované systémy
Paralelní a distribuované systémy - základní pojmy a principy operací, koncept paralelních a distribuovaných algoritmů, řešení typových synchronizačních úloh (vzájemné vyloučení, volba vedoucího prvku, byzantská dohoda apod.) v paralelním a distribuovaném prostředí.
Vypracování
Základní pojmy a principy operací
Síťový model paralelních systémů
- Nezávislé procesy
- Navzájem si posílají zprávy
- Každý zná pouze svůj lokální pohled, přijímá a odesílá zprávy, ale nezná stav jiných procesů
- Zprávy se posílají asynchronně
- Důležitým vstupním údajem je topologie sítě, odpovídá neorientovanému grafu
Formálně se jedná o trojici , kde
je součin stavů všech procesů a zpráv na linkách, a běh systému je posloupnost
, kde
, tedy
je množina počátečních stavů.
Vzhledem k asynchronnosti nelze přesně měřit čas výpočtu. Pro měření složitosti se algoritmů se používají dva způsoby:
- Počet odeslaných zpráv
- čas běhu - počet kroků výpočtu měřený tzv. Lamportovými hodinami. Jako jeden krok se počítá vnitřní operace procesu, odeslání zprávy a přijetí zprávy.
Lamportovy hodiny
- pokud příjmu zprávu, přečtu příchozí hodnotu
, porovnám se svojí a vyšší nechám. Tu následně inkrementuji.
Řešení typových úloh
- Procesy se značí písmeny
- Algoritmy končí rozhodnutím, tj. operací Decide
- Samotný kód algoritmů tu přepisovat nebudu, jsou k dispozici v odkazovaných slidech
Prohledávání, traverzování
Prohledávání: Na začátku je jeden iniciátor a je třeba informovat všechny. Traverzování je stejná úloha, ale v každém okamžiku je jen jeden „token“, tedy jen jeden proces je aktivní.
f(x)-traverzování
Shout-and-echo
- Iniciátor pošle shout
- Když příjde shout do nového vrcholu:
- označ hranu, odkud shout přišel
- pošli do neoznačených shout
- počkej na echo od všech
- pak pošli echo zpět, odkud přišel první shout
- pokud příjde shout do již navštíveného vrcholu, okamžitě posílá echo
- Složitost:
- 4m zpráv - protože každý uzel pošle shout a echo, takže po každé hraně půjdou 4 zprávy
- 2diam(G) kroků
Prohledávání do hloubky (traverzování)
- Stručný popis algoritmu:
- Každý proces si do proměnné father uloží proces, od kterého poprvé přišel token, iniciátor tam uloží sám sebe
- každý proces si pamatuje, které hrany už byly „použité“ (used)
- Pokud proces příjme token poprvé, začnu ho posílat na ostatní porty. S každým odesláním tokenu označím port za použitý.
- Každý další příchozí token vrátím zpět odkud přišel a port opět označím jako použitý.
- Ve chvíli, kdy proces příjme token a všechny porty má označené jako použité, algoritmus končí (Decide). – k tomu dojde pouze na konci algoritmu v procesu iniciátora, nikde jinde!
- Složitost: 2m zpráv i kroků - protože po každé hraně jde „shout - echo“ jen jednou a nikdy se neposílají dvě zprávy v jeden čas.
Awerbuch - vylepšené prohl. do hloubky
- Podobné jako předchozí algoritmus
- Rozdíl je v tom, že při příjmu tokenu nejdříve odešlu všem uzlům <vis> zprávu a čekám na všechny odpovědi <ack>
- Pokud proces příjme <vis>, potvrdí příjem zprávou <ack> a označí daný port jako použitý
- Pokud potom do takového uzlu příjde token, uzel ho nebude přeposílat procesům, odkud už přišel <vis>
- Jinak řečeno, uzel posláním <vis> zpráv předejde tomu, že se mu po nějakém cyklu v grafu token vrátí
- Složitost: 4m zpráv, 4n - 2 kroků
Volba šéfa
Na úplných grafech - jednoduchý algoritmus
- Každý proces odešle všem ostatním zprávu se svým ID
- Když proces příjme zprávu s vyšším ID než má on sám, odpoví zprávou <accept>
- Pouze procesu s nejvyšším ID odpoví všechny ostatní procesy - tím pádem ví, že je leader a informuje o tom všechny ostatní
Na úplných grafech - pokročilý algoritmus
- Každý uzel prochází v cyklu všechny svoje sousedy a v každém průchodu:
- Odešle capture zprávu se svým levelem a ID
- Pokud mu proces odpoví accept, zvýší si level a pokračuje dalším průchodem cyklu (další sousední proces)
- Pokud příjmu caputre od procesu s vyšším levelem, nebo stejným levelem a vyšším ID - vrátím access
- Pokud příjmu caputre od procesu s nižším levelem a jsem ve stavu active nebo killed, nereaguji
- Pokud příjmu caputre od procesu s nižším levelem a jsem ve stavu captured, zeptám se „rodiče“, jestli má vyšší level
- Pokud ano nereaguj
- Pokud ne, pošli accept
- Složitost cca n.log n
Na jednosměrných kruzích (Chang Roberts)
- Každý proces pošle svoje ID po kruhu
- Pokud obdržím ID jiného procesu, přepošlu ho jen, pokud je nižší
- Pouze procesu s nejnižším ID se zpráva s jeho ID vrátí zpět.
- Takový proces je tedy leader a oznámí to zprávou <leader>
- Složitost
GHS
Konstruuje MST - (mininalni) kostru grafu.
- Vrcholy si pro každou hranu pamatují stav Basic, Branch, Rejected. Basic mají všichni na začátku, Rejected získávají ty hrany, které nepatří do MST, opačně pak Branch.
- Na začátku mají všichni level 0. Postupně se vrcholy spojují a zvyšují si level - tvoří fragmenty (les), aktualizují stav hran.
- To provádí cyklicky:
- Broadcast - jádro oznamuje všem ve fragmentu level fragmentu a ID jádra (iniciální hrana).
- ConvergeCast - vrcholy na hranicích fragmentu zjistí level sousedních fragmentů a vyšlou je dovnitř vlastního segmentu. Nějak se to vypropaguje až k jádru fragmentu. Tam se rozhodne, který nový fragment bude připojen.
- Change Core - info o připojení se přenese k požadovanému krajnímu uzlu, fragmenty se spojí a jedno jádro se zruší. Broadcast pak opět všem řekne, kdo je jádro.
- Spojení fragmentů: Merge, pokud oba mají stejnž lvl. Nový lvl = starý + 1. Jinak Absorb: nový lvl = větší ze starých levelů.
KKM
lecture03
Založeno na principu f(x)-traverzování, tokeny traverzují a nesou info o levelu. Kdyz se dva tokeny setkají, vznikne nový s vyšším lvl.
Počet zpráv = O(log_n(n + f(n)))
vzájemné vyloučení
Popis problému
- K určité kritické sekci může přistupovat jen jeden proces, je tedy třeba řešit přístup
- Algoritmy řešící vzájemné vyloučení musí splňovat tři podmínky:
- Vzájemné vyloučení - jen jeden proces může přistoupit do KS v daném čase
- Absence deadlocků - nikdy se nestane, že všechny procesy čekají a žádný nevstoupí do KS
- Procesy nehladoví - nikdy se nestane, že proces se v konečném čase nedostane do KS, protože jiné procesy tam vstupují před ním
Řešení pomocí tokenu
- V síti je vytvořen logický okruh, po kterém se posílá token
- Pouze proces s tokenem může vstoupit do KS
Ricart-Agrawala
- v systémů fungují logické hodiny
- Když chci do kritické sekce, pošlu
a čekám na odpovědi od všech
- Pokud někdo neodpovídá, tak
- buď je v kritické sekci
- nebo požádal o přístup dříve a také čeká
S použitím tokenu
- pro každý proces mám jeho poslední požadavek
- pro vstup: pošlu všem token a čekám na odpověď
- při opuštění: zjistím, kdo čekáa (v tokenu je tabulka posledních držení)
Byzantinská dohoda
Popis problému (Consensus problem)
- V synchronním paralelním systému jsou označené procesy a každý začíná s určitou hodnotou
- Systém obsahuje maximálně f zlých (byzantinských) procesů – mohou se chovat nejhorším možným způsobem, jako by znali aktuální stav všech ostatních procesů
- O co nám jde:
- Dohoda - Všechny dobré procesy se musí shodnout na stejné hodnotě
- Ukončení - každý proces se rozhodne v konečném čase
- Netrivialita - Pokud všichni dobří začnou se stejnou hodnotou i, musí s ní i skončit
- Integrita - Procesy se musí dohodout na hodnotě, kterou alespoň jeden proces navrhuje
Horní hranice chybných procesů
- Počet zlých procesů, se kterým je možné problém ještě vyřešit je
- Pokud je jich přesně třetina, pak se dá problém zobecnit na jeden z případů na obrázku níže:
- První a druhý případ - v prvním kole pošlou dobré procesy pravdivé údaje, zlý proces pošle opačné. Ve druhém kole pošle zlý proces opět nepravdivé údaje a tím zvrátí dohodnutou hodnotu.
- Třetí případ - zlý proces k simuluje pro proces j případ z obrázku (b) a pro proces i případ z obrázku (a), tím se oba procesy dohodnou na opačných hodnotách
algoritmus EIG
- lecture06
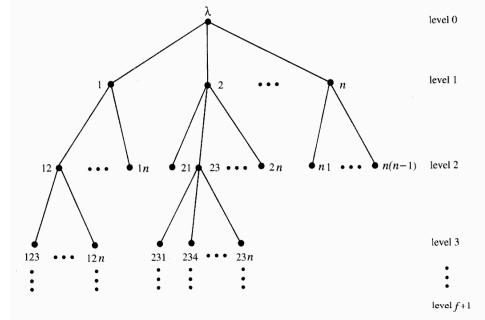
- Postupuje se v kolech, v každém kole pošle každý proces informace, které dostal v kole předchozím.
- Kolo1: Pošlu všem sousedům svoji hodnotu
- Kolo2: Pošlu všem sousedům hodnoty, které mi řekli, že mají mí sousedi.
- Kolo3: Pošlu všem sousedům hodnoty, o kterých mi sousedi řekli, že je mají jejich sousedi, atd…
- Kolo4: …
- Tímto způsobem si každý proces buduje strom (obrázek níže). V každém uzlu je uložena hodnota, která odpovídá dané posloupnosti. (
znamená, že proces i ví, že proces j ví, že proces k ví, že proces l má hodnotu 0)
- Také definujme hodnotu newval tak, že newval(x) je většina z newval(xj)
- Po f+1 kolech platí, že pokud i,j,k jsou dobré procesy, pak
pro všechny prefixy x
- Po f+1 kolech platí, že pokud je k dobrý proces, pak existuje hodnota v taková, že
pre všetky dobré procesy i
- Pokud začali všichni se stejnou hodnotou, už ve druhém kole se mohou dohodnout
- vrchol x je dobrý, pokud všechny dobré procesy i mají po f + 1 kolech newval(x)i = v pro nějaké v
- Po f + 1 kolech je na každé cestě z kořene do listu dobrý vrchol
- Po f + 1 kolech: pokud existuje pokrytí podstromu ve vrcholu x dobrými vrcholy, potom x je dobrý
Materiály
- Studijní materiály (slidy) jsou dostupné v ISu: https://is.muni.cz/auth/el/1433/podzim2009/IV100/um/
Vypracoval
Michal Trunečka
GHS: Marcel Poul



Diskuze
U té Byzantinské dohody musí být horní hranice počtu zlých procesů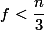 , pokud je zlých třetina nebo víc, tak už to není možné vyřešit podle důkazu.
, pokud je zlých třetina nebo víc, tak už to není možné vyřešit podle důkazu.